408 новая

20 мая 2022 г.

Тема: Решение тригонометрических уравнений; алгебраических относительно одной из тригонометрических функций.

При решении тригонометрических уравнений важную роль играет период тригонометрических функций.

Рекомендации по решению тригонометрических уравнений

1.     Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.

2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.

3.  Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.

4. Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.

5.  Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.

6.  Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.

7.  Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:

8.  Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. 

 Представьте в виде произведения:

Решение:

Используем формулы приведения, затем формулу преобразования суммы косинусов в произведение:

.

(На последнем шаге мы фактически использовали формулу двойного аргумента:

.

Ответ: .

Задание 2.

Вычислите:

Решение:

Воспользуемся формулой понижения степени и формулой преобразования произведения косинусов в сумму косинусов. Появившийся при этом общий множитель  вынесем за скобки:

Воспользуемся тем, что косинус – функция четная и известным значением косинуса. В результате получим:

Ответ: 0,25

Задание 3.

Проверьте равенство:

Решение:

При выполнении этого задания будем использовать прием домножения о деления левой части на одно и то же тригонометрическое выражение.

Но сначала заметим, что .

Теперь запишем левую часть: .

теперь домножим и разделим это выражение на : .

Теперь воспользуемся формулой синуса двойного аргумента и получим:

. Теперь еще раз воспользуемся формулой двойного аргумента, предварительно домножив числитель и знаменатель на 2:

Учитывая, что , получаем: .

То есть исходное равенство верно.

06 мая 2022 г.

Тема: Примеры использования арксинуса, арккосинуса, арктангенса числа.

Попробуйте вычислить значение выражения:

Решение:

В этом случае мы не можем воспользоваться тождеством, так как . Но в этом случае мы имеем табличные значения:

Ответ:

Задание

Вычислим значение выражения

Решение:

В этом случае мы также имеем табличные значения:

Ответ: 

1. Рассмотрим сначала задачи, связанные с вычислением табличных значений обратных тригонометрических функций.

Пример 1.

Найдите значение: .

Решение:

При решении данной задачи будем пользоваться табличными значениями аркфункций тождеством:

Ответ: .

Пример 2.

Вычислить: 

Решение:

На первый взгляд, использование тождества приводит к получению ответа:. Но заметим, что аргумент синуса не удовлетворяет промежутку . Поэтому ответ является неверным. Таким образом, нужно найти такое значение a , что:. Таким значением является . Значит, ответом является число .

2 вариант. Найдем численное значение . Оно равно . Теперь найдем . Оно равно.

Заметим, что второй вариант решения возможен в том случае, когда мы имеем дело с табличными значениями тригонометрических функций.

Ответ: .

Пример 3.

Вычислить: 

Решение:

В этом примере возможен только ход рассуждений по первому варианту, так как мы имеем дело не с табличными значениями косинуса. Очевидно, что число 10 не является правильным ответом, поскольку оно не принадлежит промежутку . Таким образом, нам нужно найти такое число a из промежутка , косинус которого равен косинусу 10. Таким значением a является число , так как значит,  и, с учетом формул приведения: .

Ответ: 1

Тождества, связывающие тригонометрические и обратные тригонометрические функции

и , если   и   и , если   и , если   и   и

. Рассмотрим некоторые тождества

С использованием тождеств, связывающих тригонометрические и обратные тригонометрические функции, рассмотрим решение некоторых примеров:

Пример 4.

Вычислите: .

Решение:

При решении этой задачи используется только знание табличных значений тригонометрических и обратных тригонометрических функций:

.

Ответ: 0.

Пример 5.

Вычислить: 

Решение:

Для вычисления значения данного выражения воспользуемся тождеством (22):

Ответ: -3

Пример 6.

Вычислить: 

Решение:

Сначала воспользуемся табличными значениями обратных тригонометрических функций и заменим . Теперь воспользуемся для преобразования формулой тангенса двух аргументов:

. Теперь, используя тождества для арктангенса и табличные значения тангенса, получим результат: 

Ответ: 

Решение задачи 2

Вычислить: .

Решение:

Данное выражение вообще не содержит табличных значений тригонометрических функций, поэтому при решении этой задачи будем использовать тождества второй группы. Но сначала воспользуемся формулой косинуса суммы аргументов. Таким образом, получим:

Ответ:.

Решение задачи 3

Вычислить 

Решение:

Воспользуемся для начала формулой синуса двойного аргумента и получим:

.

Теперь, используя тождества и преобразуя полученное выражение, получим окончательный результат:

Ответ: 

29 апреля 2022 г.

Тема: Простейшие тригонометрические неравенства.

Рассмотрим простейшие тригонометрические неравенства.

Начнем рассматривать с неравенства .

Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.

Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью

Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на  (получим неравенство , то решением его будет множество точек, в которых . Это числа .

Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью

Рассмотрим теперь значение  (рис.3).

Рисунок 3 – Решение неравенства 

Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1) , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением :

(для строгого неравенства) – множество интервалов;

(для нестрогого неравенства) – множество отрезков.

Если значение a= – 1,то получим следующую картинку (рис. 4):

Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью

Видно. что если неравенство нестрогое, то решением неравенства  является любое действительное число. Если неравенство строгое, то решением неравенства  является любое действительное число, кроме чисел вида .

Наконец, если , то решением неравенства  является любое действительное число.

Решение неравенства  рассмотрим более коротко.

Очевидно, что если , то решением неравенства  является любое действительное число.

Если , то решением неравенства  является любое действительное число, а решением неравенства  является любое действительное число, за исключением чисел вида .

Если , то решением неравенства  являются числа вида , а неравенство  решений не имеет. То же самое можно сказать о решении неравенств и  в случае .

Случай  рассмотрим более подробно (рис. 5).

Рисунок 5 – Решение неравенства 

Решение неравенства  для :

 (для строгого неравенства) - множество интервалов;

 (для нестрогого неравенства) - множество отрезков.

2. Теперь рассмотрим решение неравенств  и .

Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для  неравенство  решений не имеет, а решением неравенства  является любое действительное число.

Для  неравенство  решений не имеет, а решением неравенства  является любое действительное число.

Рассмотрим случай  более подробно.

Рассмотрим решение неравенства  (рис. 6).

Рисунок 6 – Решение неравенства 

Множество решений этого неравенства:

.

Теперь рассмотрим неравенство  (рис. 7).

Рисунок 7 – Решение неравенства 

Множество решений этого неравенства:

 .

3. Теперь рассмотрим решение простейших неравенств  и .

Сначала рассмотрим неравенство  (рис. 8).

Рисунок 8 – Решение неравенства 

Множество решений этого неравенства:

 .

Соответственно, множество решений неравенства :

 .

Пример 1.

Решите неравенство. Заполните пропуски

Решение:

Ведем новую переменную: .

Вспомогательное неравенство имеет вид:

 , .

Вернемся к исходной переменной: .

Второе неравенство решений не имеет. Решением первого неравенства является:

 .

Ответ:  .

Пример 2.

Решите неравенство. Найдите коэффициенты

Решение:

Выразим 

Рисунок 9 – решение неравенства 

Ответ: 

Тема: Арксинус, арккосинус, арктангенс числа.

При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.

Нахождение значения аргумента

Например, найдем все значения аргумента, при которых значение функции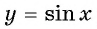 

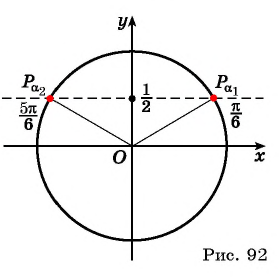
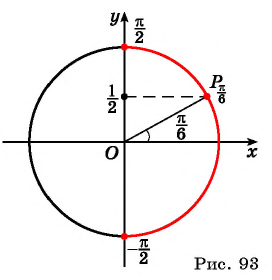
На единичной окружности найдем точки 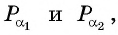 ординаты которых равны 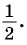Этим точкам соответствуют углы  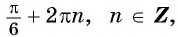 и 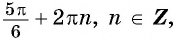и таких углов бесконечно много. Однако, если рассмотреть промежуток  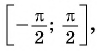то на нем функция  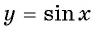возрастает и принимает все значения от -1 до 1. Поэтому для любого числа  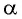из промежутка  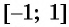существует единственное число  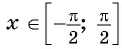такое что  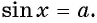Так на промежутке 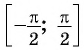существует единственное значение аргумента, при котором значение функции  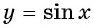равно 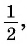 — это угол равный 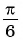( рис.93) 

Определение Арксинуса

Определение:

Арксинусом числа 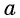 называется угол, принадлежащий промежутку  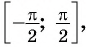синус которого равен  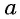(рис. 94).

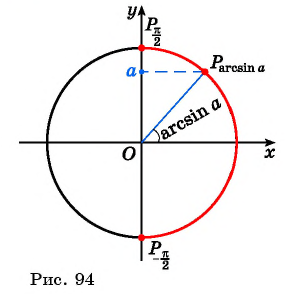
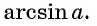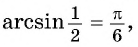Этот угол обозначают  Так,  поскольку  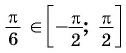и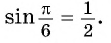 

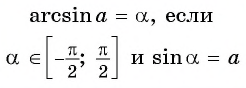
Пример №1

Вычислите:

Решение:

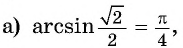   так как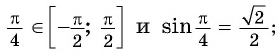 

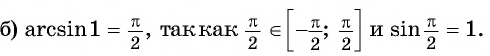
Пример №2

Найдите значение выражения:

Решение:

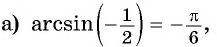  так как

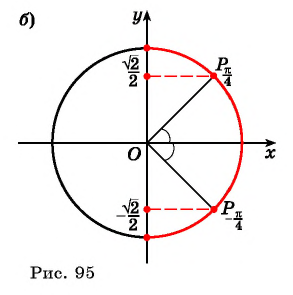
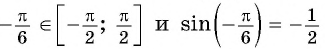 (рис. 95, б).

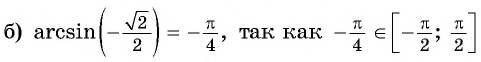
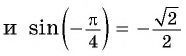
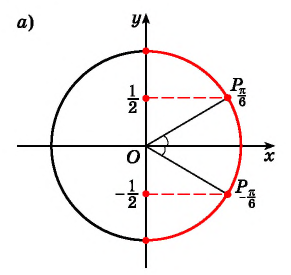
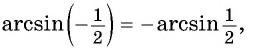
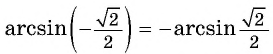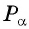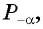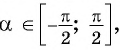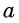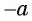Заметим, что  ( рис.95)  Так как углы, соответствующие точкам  и  где  с ординатами  и  отличаются только знаком, то  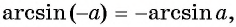для любого числа  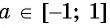(рис. 96).

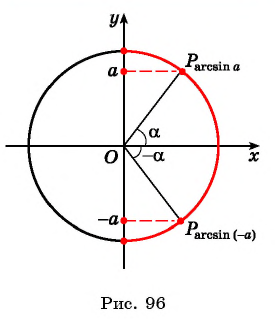
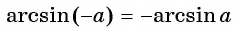
Пусть 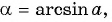 тогда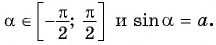 
Так как точки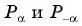 имеют противоположные ординаты, то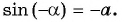 
Поскольку 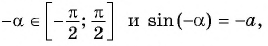 то по определению арксинуса  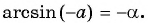Так как  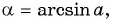то 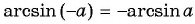 для любого числа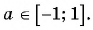 
Воспользуемся полученным равенством и найдем значение выражения

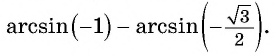
Так как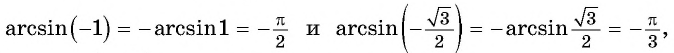 

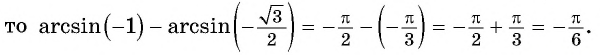
Отметим, что областью определения выражения 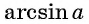 является отрезок  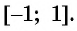Если 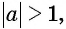 то выражение  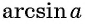не имеет смысла.

Например, выражения 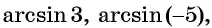 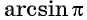 не имеют смысла, так как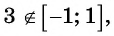 
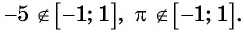
Выражение 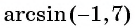 не имеет смысла, так как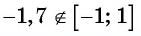 
Из определения арксинуса числа следует, что 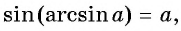 если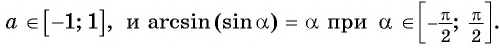 

Например,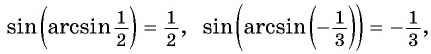 

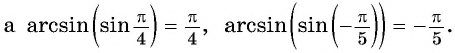
Рассмотрим промежуток 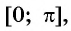 на котором функция  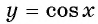возрастает и принимает все значения от  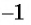до 1. Для любого числа  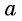из промежутка  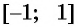существует единственное число  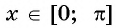такое, что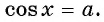 

Определение Арккосинуса

Определение:

Арккосинусом числа 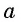 называется угол, принадлежащий промежутку  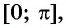косинус которого равен  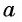(рис. 97).

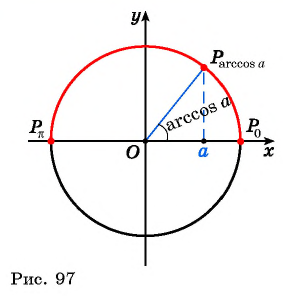
Этот угол обозначают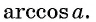 

Например: 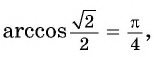 поскольку  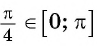и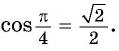 
 

Пример №3

Вычислите:

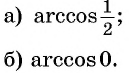
Решение:

 

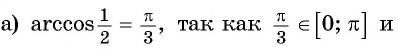
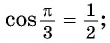
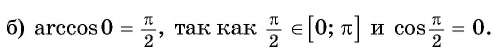
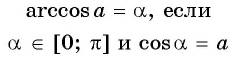
Пример №4

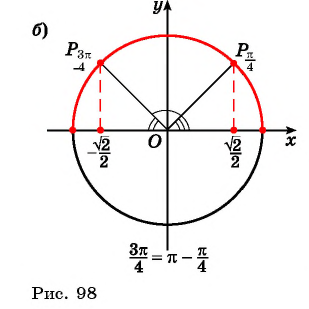
Найдите значение выражения:

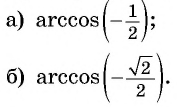
Решение:

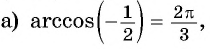  так как  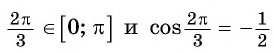( рис. 98.а)

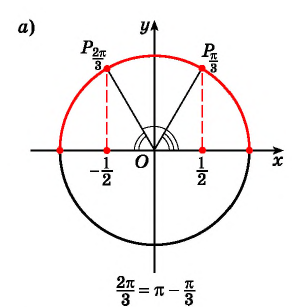
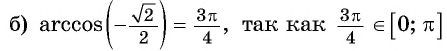
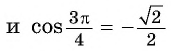 ( рис.98.б)

Заметим, что 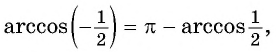 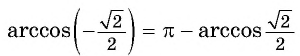( см.98) 

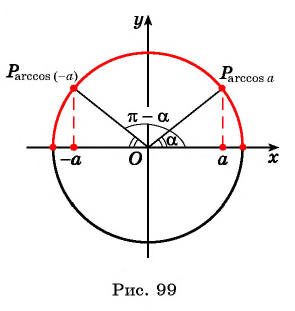
Пусть 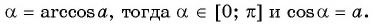 Так как точки  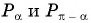имеют противоположные абсциссы, то  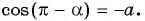Поскольку  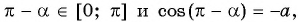то по определению арккосинуса  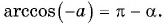Так как  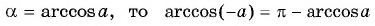для любого числа  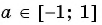(рис. 99).

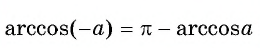
Воспользуемся полученным равенством и найдем значение выражения

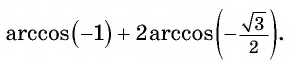
Так как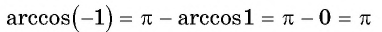 
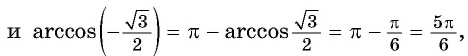
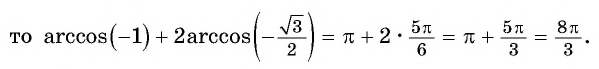
Областью определения выражения 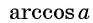  является отрезок  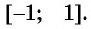Если 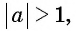 то выражение  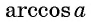не имеет смысла.

Так, выражения 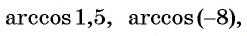 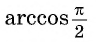не имеют смысла, поскольку

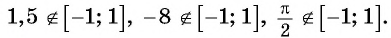
Выражение 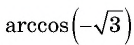 не имеет смысла, так как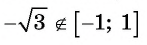 
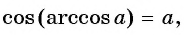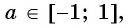Из определения арккосинуса числа следует, что  если  и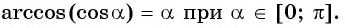 

Например,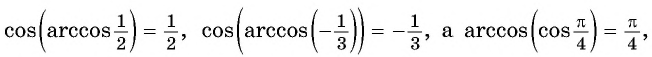 

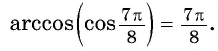
На промежутке монотонности 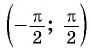 функции  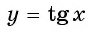существует единственный угол, тангенс которого равен некоторому данному числу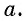 

Определение Арктангенса

Определение:

Арктангенсом числа 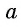 называется угол, принадлежащий промежутку  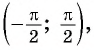тангенс которого равен  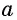(рис. 100).

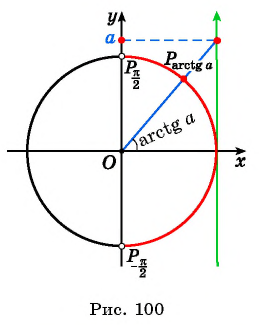
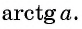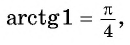Этот угол обозначают  Так,  поскольку  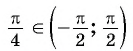и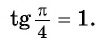 

Пример №5

Вычислите:

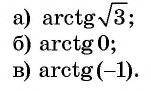
Решение:

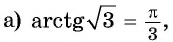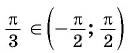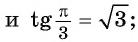
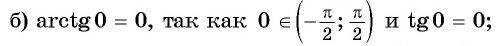
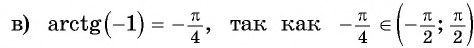  так как  и 

 и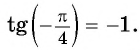 

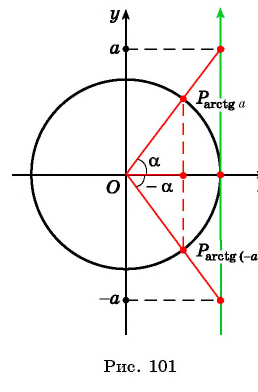
Для любого числа 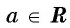 верно равенство  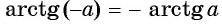(рис. 101).

 

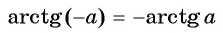
Пример №6

Найдите значение выражения

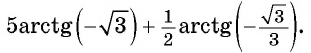
Решение:

Так как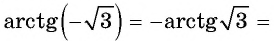 
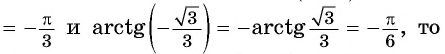
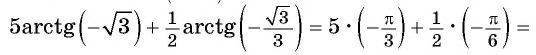
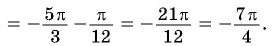
Из определения арктангенса числа следует, что 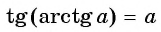 при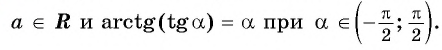 

Например,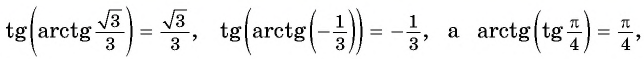 

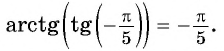
На промежутке монотонности 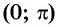 функции  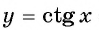существует единственный угол, котангенс которого равен некоторому данному числу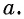 

Определение Арккотангенса

Определение:

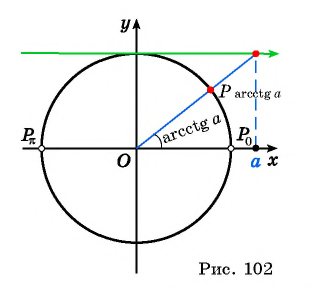
Арккотангенсом числа 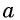 называется угол, принадлежащий промежутку  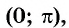котангенс которого равен  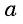(рис. 102).

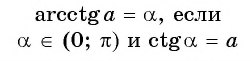
Этот угол обозначают 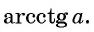 Например,  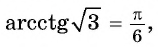поскольку

• Заказать решение задач по высшей математике

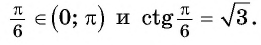
Пример №7

Вычислите:

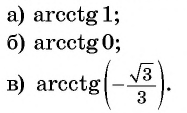
Решение:

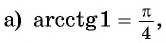 так как

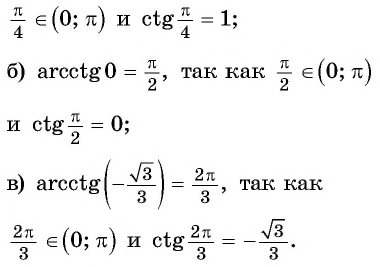
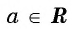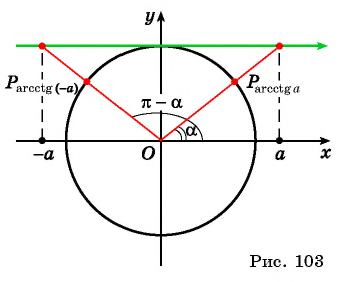
Для любого числа  верно равенство 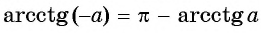 (рис. 103).

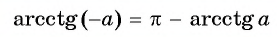
Пример №8

Найдите значение выражения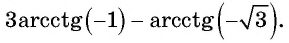 

Решение:

Так как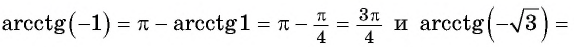 

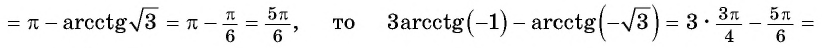
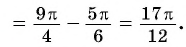
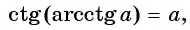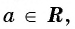Из определения арккотангенса числа следует, что  если  и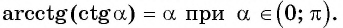 

Например,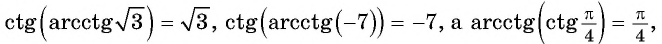 

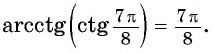
Примеры заданий и их решения

Пример №9

Верно ли, что:

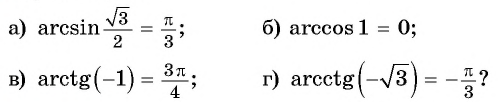
Решение:

а) Верно, так как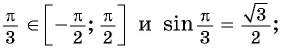 

б)    верно, так как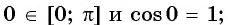 

в)    неверно, так как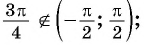 

г)    неверно, так как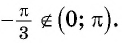 

Пример №10

Вычислите:

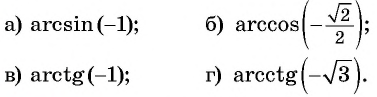
Решение:

 

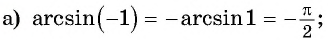
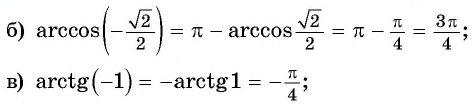
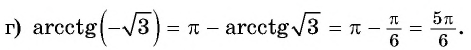
Пример №11

Найдите значение выражения:

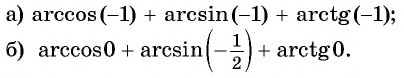
Решение:

 

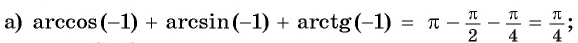
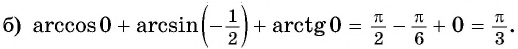
Пример №12

Оцените значение выражения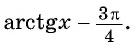 

Решение:

По определению арктангенса числа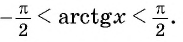 

Воспользуемся свойствами числовых неравенств и получим: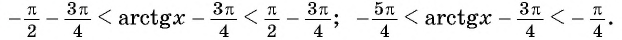 

Пример №13

Найдите область определения выражения:

Решение:

 а) По определению арксинуса числа 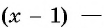 это угол, синус которого равен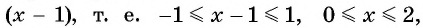 

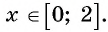
б)    По определению арккосинуса числа 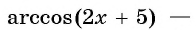 это угол, косинус которого равен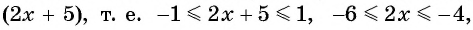 

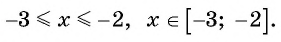
Пример №14

Найдите значение выражения:

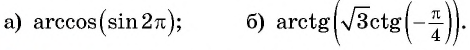
Решение:

 

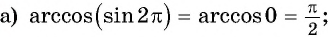
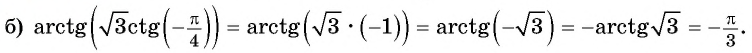
Пример №15

Вычислите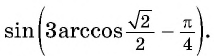 

Решение:

 

22 апреля 2022 г.

Тема: Простейшие тригонометрические уравнения.

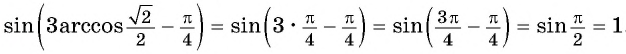
Определение . Равенство тригонометрических выражений , содержащих неизвестное только под знаком тригонометрических функций называется тригонометрическим уравнением .

sin x = a

Если а > 1 , то уравнение sin x = a не имеет решений , так как sin x  1 для любого х . Отложим на оси ординат а – значение синуса. Этому значению на единичной окружности соответствуют точки  и , причём  .

На этом отрезке функция синус возрастает и уравнение sin x = a имеет единственный корень

х₁ = arcsin a.

На отрезке  функция синус убывает и принимает все значения от – 1 до 1 . По теореме о корне уравнение имеет один корень x₂ =  - arcsin a /

Итак , с учётом периодичности уравнение sin x = a имеет два решения

х₁ = arcsin a + 2n, n  Z

x₂ =  - arcsin a + 2n , n  Z .

Удобно записывать эти оба решения одной формулой :

х =(-1)^k arcsin a + k, k  Z .

Если k = 2n , то х₁ = arcsin a + 2pn, n Î Z .

Если k = 2n + 1 ,то x₂ =  - arcsin a + 2n , n  Z .

При изучении свойств функции у = sin x мы находили путём логических рассуждений нули функции из условия sin x = 0 , экстремальные точки из условия sin x = 1 и sin x = - 1 . Фактически мы находили корни особых случаев решения уравнения sin x = а .

Они имели вид :

sin x = 0 х = n, n  Z .

sin x = 1 х = + 2pn, n Î Z .

sin x = -1 х = -+ 2pn, n Î Z .

Примеры

1. sin x = 

х =(-1)^k arcsin  + k, k  Z .

так как arcsin =  , то

х =(-1)^k  + k, k  Z .

2. sin 2x = – 

2х =(-1)^k arcsin  + k, k  Z .

так как arcsin = - arcsin = -  , то

2х =(-1)^k+1  + k, k  Z .

х =(-1)^k+1  + , k  Z .

II. cos x = a

Если а > 1 , то уравнение cos x = a не имеет решений , так как  cos x   1 для любого х . Пусть  а   1 . Надо найти все такие числа х , для которых cos x = a . На отрезке  существует одно такое решение – это арккосинус числа а.

Косинус чётная функция , и , значит , на отрезке уравнение имеет в точности одно решение , это число - arccos a.

Итак, уравнение cos x = a на отрезке  длиной 2 имеет два решения :

х₁ = arccos a ,

х₂= - arccos a.

Вследствие периодичности функции косинус все остальные решения отличаются от этих на 2n , n Z и объединяются в одну формулу :

х =  arccos a + 2n , n Z .

Решение уравнения можно проиллюстрировать на единичной окружности .

По определению cos x – это абсцисса точки Р_х единичной окружности . Если а < 1 , то таких точек две ; если же а = 1 или а = - 1 , то одна .

При а = 1 числа arccos a и - arccos a совпадают ( они равны нулю ) , поэтому решением уравнения cos x=1 будет х = 2 n , n Z .

При а = - 1 имеем : cos x= -1 х =  + 2 n , n Z .

При а = 0 имеем : cos x= 0 х = +  n , n Z .

Примеры :

1. cos x= 

х =  arccos  + 2p n , nΠZ .

так как arccos =  , то

х =   + 2p n , nΠZ .

Ответ :   + 2p n , nΠZ .

3. tg x = a

При любом а на интервале имеется только одно значение х , такое число х , что tg x = a - это arctg a.

Поэтому уравнение tg x = a на интервале имеет единственный корень . Функция у = tg x периодическая , её наименьший период . Следовательно , остальные корни отличаются от найденного на n ,

х = arctg a + n , nΠZ .

15 апреля 2022 г.

Тема: Тождественные преобразования тригонометрических выражений.  Преобразование простейших тригонометрических выражений.

Основные формулы тригонометрии

Перевод градусной меры угла в радианную и обратно.

Пусть α — градусная мера угла, β — радианная, тогда справедливы формулы:

Формулы зависимости между функциями одного и того же аргумента:

Формулы сложения.

Формулы двойных и половинных углов.

Формулы преобразования суммы в произведение:

Формулы преобразования произведения в сумму:

Формулы приведения:

Рассмотрим сначала достаточно простые задания на применение формул тригонометрии.

Пример 1.

Вычислить значение sin α, если cos α = 0,3, α — угол в первой четверти.

Решение:

Применим основное тригонометрическое тождество, связывающее тригонометрические

функции .

Решая уравнение sin2α = 0,91, получаем два случая (), из которых, обращая внимание на то, какой четверти принадлежит искомый угол, следует выбрать один. Вспомним, что в первой четверти все тригонометрические функции имеют знак «+». Следовательно, .

Ответ: .

Пример 2.

Решение:

Ответ: 5.

Пример 3.

Упростите выражения:

Пример 4.

Вычислите:

Отдельную группу заданий этого типа составляют задания на вычисление одних тригонометрических функций по известным другим.

Пример 5.

Известно, что sin α – cos α = 0,3. Найти:

Решение

1) Возведем в квадрат обе части заданного в условии примера равенства и используем формулу «квадрат разности», получаем, что:

Вспомним основное тригонометрическое тождество и применим формулу синуса двойного угла:

2) Воспользуемся полученным результатом для ответа на вопрос 2.

Комментарий. Специальный вид, использованный при решении данного примера, позволяет применить формулу «квадрат суммы» и использовать результат, полученный в пункте 1. При последующих преобразованиях использована формула синуса двойного угла.

3) Обратим внимание, что для вычисления значения выражение sin6α + cos6α можно представить в виде суммы кубов.

Ответ:

Тема:  Преобразование простейших тригонометрических выражений.

8 апреля 2022 г.

Тема: Преобразование суммы тригонометрических функций в произведение. Преобразование произведения тригонометрических функций в сумму.

1. Формулы для преобразования произведения синуса и косинуса в сумму, получаются из формул сложения для синуса и косинуса. Запишем формулы для синуса суммы и синуса разности углов

Сложив почленно эти равенства и разделив результат на 2 получим:

sin() + sin() = 2 sin cos получаем:

2. Запишем формулы для косинуса суммы и косинуса разности углов :

Сложив почленно эти равенства и разделив результат на 2 получим:

3. Аналогично, вычитая из второго равенства первое, в результате получаем:

4. Формулы преобразования произведения тангенсов и котангенсов в сумму:

Формулы суммы и разности 2-х углов

2 апреля 2022 г.

Тема: Синус и косинус двойного угла.

    Преобразования тригонометрических выражений можно упростить, если рассмотреть частные случаи общих формул. Рассмотрим формулу синуса суммы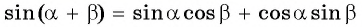 

Формула синуса двойного аргумента

Получили формулу синуса двойного аргумента: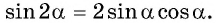 

Выведем формулу косинуса двойного аргумента. Используем формулу косинуса суммы 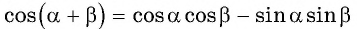 для случая  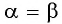и получим:

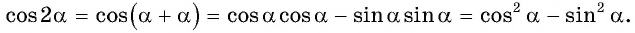
Формула косинуса двойного аргумента

Формула косинуса двойного аргумента: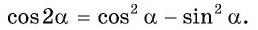 

Для вывода формулы тангенса двойного аргумента рассмотрим формулу тангенса суммы 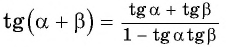 при 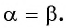 В этом случае имеем: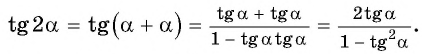

Формула тангенса двойного аргумента

Получили формулу тангенса двойного аргумента: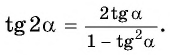 

Пример №1

Упростите выражение:

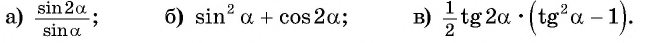
Решение:

Применим формулы двойного аргумента:

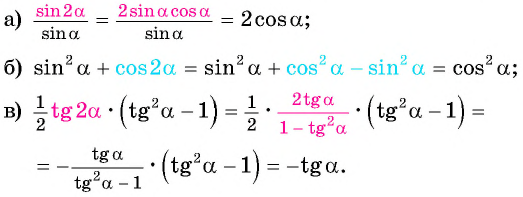
Пример №2

Вычислите:

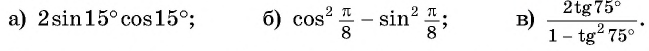
Решение:

Применим формулы двойного аргумента «справа налево»:

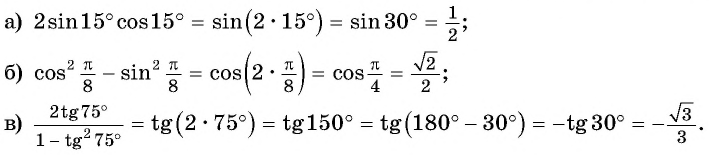
Пример №3

Найдите значение выражения 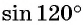 двумя способами.

Решение:

Первый способ. Применим формулы приведения:

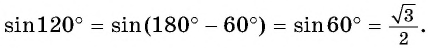
Второй способ. Применим формулу синуса двойного аргумента:

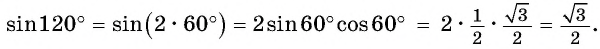
Пример №4

Представьте данный угол в виде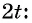 

Решение:

Тема: Формулы половинного угла. Решение примеров.

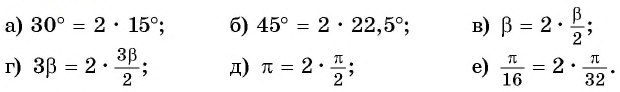
Список всех формул половинного угла

Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:

$\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}$
$\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$
$tg\frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}=$ $\frac{\sin \alpha }{1+\cos \alpha }=\frac{1-\cos \alpha }{\sin \alpha }$
$ctg\frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{1-\cos \alpha }}=$ $\frac{\sin \alpha }{1-\cos \alpha }=\frac{1+\cos \alpha }{\sin \alpha }$

Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол $\frac{\alpha }{2}$.

Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:

${\sin }^2\frac{\alpha }{2}=\frac{1-\cos \alpha }{2}$
${\cos }^2\frac{\alpha }{2}=\frac{1+\cos \alpha }{2}$
$t{g}^2\frac{\alpha }{2}=\frac{1-\cos \alpha }{1+\cos \alpha }$
$ct{g}^2\frac{\alpha }{2}=\frac{1+\cos \alpha }{1-\cos \alpha }$

Формула синуса и косинуса половинного угла имеет место при любом угле $\alpha$.

Формула тангенса половинного угла справедлива для тех углов $\alpha$, при которых определен $tg\frac{\alpha }{2}$, то есть при $\alpha \ne \pi +2\pi n,n\in Z$.

Формула котангенса выполняется для тех $\alpha$, при которых определен $ctg\frac{\alpha }{2}$, то есть при $\alpha \ne 2\pi n,n\in Z$.

С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла $\alpha$ через тангенс половинного угла.

$\sin \alpha =\frac{2tg\frac{\alpha }{2}}{1+t{g}^2\frac{\alpha }{2}},$ $\alpha \ne \pi +2\pi n,n\in Z$
$\cos \alpha =\frac{1—t{g}^2\frac{\alpha }{2}}{1+t{g}^2\frac{\alpha }{2}},$ $\alpha \ne \pi +2\pi n,n\in Z$
$tg\alpha =\frac{2tg\frac{\alpha }{2}}{1—t{g}^2\frac{\alpha }{2}},$ $\alpha \ne \pi +2\pi n,n\in Z,$ $\alpha \ne \frac{\pi }{2}+\pi n,n\in Z$
$ctg\alpha =\frac{1—t{g}^2\frac{\alpha }{2}}{2tg\frac{\alpha }{2}},$ $\alpha \ne \pi n,n\in Z,$ $\alpha \ne \pi +2\pi n,n\in Z$

Вывод формул половинного угла

Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла $\cos 2\alpha =1-2{\sin }^2\alpha$ и $\cos 2\alpha =2{\cos }^2\alpha -1$. Запишем их в следующем виде: $\cos \alpha =1-2{\sin }^2\frac{\alpha }{2}$ и $\cos \alpha =2{\cos }^2\frac{\alpha }{2}-1$. Выразив из первого равенства $\sin \frac{\alpha }{2}$ получим $\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}$. Аналогично разрешив второе равенство относительно $\cos \frac{\alpha }{2}$ в результате будем иметь $\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$.

Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде $tg\frac{\alpha }{2}=\frac{\sin \frac{\alpha }{2}}{\cos \frac{\alpha }{2}}$ и $ctg\frac{\alpha }{2}=\frac{\cos \frac{\alpha }{2}}{\sin \frac{\alpha }{2}}$, а также две уже доказанные выше формулы для синуса и косинуса.

В результате будем иметь: $tg\frac{\alpha }{2}=\frac{\sin \frac{\alpha }{2}}{\cos \frac{\alpha }{2}}=$ $\frac{\pm \sqrt{\frac{1-\cos \alpha }{2}}}{\pm \sqrt{\frac{1+\cos \alpha }{2}}}=$ $\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}$ и $ctg\frac{\alpha }{2}=\frac{\cos \frac{\alpha }{2}}{\sin \frac{\alpha }{2}}=$ $\frac{\pm \sqrt{\frac{1+\cos \alpha }{2}}}{\pm \sqrt{\frac{1-\cos \alpha }{2}}}=$ $\pm \sqrt{\frac{1+\cos \alpha }{1-\cos \alpha }}$.

Примеры использования при решении задач

Пример 1. Найти ${\cos 15}^{\circ }$, если известно, что ${\cos 30}^{\circ }=\frac{\sqrt{3}}{2}$.

Решение. Формула половинного угла для тригонометрической функции косинус имеет вид ${\cos }^2\frac{\alpha }{2}=\frac{1+\cos \alpha }{2}$. Подставив известные значения, имеем ${\cos }^2{15}^{\circ }=\frac{1+{\cos 30}^{\circ }}{2}=$ $\frac{1+\frac{\sqrt{3}}{2}}{2}=\frac{2+\sqrt{3}}{4}$. Имея значение ${\cos }^2{15}^{\circ }$, найдем ${\cos 15}^{\circ }$. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то ${\cos 15}^{\circ }=\sqrt{\frac{2+\sqrt{3}}{4}}=$ $\frac{\sqrt{2+\sqrt{3}}}{2}$.

Ответ. ${\cos 15}^{\circ }=\frac{\sqrt{2+\sqrt{3}}}{2}$.

Пример 2. Вычислить значение выражения $4\cos \frac{\alpha }{2}+2\cos \alpha +5$, если $\cos \alpha =\frac{1}{8}$.

Решение. Используя ту же формулу, что и в первом примере ($\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$) и известное значение косинуса, упростим выражение: $4\sqrt{\frac{1+\cos \alpha }{2}}+2\cos \alpha +5=4\sqrt{\frac{1+\frac{1}{8}}{2}}+2\cdot \frac{1}{8}+5=$ $4\sqrt{\frac{9}{16}}+\frac{1}{4}+5=8\frac{1}{4}$.

Ответ. $4\cos \frac{\alpha }{2}+2\cos \alpha +5=8\frac{1}{4}$.

1 апреля 2022 г.

Тема: Синус, косинус и тангенс суммы и разности двух углов.

Существуют основные формулы суммы и разности аргументов тригонометрических функций:

Если произвольный аргумент тригонометрической функции можно записать в виде произведения некоторого угла на 2, то для таких углов можно использовать формулы двойного угла.

Итак, давайте воспользуемся некоторой формулой для суммы аргументов:

А теперь давайте предположим, что углы α и β равны, то получим cos (2 β) = cos2 β - sin2 β.

Если данное предположение мы сделаем относительно синуса, то получим:

Если сделать аналогичные преобразования, то можно получить:

Все перечисленные формулы применимы для двойного аргумента.

19 марта 2022 г.

Тема: Формулы приведения. Решение упражнений.

Формулами приведения называются формулы, позволяющие тригонометрические функции углов    и  выражать через тригонометрические функции угла .

Мнемонические правила:

1. Если угол  отсчитывается от концов горизонтального диаметра 0; ± π;± 2π, то наименование функции не меняется; если угол  отсчитывается от концов вертикального диаметра ; , то наименование функции меняется на кофункцию (sin на cos, cos на sin, tg на ctg и ctg на tg).

2. Знак правой части определяется по знаку приводимой функции, стоящей слева.

При решении примеров применяются мнемонические правила формул приведения, свойства четности и нечетности и периодичности тригонометрических функций.

Свойства четности и нечетности: ; ; ; .

Свойства периодичности:; ; ; , где ÎZ.

Значения тригонометрических функций основных углов

Угол	0o 0	30o	45o	60o	90o	120o	135o	150o	180o π
Функция
	0				1				0
	1				0			–	–1
	0		1		–		–1		0
	–		1		0		–1		–

Пример 1. Вычислите .

Решение: применяя свойство периодичности и формулы приведения, получим: 

Пример 2. Вычислите .

Решение: воспользуемся свойством нечетности, периодичности и формулами приведения, получим:

Пример 3. Вычислите 

Решение:

== = =

–===.

Пример 4. Докажите тождество 

Решение:

.

Пример 5.

Упростите выражение: а) ;

б) .

Решение: а) используя формулы приведения, получим

.

б) 

Тема: Вычисление значений тригонометрических функций.

1. Определение тригонометрических функций для угла прямоугольного треугольника

    В прямоугольном треугольнике один из острых углов обозначим через α. Катет, противолежащий этому углу, назовем а; прилежащий катет – b, а гипотенузу – с.
    Существует шесть отношений сторон прямоугольного треугольника относительно фиксированного угла α, каждое из которых, соответственно, назвали:
    .
    Рассмотрим «тригонометрический ряд»:
                                                            . 
    Нетрудно заметить, что произведения тригонометрических функций равноотстоящих от концов «тригонометрического ряда», равны 1:
                                                        .
    Из теоремы Пифагора следует:
                                                         
    – основное тригонометрическое тождество или, как ещё его называют, «тригонометрическая единица».
    Если тождество   почленно разделить на  или на , то получим ещё два тождества:
    .
    Полученные шесть наиболее важных тригонометрических тождеств позволяют отыскать любую из тригонометрических функций при условии, что одна из шести будет известна.

2. Значения тригонометрических функций 30, 45 и 60 градусов

Рассмотрим равносторонний треугольник со стороной, равной 1. Высота этого треугольника равна   и делит сторону пополам.
    Из левого прямоугольного треугольника найдём: 

    .
    Т.к. , а , то
    .

    Из прямоугольного равнобедренного треугольника с гипотенузой, равной 1 и острыми углами по 45⁰ найдём:
        .

    Сведём все полученные результаты в таблицу:
                                                                                    

3. Определение тригонометрических функций на единичной окружности

    Величина угла α для прямоугольного треугольника находится в пределах от 0⁰ до 90⁰ градусов. Необходимо определить тригонометрические функции для других углов. Для этого рассмотрим окружность с радиусом, равным 1, и центром в начале декартовой системы координат. Зададим подвижный радиус OP, первоначальное, «нулевое» положение которого совпадает с положительным направлением оси OX, и вращение против часовой стрелки увеличивает величину угла, а вращение по часовой стрелке величину угла уменьшает. Если точка P лежит в первой четверти, то, рассматривая прямоугольный треугольник с гипотенузой 1 (т.к. радиус окружности равен 1) и острым углом α, получим: , где х, у – координаты точки Р – конца подвижного радиуса. Этими же соотношениями определяются тригонометрические функции углов меньше 0⁰ и больше 90⁰.

    Из определения тригонометрических функций вытекают важные их свойства:
    1. Все тригонометрические функции периодические. Причём sinα и cosα имеют наименьший (главный) период Т = 2π и общий период 2πk, где k – любое целое число. У tgα и ctgα наименьший период равен π, а общий πk, где k – целое число.
    2. sinα, tgα и ctgα – нечётные функции; т.е.
        sin (– α) = – sinα, tg (– α) = – tgα, ctg (– α) = – ctgα;
        cosα – чётная функция, т.е. cos (– α ) = cosα;
    3. Знаки тригонометрических функций:
        I четверть – положительны sinα, cosα, tgα, ctgα;
        II четверть – положителен только sinα, отрицательны cosα, tgα, ctgα;
        III четверть – положительны tgα, ctgα, отрицательны sinα, cosα;
        IX четверть – положителен cosα, а sinα, tgα, ctgα – отрицательны. 

    

    Важное значение при вычислении значений тригонометрических функций имеют формулы приведения, позволяющие свести аргумент тригонометрической функции к углу от 0⁰ до 90⁰. 
    Из рисунка видно, что относительно горизонтального диаметра наименование тригонометрической функции не меняется, а относительно вертикального меняется на кофункцию (синус на косинус, тангенс на котангенс и обратно).
    Для лучшего запоминания формул приведения можно воспользоваться мнемоническим правилом. Пусть  и α- угловые величины дуг единичной окружности, причём . Для того чтобы привести тригонометрическую функцию числа к тригонометрической функции числа α, необходимо:
    1) величину  представить в одном из следующих видов:

        
    2) сохранить наименование функции, если дуга величиной α откладывается от горизонтального диаметра  изменить наименование функции на кофункцию (синус на косинус, тангенс на котангенс и обратно), если дуга величиной  откладывается от вертикального диаметра  (см. «Правило носа» ).
    3) установить, в какой четверти расположен конец дуги величиной , и определить знак приводимой тригонометрической функции; этот же знак поставить перед значением приведённой функции.
     «Правило носа». Задайте вопрос: «Функция меняет имя?» и носом водите вдоль той оси координат, от которой откладывается острый угол α.

• по оси ОY носом водите вверх-вниз, что на мнемоническом языке означает «да» – значит, функция меняет своё имя на кофункцию;
• по оси OX носом водите влево-вправо, что на мнемоническом языке означает «нет» – функция имени не меняет.

Для выполнения тождественных преобразований необходимо знать следующие формулы:
    1.Формулы сложения
    .
    2.Формулы двойного аргумента
    .
    3.Формулы половинного аргумента
    .
    4.Формулы понижения степени

    

    5.Формулы преобразования суммы в произведения
    

    6.Формулы преобразования произведений в суммы
     .
    7. Определения обратных тригонометрических функций
     .

    8. Тригонометрические уравнения
    

18 марта 2022 г.

Тема: Основные тригонометрические тождества.

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

$\sin^{2}\alpha + \cos^{2} \alpha = 1$

$tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}$

$tg \alpha \cdot ctg \alpha = 1$

Зависимость между синусом и косинусом

$\sin^{2} \alpha+\cos^{2} \alpha=1$

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

$tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\frac{\cos \alpha}{\sin \alpha}$

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению $\displaystyle \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha}$, а отношение $\displaystyle \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha}$ — будет являться котангенсом.

Добавим, что только для таких углов $\alpha$, при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества $\displaystyle tg \alpha = \frac{\sin \alpha}{\cos \alpha}$, $\displaystyle ctg \alpha=\frac{\cos \alpha}{\sin \alpha}$.

Например: $\displaystyle tg \alpha = \frac{\sin \alpha}{\cos \alpha}$ является справедливой для углов $\alpha$, которые отличны от $\displaystyle \frac{\pi}{2}+\pi z$, а $\displaystyle ctg \alpha=\frac{\cos \alpha}{\sin \alpha}$ — для угла $\alpha$, отличного от $\pi z$, z — является целым числом.

Зависимость между тангенсом и котангенсом

$tg \alpha \cdot ctg \alpha=1$

Данное тождество справедливо только для таких углов $\alpha$, которые отличны от $\displaystyle \frac{\pi}{2} z$. Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что $\displaystyle tg \alpha = \frac{y}{x}$, а $\displaystyle ctg \alpha=\frac{x}{y}$. Отсюда следует, что $\displaystyle tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1$. Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

$\displaystyle tg^{2} \alpha + 1=\frac{1}{\cos^{2} \alpha}$ — сумма квадрата тангенса угла $\alpha$ и 1, равна обратному квадрату косинуса этого угла. Данное тождество справедливо для всех $\alpha$, отличных от $\displaystyle \frac{\pi}{2}+ \pi z$.

$\displaystyle 1+ctg^{2} \alpha=\frac{1}{\sin^{2}\alpha}$ — сумма 1 и квадрат котангенса угла $\alpha$, равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого $\alpha$, отличного от $\pi z$.

18 февраля 2022 г.

Тема: Периодичность и знаки тригонометрических функций.

Объяснение и обоснование

1. Знаки тригонометрических функций легко определить, исходя из определения этих функций.

  Например,  — это ордината соответствующей точки  единичной окружности. Поэтому значение   будет положительным, если точка имеет положительную ординату, a это будет тогда, когда точка   находится в I или II четверти (рис. 67). . Если точка   находится в III или IV четверти, то ее ордината отрицательна, и поэтому  тоже отрицателен. Аналогично, учитывая, что  — это абсцисса соответствующей точки , получаем, что >0  в I и IV четвертях (абсцисса точки   положительна) и <0  во II и III четвертях (абсцисса точки   отрицательна) (рис. 68).

Поскольку  там, где  и   имеют одинаковые знаки, то есть в I и III четвертях, и  там, где  и  имеют разные знаки, то есть во II и IV четвертях (рис. 69). 

2. Четность и нечетность тригонометрических функций.

 Чтобы исследовать тригонометрические функции на четность и нечетность, заметим, что на единичной окружности точки  и расположены симметрично относительно оси Ox (рис. 70). Следовательно, эти точки имеют одинаковые абсциссы и противоположные ординаты.

Тогда 

Таким образом,  — четная функция, а — нечетная.

Поэтому — нечетные функции. 

Замечание. Приведенное исследование четности и нечетности функций   и   неявно опирается на утверждение, что точки   и будут расположены симметрично относительно оси Ох при любом значении  Приведем план возможного обоснования этого утверждения. 

1)   Если  или  то утверждение очевидно в силу симметрии единичной окружности относительно оси Ох, проходящей через центр окружности.

2)   В силу этой же симметрии утверждение очевидно и при  или

3)   Для всех других значений угла используем утверждение (которое мы примем без доказательства), что его радианную меру α можно записать в виде  (радиан) удовлетворяет неравенству и, учитывая, что на единичной окружности углам и  соответствует одна и та же точка, сводим этот случай к случаю 2.

Четность и нечетность тригонометрических функций можно применять для вычисления значений тригонометрических функций отрицательных  углов (чисел).

Например, 

3. Периодичность тригонометрических функций. Множество процессов и явлений, которые происходят в природе и технике, имеют повторяющийся характер (например, движение Земли вокруг Солнца, движение маховика). Для описания процессов такого рода используют так называемые периодипериодические функции.

Функция y = f (x) называется периодической с периодом T ≠ 0, если для любого x из области определения функции числа (x + T) и (x – T) также f (x + T) = f (x). 

Из приведенного определения получаем, что f (x – T) = f ((x – T) + T) = f (x), то есть, если T — период функции f (x), то и – T тоже период этой функции. Также можно доказать, что ±2Т, ±3Т, ..., ±kТ — тоже периоды этой функции (k ∈ N).

  Учитывая, что на единичной окружности числам (углам)  где  соответствует одна и та же точка (рис. 71), получаем:

Тогда   является периодом функций  и .

При k = 1 получаем, что — это период функций  и .

Докажем, что эти функции не могут иметь меньший положительный период. Чтобы доказать, что  — наименьший положительный период косинуса, допустим, что T > 0 — период функции . Тогда для любого значения x выполняется равенство  cos (x + T) = cos x.  Взяв x = 0, получаем cos T = 1. Но это означает, что на единичной окружности при повороте на угол T точка  снова попадает в точку , то есть , где k ∈ Z. Таким образом, любой период косинуса должен быть кратным, а значит,

 — наименьший положительный период косинуса.

  Чтобы обосновать, что  — наименьший положительный период функции sin x, достаточно в равенстве sin (x + T) = sin x, которое выполняется для любых значений x, взять . Получаем Но это означает, что при повороте на угол  точка  попадает в точку A (0;1) (рис. 71), то есть  таким образом . Следовательно, любой период синуса должен быть кратным , а значит,

 — наименьший положительный период косинуса.

    Если учесть, что на единичной окружности точки   и   являются диаметрально противоположными, то этим точкам соответствует одна и та же точка на линии тангенсов (рис. 72) или на линии котангенсов (рис. 73). Тогда также 

То есть периодом функций tg x и ctg x является (k ≠ 0, k ∈ Z).

 Наименьшим положительным периодом для функций tg x и ctg x является 

Чтобы доказать это, достаточно в равенстве tg (x + T) = tg x взять x = 0. 

Тогда получим tg T = 0. Таким образом, T =, где k ∈ Z. Итак, любой период тангенса должен быть кратным  а значит,  -  наименьший положительный период тангенса. Аналогично в соответствующем равенстве для ctg x достаточно взять . 

 Чтобы иметь представление о поведении графика периодической функции y = f (x), напомним, что по определению график функции y = f (x) состоит из всех точек M координатной плоскости, которые имеют координаты (x; y) = (x; f (x)). Первая координата для точек графика выбирается произвольно из области определения функции. Выберем как первую координату значение x + T (или в обобщенном виде — значение x + kT при целом значении k) и учтем, что для периодической функции f(x + T) = f(x – T) = f (x) (в общем случае f (x + kT) = f (x)). Тогда графи-

ку функции y = f (x) будет принадлежать также точка M1 координатной плоскости с координатами: (x + T; y) = (x + T; f (x + T)) = (x + T; f (x)).

Точку M1 (x + T; f (x)) можно получить из точки M (x; f (x)) параллельным переносом вдоль оси Ox на T единиц (рис. 74). В общем случае точку M2 (x + kT; f (x)) можно получить из точки M (x; f (x)) параллельным переносом вдоль оси Ox на kT единиц. Таким образом, через промежуток  T вид графика периодической функции будет повторяться. Поэтому для построения графика периодической функции с периодом T достаточно построить график на любом промежутке длиной T(например, на проме-жутке [0;T]), а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние kT, где k — любое натуральное число.