2 февраля 2022 г.
Тема: Цилиндр и конус. Осевые сечения и сечения параллельные основанию. Решение задач.
Цилиндр
Усеченный конус
26 января 2022 г.
Тема: Тела вращения. Цилиндр и конус.
Цилиндр
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. Пусть h — высота цилиндра, r — радиус цилиндра, Sбок — площадь боковой поверхности цилиндра, Sполн — площадь полной поверхности цилиндра, V — объем цилиндра. Тогда имеют место следующие соотношения: |
|
![]()
![]()
![]()
Конус
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. Пусть h — высота конуса, r — радиус основания конуса, l — образующая конуса, Sбок — площадь боковой поверхности конуса, Sполн — площадь полной поверхности конуса, V — объем конуса. Тогда имеют место следующие соотношения: |
|
![]()
![]()
![]()
Сечение конуса плоскостью, параллельной основанию
Сечение конуса плоскостью, параллельной его основанию (перпендикулярной высоте), делит высоту и образующие конуса на пропорциональные отрезки.
Площади сечений конуса, параллельных его основанию, относятся как квадраты их расстояний от вершины конуса.
Усеченный конус
Пусть h — высота усеченного конуса, r и r1 — радиусы основания усеченного конуса, l — образующая усеченного конуса, Sбок — площадь боковой поверхности усеченного конуса, V — объем усеченного конуса. Тогда имеют место следующие соотношения: |
|
![]()
26 января 2022 г.
КОНТРОЛЬНАЯ РАБОТА.
1. 1. Найти
площадь полной поверхности пря мой призмы в основании которой лежит: равнобедренная
трапеция с основаниями 1см и 7см и боковой стороной 5см, если боковое ребро
призмы равно 4см.
2. Найдите высоту пирамиды в основании которой лежит равнобедренный треугольник с основанием: 6см и высотой 9см, если каждое боковое ребро пирамиды равно 13см.
3. Основание прямой призмы — прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань — квадрат.
1. 4...Ребро
правильного тетраэдра DABC равно а. Постройте сечение тетраэдра,
проходящее через середину ребра DA параллельно плоскости DBC, и найдите площадь
этого сечения.
19 января 2022 г.
Тема: Многогранники.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
А)
Б)

Рисунок 1 – разные подходы к определению многоугольника
По аналогии с первым толкованием понятия многоугольника рассматривается следующее толкование понятия многогранника. Многогранник - поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. В данной трактовке многогранник можно называть еще многогранной поверхностью.
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
Примеры многогранников
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)

Рисунок 2 – изображение октаэдра
Элементы многогранника
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Виды многогранников
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).

Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Утверждение. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600.
Пояснить данное утверждение поможет рисунок 4. “Разрежем” многогранник вдоль его ребер и все его грани с общей вершиной расположим так, чтобы они оказались в одной плоскости. Видим, что сумма всех плоских углов действительно меньше 3600.

Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
12 января 2022 г.
Тема: Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр)
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.
Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n ≥ 6.
Сумма всех плоских углов при каждой вершине выпуклого правильного многогранника меньше 3600.
Существует всего пять видов правильных многогранников:
1. Правильный тетраэдр – составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 1800.
2. Правильный октаэдр – составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 2400.
3. Правильный икосаэдр – составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 3000.
4. Правильный гексаэдр (куб) – составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 2700.
5. Правильный додекаэдр – составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 3240.

Практическая часть:
Задача № 1
Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Решение

Пусть a – ребро куба, A1B и A1C1 – диагонали. Значит ∠ BA1C1 – искомый.
1) Так как все грани куба – равные квадраты, то диагонали граней равны, то есть A1B=A1C=BC1=![]() .
.
2) ΔA1BC1 – равносторонний, значит ∠ BA1C1=600.
Ответ: 600
Тема: Сечения многогранников, построение сечений.
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Определение: две прямые параллельны, если они лежат в одной плоскости и не пересекаются. Если через две прямые нельзя провести одну плоскость, то такие прямые скрещиваются.
Теорема о параллельности трех прямых: если a∥b, b∥c, то и a∥c. Определение: прямая и плоскость параллельны, если они не имеют общих точек. Признак параллельности прямой и плоскости: прямая, не лежащая в плоскости, параллельна этой плоскости, если она параллельна некоторой прямой из этой плоскости.
Определение: две плоскости параллельны, если они не имеют общих точек.
Признак параллельности двух плоскостей: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости параллельны.
Если две плоскости пересекаются, то их линия пересечения — прямая.
Если две параллельные плоскости пересечены третьей, то их линии пересечения параллельны (см. рис.)
Если плоскости α и β пересекаются по прямой a, а плоскости β и γ пересекаются по прямой b, причем a∥b, то плоскости α и γ пересекутся по прямой c∥a∥b.
Следом называется прямая, по которой плоскость сечения пересекает плоскость любой из граней многогранника.
Примеры и разбор решения заданий тренировочного модуля
№1 SABCD – четырехугольная пирамида, в основании которой лежит квадрат ABCD, а две боковые грани SAB и SAD представляют собой прямоугольные треугольники с прямым углом ∠A. Найдите площадь сечения пирамиды плоскостью α, если SA=AB=a.

Решение:
сначала построим сечение по условию задачи.
1)Пусть AC∩BD=O. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Заметим, что т.к. ∠SAB=∠SAD=90∘⇒SA⊥(ABC). Проведем в плоскости SAC прямую OK∥SC. Т.к. O – середина AC, то по теореме Фалеса K – середина SA. Через точку K в плоскости SAB проведем KM∥SB (следовательно, M – середина AB). Таким образом, плоскость, проходящая через прямые OK и KM, и будет искомой плоскостью. Необходимо найти сечение пирамиды этой плоскостью. Соединив точки O и M, получим прямую MN. Т.к. α∥(SBC),то α пересечет плоскость SCD по прямой NP∥SC (если NP∩SC≠∅, то α∩(SBC)≠∅, что невозможно ввиду их параллельности). Таким образом, KMNP – искомое сечение, причем KP∥AD∥MN⇒ это трапеция.
 2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3
2)Т.к. все точки K,M,N,P – середины отрезков SA,AB,CD,SD соответственно, то: а) MN=AD=a б) KP=1/2AD=a/2 в) KM=1/2SB=a 2/2 Заметим, что по теореме о трех перпендикулярах SB⊥BC⇒KM⊥MN. Таким образом, KMNP – прямоугольная трапеция. SKMNP=(KP+MN)* KM/ 2 =3 a2/8
a2/8
Ответ:3 a2/8
a2/8
№2 Найди площадь сечения прямой призмы, проходящей через середины ребер, если  =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .
=120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см2 .

Решение:
боковая грань прямой призмы является прямоугольником.
Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.



То есть большая боковая грань содержит большую сторону основания.
По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.
=120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.


Получим, что длина стороны АС=7см.
Зная большую сторону основания и площадь наибольшей боковой грани призмы, длину высоты призмы вычислить нетрудно.
Получим, что длина высоты призмы равна  .
.
Найдем площадь основания, а оно равно площади сечения, по формуле  .
.
Мы воспользуемся второй формулой. Получим, что площадь основания равна  .
.
Ответ: 15 /4 см2
/4 см2
№3 На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:QB=1:2. Точка P — середина ребра AS.
Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.

Решение:
пусть сторона основания пирамиды равна 3а, а высота пирамиды равна h. Тогда площадь сечения DSB равна

 S=BD*SO/2= 3 =6
S=BD*SO/2= 3 =6
откуда ah=2 .
Площадь сечения DPQ равна

Ответ: 
№4
Дана правильная треугольная пирамида SABC с вершиной S. Через середину ребра AC и точки пересечения медиан граней ASB и CSB проведена плоскость. Найдите площадь сечения пирамиды этой плоскостью, если AB=21,AS=12 .
.

Решение:
пусть LK∩SO=H. Тогда по теореме о трех перпендикулярах HK⊥AC как наклонная (HO⊥(ABC),OK⊥AC как проекция). Следовательно, и LK⊥AC.


 Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12
Тогда SALC=AC⋅LK/2 Рассмотрим △SKB: BK=AB⋅ /2=21 /2⇒cosB=7 /12 .
.
Тогда по теореме косинусов для △KLB: KL2=729/4⇒KL=27/2
Значит, SALC=567/4=141,75
Ответ : 141,75
№5
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK : KA1 = 1 : 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M, АВ=4, АА1=6. Найдите площадь сечения.

Решение:
По теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно  перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы,
перпендикулярны, равна половине произведения диагоналей. Найдем их: KL=AC=4 как диагональ квадрата, лежащего в основании призмы,  тогда
тогда
по теореме Пифагора.

Тогда
Ответ: 8
16 декабря 2021 г.
Тема: Треугольная пирамида.
Решение задач.
- правильная пирамида (вершина проецируется в центр основания);
- пирамида, вершина которой проецируется в центр описанной окружности;
- пирамида, вершина которой проецируется в центр вписанной окружности;
- пирамида, высота которой совпадает с боковым ребром;
- пирамида, высота которой также является высотой боковой грани.
15 декабря 2021 г.
Тема: Правильная пирамида, ее поверхность.
Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой.



13 декабря 2021 г.
Тема: Пирамида, ее основание, боковые ребра, высота, боковая
поверхность.
Пирамида –
многогранник, основание которого — многоугольник , а остальные
грани — треугольники, имеющие общую вершину.
По
числу углов основания различают
пирамиды треугольные, четырёхугольные и т. д.
Вершина
пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости
основания.
Основание —
многоугольник, которому не принадлежит вершина пирамиды.
Апофема —
высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота —
отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её
основания (концами этого отрезка являются вершина пирамиды и основание
перпендикуляра).
Диагональное
сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ
основания.
Некоторые
свойства пирамиды
1) Если
все боковые ребра равны, то
– около
основания пирамиды можно описать окружность, причём вершина пирамиды
проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если
боковые ребра образуют с плоскостью основания равные углы, то все боковые
ребра пирамиды равны.
Если
около основания пирамиды можно описать окружность, причём вершина пирамиды
проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно
и обратное.
10 декабря 2021 г.
Тема: Призма. Решение задач.
Задача № 1. Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10 дм. Найдите площадь боковой и полной поверхности призмы.
Решение:
Используя свойство – диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, найдем сторону .
OD=0,8 дм, OC=1,5
дм
Рассмотрим ∆СОD-
прямоугольный.
AB=BC=CD=AD=1,7 дм
S=4∙ (1,7∙10)=68 дм2.
Ответ: 68 дм2
Задача №
2. Ребро
куба равно а. заполните таблицу, используя формулы:
Диагональ грани:d=
a√2
Диагональ куба: D=
a√3
Периметр
основания: P= 4a
Площадь грани: S=a2
Площадь диагонального сечения: Q= a2√2
Площадь
поверхности куба: S= 6a2
Периметр и площадь
сечения, проходящего через концы трех ребер, выходящих из одной вершины: P=
3a√2 ,
Задача №
3. Сторона
основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см.
Найдите Sсеч, проходящего через сторону верхнего основания и противолежащую
вершину нижнего основания.
Решение:
Треугольник A1B 1C1 - равнобедренный(A1 B=C1B как диагональ равных
граней)
1)Рассмотрим
треугольник BCC1– прямоугольный
BC1 2 =BС2 +CC1 2
BC1= ![]() =10 см
=10 см
2) Рассмотрим
треугольник BMC1– прямоугольный
BC1 2 = BM2 + M C1 2
BM2 = BC1 2 -M C1 2
BM2 =100-16=84
3) Sсеч = ![]() A1C1 *BM=
A1C1 *BM= ![]() ∙8∙2
∙8∙2 ![]() =8
=8 ![]() см2
см2
Тема: Правильная призма. Параллелепипед. Куб.
Тема: Правильная призма. Параллелепипед. Куб.
Призма
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:

где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
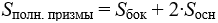
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).
- Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.
Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы - прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):


где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
- Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Параллелепипед
Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.

Другие свойства и определения:
- Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
- Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
- Параллелепипед имеет шесть граней и все они – параллелограммы.
- Противоположные грани параллелепипеда попарно равны и параллельны.
- У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
- Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
- Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
- Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = Sосн∙h).
- Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:
d2 = a2 + b2 + c2.
- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:


- Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.
- Диагональ куба d и длина его ребра a связаны соотношением:

- Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу дляобъема куба:
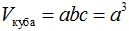

08 декабря 2021 г.
Тема: Прямая и наклонная
призма, ее основание, боковые ребра, высота, боковая поверхность.
Призма – это объемное тело, которое
имеет большое количество граней.
Данная фигура имеет в основаниях два многоугольника, которые расположены в параллельных плоскостях, а все боковые грани имеют форму параллелограмма.
Рис 1.
Рис. 2
Итак, давайте разберемся, из чего состоит призма. Для этого обратите внимание на Рис.1
Как уже говорилось ранее, у призмы есть два основания, которые параллельны друг другу – это пятиугольники ABCEF и GMNJK. Более того, данные многоугольники равны между собой.
Все остальные грани призмы называются боковыми гранями – они состоят из параллелограммов. Например, BMNC, AGKF, FKJE и т.д.
Общая поверхность всех боковых граней называется боковой поверхностью.
Каждая пара соседних граней имеет общую сторону. Такая общая сторона называется ребром. Например МВ, СЕ, АВ и т.д.
Если верхнее и нижнее основание призмы соединить перпендикуляром, то он будет называться высотой призмы. На рисунке высота отмечена, как прямая ОО1.
Существует две основных разновидности призмы: наклонная и прямая.
Если боковые ребра призмы не являются перпендикулярными к основаниям, то такая призма называется наклонной.
Если все ребра призмы перпендикулярны к основаниям, то такая призма называется прямой.
Если в основаниях призмы лежат правильные многоугольники (те, у которых стороны равны), то такая призма называется правильной.
Если основания у призмы не параллельны друг другу, то такая призма будет называться усеченной.
Её Вы можете наблюдать на Рис.2
Формулы для нахождения объема, площади призмы
Существует три основных формулы нахождения объема. Отличаются они друг от друга применением:
Аналогичные формулы для нахождения площади поверхности призмы:
06 декабря 2021 г.
Тема: Выпуклые многогранники.
Теорема Эйлера.
Многогранник называется выпуклым, если он является
выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и
соединяющий их отрезок.
На рисунке 1 приведены примеры выпуклых и невыпуклых многогранников.
Рассмотрим некоторые свойства выпуклых многогранников.
Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Доказательство. Пусть F - какая-нибудь грань многогранника M,
и A, B – точки, принадлежащие грани F (рис.
2). Из условия выпуклости многогранника M, следует, что
отрезок AB целиком содержится в многограннике M.
Поскольку этот отрезок лежит в плоскости многоугольника F, он
будет целиком содержаться и в этом многоугольнике, т.е. F -
выпуклый многоугольник.
Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей
вершиной, основания которых образуют поверхность многогранника.
Доказательство. Пусть M - выпуклый многогранник. Возьмем какую-нибудь
внутреннюю точку S многогранника M, т.е. такую его
точку, которая не принадлежит ни одной грани многогранника M.
Соединим точку S с вершинами многогранника M отрезками
(рис. 3). Заметим, что в силу выпуклости многогранника M, все эти
отрезки содержатся в M. Рассмотрим пирамиды с вершиной S,
основаниями которых являются грани многогранника M. Эти пирамиды
целиком содержатся в M, и все вместе составляют многогранник M.
Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей
грани.
Доказательство. Предположим противное, т.е. существуют точки A и B многогранника M,
лежащие по разные стороны от плоскости некоторой его грани N (рис.
4). Рассмотрим пирамиды с вершинами в точках A, B,
основаниями которых является грань N. В силу выпуклости
многогранника, эти пирамиды целиком в нем содержатся. Это противоречит тому,
что N является гранью многогранника M.
Для выпуклых многогранников имеет место свойство, связывающее число его
вершин, ребер и граней, доказанное в 1752 году Леонардом Эйлером, и получившее
название теоремы Эйлера.
Прежде чем его сформулировать рассмотрим известные нам многогранники и
заполним следующую таблицу, в которой В - число вершин, Р - ребер и Г - граней
данного многогранника:
|
Название многогранника |
В |
Р |
Г |
|
Треугольная пирамида |
|
|
|
|
Четырехугольная пирамида |
|
|
|
|
Треугольная призма |
|
|
|
|
Четырехугольная призма |
|
|
|
|
n-угольная пирамида |
n+1 |
2n |
n+1 |
|
n-угольная призма |
2n |
3n |
n+2 |
|
n-угольная усеченная пирамида |
2n |
3n |
n+2 |
Из этой таблицы непосредственно видно, что для всех выбранных многогранников
имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо
не только для этих многогранников, но и для произвольного выпуклого
многогранника.
Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство
В - Р + Г = 2,
где В - число вершин, Р - число ребер и Г - число граней данного многогранника.
Доказательство. Для доказательства этого равенства представим
поверхность данного многогранника сделанной из эластичного материала. Удалим
(вырежем) одну из его граней и оставшуюся поверхность растянем на плоскости.
Получим многоугольник (образованный ребрами удаленной грани многогранника),
разбитый на более мелкие многоугольники (образованные остальными гранями
многогранника).
Заметим, что многоугольники можно деформировать, увеличивать, уменьшать или
даже искривлять их стороны, лишь бы при этом не происходило разрывов сторон.
Число вершин, ребер и граней при этом не изменится.
Докажем, что для полученного разбиения многоугольника на более мелкие
многоугольники имеет место равенство
(*) В - Р + Г ' = 1,
где В – общее число вершин, Р – общее число ребер и Г ' – число
многоугольников, входящих в разбиение. Ясно, что Г '= Г – 1, где Г – число
граней данного многогранника.
Докажем, что равенство (*) не изменится, если в каком-нибудь многоугольнике
данного разбиения провести диагональ (рис. 5, а). Действительно,после
проведения такой диагонали в новом разбиении будет В вершин, Р+1 ребер и
количество многоугольников увеличится на единицу. Следовательно, имеем
В - (Р + 1) + (Г '+1) = В – Р + Г '.
Пользуясь этим свойством, проведем диагонали, разбивающие входящие
многоугольники на треугольники, и для полученного разбиения покажем
выполнимость равенства (*) (рис. 5, б). Для этого будем последовательно
убирать внешние ребра, уменьшая количество треугольников.
При этом возможны два случая:
а) для удаления треугольника ABC требуется снять два
ребра, в нашем случае AB и BC;
б) для удаления треугольника MKN требуется снять одно
ребро, в нашем случае MN.
В обоих случаях равенство (*) не изменится. Например, в первом случае после
удаления треугольника граф будет состоять из В – 1 вершин, Р – 2 ребер и Г ' –
1 многоугольника:
(В - 1) - (Р + 2) + (Г ' – 1) = В – Р + Г '.
Самостоятельно рассмотрите второй случай.
Таким образом, удаление одного треугольника не меняет равенство (*).
Продолжая этот процесс удаления треугольников, в конце концов, мы придем к
разбиению, состоящему из одного треугольника. Для такого разбиения В = 3, Р =
3, Г ' = 1 и, следовательно, B – Р + Г ' = 1. Значит, равенство (*) имеет место
и для исходного разбиения, откуда окончательно получаем, что для данного
разбиения многоугольника справедливо равенство (*). Таким образом, для
исходного выпуклого многогранника справедливо равенство В - Р + Г = 2.
Пример многогранника, для которого не выполняется соотношение Эйлера,
показан на рисунке 6. Этот многогранник имеет 16 вершин, 32 ребра и 16 граней.
Таким образом, для этого многогранника выполняется равенство В – Р + Г = 0.
Используя соотношение Эйлера, докажем, следующее свойство выпуклых
многогранников.
Свойство 4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или
равным пяти.
Действительно, в каждой вершине многогранника сходится, по крайней мере,
три ребра. Если количество вершин равно В и в каждой из них сходится три ребра,
то общее число ребер будет больше или равно 3В : 2. Делить на два нужно потому,
что при таком подсчете ребер мы каждое ребро посчитаем дважды – один раз, как
ребро выходящее из одной его вершины, а второй раз, как ребро, выходящее из
второй его вершины. Таким образом, для любого многогранника имеет место
неравенство 3В ![]() 2Р.
2Р.
Обозначим через Гn число граней с n ребрами.
Тогда Г = Г3 + Г4 + Г5 + Г6.
Каждая треугольная грань имеет три ребра и число треугольных граней равно Г3.
Поэтому общее число ребер в треугольных гранях равно 3Г3.
Аналогично, общее число ребер в четырехугольных гранях равно 4Г4 и
т. д.
Поскольку каждое ребро многогранника содержится ровно в двух гранях, то при
таком подсчете ребер, мы каждое ребро посчитаем дважды и, следовательно, будет
иметь место равенство 2Р = 3Г3 + 4Г4 + 5Г5 +
6Г6.
Воспользуемся равенством 6В – 6Р + 6Г = 12, получающимся умножением обеих
частей сооотношения Эйлера на 6. По доказанному выше, имеет место неравенство
6В ![]() 4Р и, следовательно,
неравенство 6Г – 2Р
4Р и, следовательно,
неравенство 6Г – 2Р ![]() 12. С другой стороны, 6Г = 6Г3 +
6Г4 + 6Г5 + 6Г6, 2Р = 3Г3 +
4Г4 + 5Г5 + 6Г6. Подставляя эти
выражения в неравенство, получим неравенство 3Г3 + 2Г4 +
Г5 + 0Г6 – Г7 –
12. С другой стороны, 6Г = 6Г3 +
6Г4 + 6Г5 + 6Г6, 2Р = 3Г3 +
4Г4 + 5Г5 + 6Г6. Подставляя эти
выражения в неравенство, получим неравенство 3Г3 + 2Г4 +
Г5 + 0Г6 – Г7 – ![]() 12. В левой части, начиная с
Г7 стоят отрицательные числа. Поэтому для того, чтобы вся сумма
была больше или равна 12 нужно, чтобы хотя бы одно из чисел Г3 или
Г4 или Г5 было отлично от нуля, т.е. в
многограннике существовала грань с соответствующим числом ребер.
12. В левой части, начиная с
Г7 стоят отрицательные числа. Поэтому для того, чтобы вся сумма
была больше или равна 12 нужно, чтобы хотя бы одно из чисел Г3 или
Г4 или Г5 было отлично от нуля, т.е. в
многограннике существовала грань с соответствующим числом ребер.
03 декабря 2021 г.
Тема: Вершины, ребра, грани многогранника. Развертка.
Многогранник – геометрическое тело,
ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие
многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника
(вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две
вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по
одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого
найдется по крайней мере одна грань такая, что плоскость, проведенная через эту
грань, делит данный многогранник на две или более частей.
К определению понятия многогранника существует
два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в
планиметрии под многоугольником мы понимали замкнутую линию без
самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно
рассматривать как часть плоскости, ограниченную этой линией, включая ее саму
(рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым
толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть
плоская поверхность.
А)
Б)
Рисунок 1 – разные подходы к определению
многоугольника
По аналогии с первым толкованием понятия
многоугольника рассматривается следующее толкование понятия многогранника.
Многогранник - поверхность, составленная из многоугольников и ограничивающая
некоторое геометрическое тело. В данной трактовке многогранник можно называть
еще многогранной поверхностью.
Вторая трактовка понятия определяет
многогранник как геометрическое тело, ограниченное конечным числом плоских
многоугольников.
В дальнейшем, мы будем использовать
вторую трактовку понятия многогранника.
Примеры многогранников
Уже известные вам тетраэдр и
параллелепипед являются многогранниками. Потому что они являются
геометрическими телами, ограниченные конечным числом плоских многоугольников.
Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Элементы многогранника
Многоугольники, ограничивающие
многогранник, называются его гранями. Так, у тетраэдра и
октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его
название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от
греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами,
а концы ребер — вершинами многогранника. Отрезок, соединяющий две
вершины, не принадлежащие одной грани, называется диагональю многогранника.
Виды многогранников
Многогранник называется выпуклым,
если он расположен по одну сторону от плоскости каждой его грани. В остальных
случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
02 декабря 2021 г.
КОНТРОЛЬНАЯ РАБОТА
01 декабря 2021 г.
Тема: Решение неравенств и их
систем. Решение уравнений и неравенств. Практическое
занятие №12.
Решение
дробно-рационального неравенства
Пример. Решить неравенство:
Решение
Решаем соответствующее уравнение:![]()
Разложим числитель первой дроби и знаменатель второй дроби на множители:
Домножим числитель и знаменатель первой дроби на ![]() , приведя, таким образом, дроби к
общему знаменателю:
, приведя, таким образом, дроби к
общему знаменателю:
Домножим обе части уравнения на
В полученном уравнении вынесем ![]() за скобку:
за скобку:
Раскроем квадрат:
Приведем подобные слагаемые:
Откуда:
Решим второе уравнение. По теореме Виета:
Расставляем на оси особые точки ОДЗ и корни уравнения. Методом пробной
точки определяем знаки на каждом интервале. Выбираем интервалы с нужным знаком
(см. рис. 3).
Рис. 3. Иллюстрация к примеру
Получаем ответ:
Ответ:
.
В конце нашего занятия мы разберем решение иррационального неравенства.
Задание 8. Решить неравенство:
Решение
Сначала укажемОДЗ. Подкоренные выражения должны быть неотрицательны. При
этом не должно быть деления на ноль, то есть:
Далее нужно решить само неравенство. Это можно сделать сразу методом
интервалов, но этот путь будет достаточно громоздким. Попробуем его немного
упростить.
1. Умножим обе части неравенства на положительную величину ![]() :
:
2. Слева и справа стоят неотрицательные величины. При возведении в квадрат
обеих частей знак неравенства сохранится. Это верно, поскольку при
положительных значениях аргумента функция  является возрастающей (см.
рис. 4).
является возрастающей (см.
рис. 4).
Рис. 4. При положительных значениях аргумента функция![]() возрастает
возрастает
Большему значению аргумента соответствует большее значение функции:
Таким образом, избавляемся от корней в обеих частях неравенства:
Итак, должно выполняться это неравенство и все неравенства из ОДЗ. То есть
исходное иррациональное неравенство эквивалентно следующей системе неравенств:
Теперь осталось решить каждое из неравенств методом интервалов и найти пересечение полученных областей. Но есть одна маленькая деталь: решить уравнение
будет проблематично, т. к. оно не имеет целых корней. А мы научились решать кубические уравнения только с целыми корнями. Как же быть?Внимательно посмотрим на условия из нашей системы.
, а
. Значит, их произведение
. При этом выражение
, а значит, и больше нуля. То есть из первого второго и четвертого неравенств автоматически следует, что выполняется третье неравенство. Значит, условие
избыточно и нам достаточно решить систему из трех неравенств:
Проще всего решить второе и третье неравенства:
Для решения первого неравенства воспользуемся методом интервалов:
Решаем соответствующее уравнение:
Вынесем х за скобку:
Решая квадратное уравнение, получаем:
Расставляем корни на оси, методом пробной точки определяем знаки на
интервалах, выбираем нужные интервалы (см. рис. 5).
Рис. 5. Иллюстрация к заданию 8
Отметим на оси решения других двух неравенств и найдем их пересечение (см.
рис. 6).
Рис. 6. Иллюстрация к заданию 8
Получаем ответ:
Ответ:
.Итак, мы вспомнили основные методы решения уравнений, неравенств, а также их систем.
26 ноября 2021 г.
Тема: Использование свойств и
графиков функции при решении уравнений и неравенств.
Для решения
неравенств можно пользоваться аналитическим и графическим способами. Но,
несмотря на способ, который Вы выберете, необходимо учитывать свойства функций
и вид их графиков.
Свойства
функций
1. Парность/
непарность
Если функция
на графике является симметричной относительно оси ОУ, то данная функция будет
называться парной. Для такой функции значение функции будет одинаковым, как для
положительных "х", так и для отрицательных.
f(-x) = f(x).
Парной
функцией можно
назвать квадратичную функцию, графиком которой является парабола с вершиной в
начале координат. Так же график выражения в модуле будет являться парной
функцией. Среди тригонометрических функций существует единственная функция,
которую можно назвать парной - косинус без сдвига фаз.
Если функция
симметрична относительно начала координат, то её называют непарной.
f(-x) = -
f(x).
К таким
функциям можно отнести любую функцию, старший член которой будет иметь нечетную
степень или же, например, функция синуса.
Множество
остальных функций нельзя отнести ни к парным, ни к непарным.
2.
Периодичность
Если некоторая функция повторяется через некоторый период. Такие функцию
будут повторяться до бесконечности. К периодичным
функциям относятся все тригонометрические функции, не ограниченные на
некотором промежутке.
3. Нули
функции и промежутки знакопостоянства
Нуль функций - это такое значение ординаты,
при которой функция обращается в нуль.
Когда мы
находим решение уравнений, мы, как раз, находим нули функций. Иными словами
нулем называется точка, в которой график функции пересекает ось ОХ.
Промежутки
знакопостоянства - это
диапазон, в котором функция имеет одинаковый знак, то есть принимает только
положительные, или только отрицательные значения.
Нули функции
разбивает всю числовую прямую на интервалы. Именно относительно нулей
происходит решение неравенств высоких степеней. Чередование знаков на
промежутках происходит именно относительно нулей функции.
Судя по
указанному графику, если нам необходимо найти решение неравенств, где функция
будет больше нуля, нам подходят диапазоны (-10; -8), (-4; 5).
4. Убывание/
возрастание функции
Если на
некотором промежутке [а,б] функция f(x1) < f(x2) для любых x1 < x2, то такую функцию называют монотонно
возрастающей.
Если на
некотором промежутке [а,б] функция f(x1) > f(x2) для любых x1 < x2, то такую функцию называют монотонно
убывающей.
5. Минимум/
максимум/ экстремум
Если для
некоторого участка функции в точке выполняется неравенство f(x1) < f(x0)(f(x1) > f(x0)), то точка x0 является максимумом
(минимумом) функции.
То есть
точкой, в которой функция будет принимать максимальное (минимальное) значение.
Точки, в
которых функция принимает максимальное или минимальное значения, называются экстремумами
функции.
В данном
случае xmax, xmin - точки экстремума, а функция в данной точке называется
экстремумом функции.
Точки, в
которых производная функции равная нулю или не существует вовсе, называются критическими
точками.
Если
производная некоторой функции в точке равна нулю, а вторая производная отлична
от нуля, то данная точка будет точкой максимума, если вторая производная меньше
нуля, и минимума, если она больше нуля.
Тема: Правильная призма. Параллелепипед. Куб.
Тема: Использование свойств и графиков функции при решении уравнений и неравенств.
Для решения
неравенств можно пользоваться аналитическим и графическим способами. Но,
несмотря на способ, который Вы выберете, необходимо учитывать свойства функций
и вид их графиков.
Свойства функций
1. Парность/ непарность
Если функция
на графике является симметричной относительно оси ОУ, то данная функция будет
называться парной. Для такой функции значение функции будет одинаковым, как для
положительных "х", так и для отрицательных.
f(-x) = f(x).
Парной
функцией можно
назвать квадратичную функцию, графиком которой является парабола с вершиной в
начале координат. Так же график выражения в модуле будет являться парной
функцией. Среди тригонометрических функций существует единственная функция,
которую можно назвать парной - косинус без сдвига фаз.
Если функция симметрична относительно начала координат, то её называют непарной.
f(-x) = -
f(x).
К таким функциям можно отнести любую функцию, старший член которой будет иметь нечетную степень или же, например, функция синуса.
Множество остальных функций нельзя отнести ни к парным, ни к непарным.
2. Периодичность
Если некоторая функция повторяется через некоторый период. Такие функцию будут повторяться до бесконечности. К периодичным функциям относятся все тригонометрические функции, не ограниченные на некотором промежутке.
3. Нули функции и промежутки знакопостоянства
Нуль функций - это такое значение ординаты, при которой функция обращается в нуль.
Когда мы
находим решение уравнений, мы, как раз, находим нули функций. Иными словами
нулем называется точка, в которой график функции пересекает ось ОХ.
Промежутки знакопостоянства - это диапазон, в котором функция имеет одинаковый знак, то есть принимает только положительные, или только отрицательные значения.
Нули функции разбивает всю числовую прямую на интервалы. Именно относительно нулей происходит решение неравенств высоких степеней. Чередование знаков на промежутках происходит именно относительно нулей функции.
Судя по указанному графику, если нам необходимо найти решение неравенств, где функция будет больше нуля, нам подходят диапазоны (-10; -8), (-4; 5).
4. Убывание/ возрастание функции
Если на некотором промежутке [а,б] функция f(x1) < f(x2) для любых x1 < x2, то такую функцию называют монотонно возрастающей.
Если на некотором промежутке [а,б] функция f(x1) > f(x2) для любых x1 < x2, то такую функцию называют монотонно убывающей.
5. Минимум/ максимум/ экстремум
Если для некоторого участка функции в точке выполняется неравенство f(x1) < f(x0)(f(x1) > f(x0)), то точка x0 является максимумом (минимумом) функции.
То есть
точкой, в которой функция будет принимать максимальное (минимальное) значение.
Точки, в которых функция принимает максимальное или минимальное значения, называются экстремумами функции.
В данном
случае xmax, xmin - точки экстремума, а функция в данной точке называется
экстремумом функции.
Точки, в которых производная функции равная нулю или не существует вовсе, называются критическими точками.
Если производная некоторой функции в точке равна нулю, а вторая производная отлична от нуля, то данная точка будет точкой максимума, если вторая производная меньше нуля, и минимума, если она больше нуля.
Тема: Правильная призма. Параллелепипед. Куб.
Призма
Определения:
- Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
- Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.
- Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.
- Боковая поверхность – объединение боковых граней.
- Полная поверхность – объединение оснований и боковой поверхности.
- Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.
- Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.
- Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.
- Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.
- Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.
- Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства и формулы для призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
- Объём призмы равен произведению её высоты на площадь основания:

где: Sосн – площадь основания (на чертеже это, например, ABCDE), h – высота (на чертеже это MN).
- Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания:
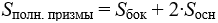
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы (на чертеже ниже перпендикулярное сечение это A2B2C2D2E2).
- Углы перпендикулярного сечения – это линейные углы двугранных углов при соответствующих боковых рёбрах.
- Перпендикулярное (ортогональное) сечение перпендикулярно ко всем боковым граням.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на длину бокового ребра:

где: Sсеч – площадь перпендикулярного сечения, l – длина бокового ребра (на чертеже ниже это, например, AA1или BB1 и так далее).
- Площадь боковой поверхности произвольной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра:

где: Pсеч – периметр перпендикулярного сечения, l – длина бокового ребра.

Виды призм в стереометрии:
- Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (изображены выше). Основания такой призмы, как обычно, расположены в параллельных плоскостях, боковые рёбра не перпендикулярны этим плоскостям, но параллельны между собой. Боковые грани – параллелограммы.
- Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию. В прямой призме боковые ребра являются высотами. Боковые грани прямой призмы - прямоугольники. А площадь и периметр основания равны соответственно площади и периметру перпендикулярного сечения (у прямой призмы, вообще говоря, перпендикулярное сечение целиком является такой же фигурой, как и основания). Поэтому, площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы):


где: Pосн – периметр основания прямой призмы, l – длина бокового ребра, равная в прямой призме высоте (h). Объем прямой призмы находится по общей формуле: V = Sосн∙h = Sосн∙l.
- Правильная призма – призма в основании которой лежит правильный многоугольник (т.е. такой, у которого все стороны и все углы равны между собой), а боковые ребра перпендикулярны плоскостям основания. Примеры правильных призм:

Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Параллелепипед
Определение: Параллелепипед – это призма, основания которой параллелограммы. В этом определении ключевым словом является «призма». Таким образом, параллелепипед – это частный случай призмы, которая отличается от общего случая только тем, что в основании у нее не произвольный многоугольник, а именно параллелограмм. Поэтому все приведенные выше свойства, формулы и определения касающиеся призмы остаются актуальными и для параллелепипеда. Однако, можно выделить несколько дополнительных свойств характерных для параллелепипеда.

Другие свойства и определения:
- Две грани параллелепипеда, не имеющие общего ребра, называются противолежащими, а имеющие общее ребро – смежными.
- Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими.
- Отрезок, соединяющий противолежащие вершины, называется диагональю параллелепипеда.
- Параллелепипед имеет шесть граней и все они – параллелограммы.
- Противоположные грани параллелепипеда попарно равны и параллельны.
- У параллелепипеда четыре диагонали; они все пересекаются в одной точке, и каждая из них делится этой точкой пополам.
- Если четыре боковые грани параллелепипеда – прямоугольники (а основания – произвольные параллелограммы), то он называется прямым (в этом случае, как и у прямой призмы, все боковые ребра перпендикулярны основаниям). Все свойства и формулы для прямой призмы актуальны для прямого параллелепипеда.
- Параллелепипед называется наклонным, если не все его боковые грани являются прямоугольниками.
- Объем прямого или наклонного параллелепипеда рассчитывается по общей формуле для объема призмы, т.е. равен произведению площади основания параллелепипеда на его высоту (V = Sосн∙h).
- Прямой параллелепипед, у которого все шесть граней – прямоугольники (т.е. кроме боковых граней еще и основания являются прямоугольниками), называется прямоугольным. Для прямоугольного параллелепипеда актуальны все свойства прямого параллелепипеда, а также:
- Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением:
d2 = a2 + b2 + c2.
- Из общей формулы для объема призмы можно получить следующую формулу для объема прямоугольного параллелепипеда:


- Прямоугольный параллелепипед, все грани которого являются равными квадратами, называется кубом. Помимо прочего, куб является правильной четырехугольной призмой, и вообще правильным многогранником. Для куба справедливы все свойства прямоугольного параллелепипеда и свойства правильных призм, а также:
- Абсолютно все рёбра куба равны между собой.
- Диагональ куба d и длина его ребра a связаны соотношением:

- Из формулы для объема прямоугольного параллелепипеда можно получить следующую формулу дляобъема куба:
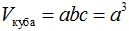

25 ноября 2021 г.
Тема: Равносильность систем.
Решение систем неравенств.
Неравенство —
алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Числовое
неравенство — в записи которого по обе стороны от знака находятся числа
или числовые выражения.
Решение —
значение переменной, при котором неравенство становится верным.
Решить
неравенство значит найти множество, для которых оно выполняется.
Типы
неравенств
Строгие
— используют только больше (>) или меньше (<)
a
< b — это значит, что a меньше, чем b.
a
> b — это значит, что a больше, чем b.
a
> b и b < a означают одно и тоже, то есть равносильны.
Нестрогие
— используют сравнения ≥ (больше или равно) или ≤ (меньше или равно)
a
≤ b — это значит, что a меньше либо равно b.
a
≥ b — это значит, что a больше либо равно b.
знаки
⩽ и ⩾ являются
противоположными.
Другие
типы
a
≠ b — означает, что a не равно b.
a
≫ b — означает, что a
намного больше, чем b.
a
≪ b — означает, что a
намного меньше, чем b.
знаки
>> и << противоположны.
Система
неравенств
Чтобы
щелкать задачки, нам пригодятся свойства числовых неравенств. Вот они:
Если а > b , то b < а. Также наоборот: а < b, то b > а.
Если
а > b и b > c, то а > c. И также если а < b и b < c, то а <
c.
Если
а > b, то а + c > b+ c (и а – c > b – c).
Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям
можно прибавлять или вычитать одну и ту же величину.
Если
а > b и c > d, то а + c > b + d.
Если а < b и c < d, то а + c < b + d.
Два неравенства одинакового смысла можно почленно складывать. Но важно
перепроверять, т.к. возможны исключения. Например, если из 12 > 8 почленно
вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно
вычесть 7 > 2, то полученное будет неверным.
Если
а > b и c < d, то а – c > b – d.
Если а < b и c > d, то а – c < b – d.
Из одного неравенства можно почленно вычесть другое противоположного смысла,
оставляя знак того, из которого вычиталось.
Если
а > b, m — положительное число, то mа > mb и
Обе
части можно умножить или разделить на одно положительное число (знак при этом
остаётся тем же).
Если же а > b, n — отрицательное число, то nа < nb и
Обе
части можно умножить или разделить на одно отрицательное число, при этом знак
поменять на противоположный.
Если
а > b и c > d, где а, b, c, d > 0, то аc > bd.
Если а < b и c < d, где а, b, c, d > 0, то аc < bd.
Неравенства одного смысла на множестве положительных чисел можно почленно
перемножать.
Следствием является: если а > b, где а, b > 0, то а2 > b2, и если
а < b, то а2 < b2. На множестве положительных чисел обе части можно
возвести в квадрат.
Если
а > b, где а, b > 0, то  .
.
Если а < b , то  .
.
Таблица
числовых промежутков
Полезна
тем, что с ее помощью удобно записывать множество решений.
|
Еще
один важный шаг — запись ответа. Вот, как правильно это делать:
Если
знак строгий (>, <), точка на оси будет не закрашена, а скобка — круглой.
Если
знак нестрогий (≥, ≤), точка на оси будет закрашена, а скобка — квадратной.
Скобка,
рядом со знаком бесконечности всегда круглая.
Решение
системы неравенств
Линейное
неравенство — то, в котором неизвестное представлено в первой степени. Для
его решения нужно, чтобы в левой части осталось только неизвестное в первой степени
с коэффициентом равном единице. Алгоритм решения:
1.
Раскрыть скобки, перенести неизвестное в левую часть, числа в правую и привести
подобные слагаемые. Получится одно из следующих видов:
ax
< b,
ax
≤ b,
ax
> b,
ax
≥ b.
2.
Если получилось ax ≤ b.Для его решения необходимо поделить левую и правую часть
на коэффициент перед неизвестным a.
3.
Если a > 0, то x ≤ ba.
Если a < 0, то знак меняется на противоположный.
Получаем x ≥ ba.
4.
Записываем ответ как он есть или в соответствии с таблицей числовых промежутков.
Решим
пример
3
* (2 − x) > 18
|
И
еще один
|
Последний,
чтобы разобраться наверняка
|
19 ноября 2021 г., 24 ноября 2021 г.
Тема: Решение
тригонометрических неравенств.
Неравенства
– это соотношения вида a › b, где a и b – есть выражения, содержащие как
минимум одну переменную. Неравенства могут быть строгими – ‹, › и нестрогими –
≥, ≤.
Тригонометрические
неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a,
F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими
функциями.
Простейшие тригонометрические неравенства
Примером простейшего тригонометрического
неравенства является: sin x ‹ 1/2. Решать подобные задачи принято
графически, для этого разработаны два способа.
Способ 1 – Решение неравенств с помощью
построения графика функции
Чтобы найти промежуток, удовлетворяющий
условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
1.
На
координатной оси построить синусоиду y = sin x.
2.
На
той же оси начертить график числового аргумента неравенства, т. е. прямую,
проходящую через точку ½ ординаты ОY.
3. Отметить точки пересечения двух графиков.
4. Заштриховать отрезок являющийся, решением примера.
Когда в выражении присутствуют строгие
знаки, точки пересечения не являются решениями. Так как наименьший
положительный период синусоиды равен 2π, то запишем ответ следующим образом:
Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки – [ ]. Ответ задачи можно также записать в виде очередного неравенства:
Способ 2 – Решение тригонометрических
неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью
тригонометрического круга. Алгоритм поиска ответов очень прост:
Сначала
стоит начертить единичную окружность.
Затем
нужно отметить значение аркфункции аргумента правой части неравенства на дуге
круга.
Нужно
провести прямую проходящую через значение аркфункции параллельно оси абсциссы
(ОХ).
После
останется только выделить дугу окружности, являющуюся множеством решений
тригонометрического неравенства.
Записать
ответ в требуемой форме.
Разберем
этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки
α и β – значения
Точки
дуги, расположенные выше α и β, являются интервалом решения заданного
неравенства.
Если
нужно решить пример для cos, то дуга ответов будет располагаться симметрично
оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos
можно на схемах приведенных ниже по тексту.
Графические
решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от
косинуса. Это обусловлено свойствами функций.
Арктангенс
и арккотангенс представляют собой касательные к тригонометрической окружности,
а минимальный положительный период для обеих функций равняется π. Чтобы быстро
и правильно пользоваться вторым способом, нужно запомнить на какой из оси
откладываются значения sin, cos, tg и ctg.
Касательная
тангенс проходит параллельно оси OY. Если отложить значение arctg a на
единичном круге, то вторая требуемая точка будет расположено в диагональной
четверти. Углы являются точками разрыва для функции, так как график
стремится к ним, но никогда не достигает.
В случае
с котангенсом касательная проходит параллельно оси OX, а функция прерывается в
точках π и 2π.
Сложные тригонометрические неравенства
Если
аргумент функции неравенства представлен не просто переменной, а целым
выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход
и порядок его решения несколько отличаются от способов описанных выше. Допустим
необходимо найти решение следующего неравенства:
Графическое
решение предусматривает построение обычной синусоиды y = sin x по произвольно
выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек
графика:
В
результате должна получиться красивая кривая.
Для
простоты поиска решения заменим сложный аргумент функции
Пересечение
двух графиков позволяет определить область искомых значений, при которых
выполняется условие неравенства.
Найденный
отрезок является решением для переменной t:
Однако,
цель задания найти все возможные варианты неизвестной x:
Решить
двойное неравенство достаточно просто, нужно перенести π/3 в крайние части
уравнения и произвести требуемые вычисления:
Ответ
на задание будет
выглядеть как интервал для строгого неравенства:
18 ноября 2021 г.
Тема: Решение показательных и
логарифмических неравенств. Основные приемы их решений.
Напомним, что решение простейших показательных
неравенств основано на свойствах монотонности показательной
функции ![]() , где
, где ![]() ,
, ![]() .
.
Если ![]() , то функция
, то функция ![]() является возрастающей.
является возрастающей.
Тогда показательное неравенство ![]() .
.
Если ![]() , то функция
, то функция ![]() является убывающей.
является убывающей.
Решение логарифмических
неравенств основано на свойствах монотонности логарифмической функции.
при ![]() равносильны системе
неравенств:
равносильны системе
неравенств:
при ![]() равносильны системе
неравенств:
равносильны системе
неравенств:
Мы с вами повторили основные моменты, а теперь давайте перейдём к
практической части занятия.
Задание
первое. Решите неравенства:
Решение.
Задание
второе. Решите неравенства:
Решение.
Задание
третье. Решите неравенства:
Решение.
Задание
четвёртое. Решите неравенства:
Решение.
17 ноября 2021 г.
Тема: Рациональные и
иррациональные неравенства. Метод интервалов.
При решении неравенств вы должны свободно владеть понятием числового
неравенства, знать, что такое решение неравенства, что значит решить
неравенство, помнить свойства неравенств. То же относится и к системам числовых
неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в
вузы.
Напомним свойства числовых неравенств.
1. Если а > b , то b < а; наоборот, если а
< b, то b > а.
2. Если а > b и b > c, то а > c. Точно
так же, если а < b и b < c, то а < c.
3. Если а > b, то а + c > b+ c (и а –
c > b – c). Если же а < b, то а + c < b+ c (и а – c < b – c). Т. е.
к обеим частям неравенства можно прибавлять (или из них вычесть) одну и ту же
величину.
4. Если а > b и c > d, то а + c > b + d;
точно так же, если а < b и c < d, то а + c < b + d, т. е. два
неравенства одинакового смысла можно почленно складывать.
Замечание. Два неравенства одинакового смысла нельзя
почленно вычитать друг из друга, так как результат может быть верным, но может
быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть
неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из
неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное
неравенство будет неверным.
5. Если а > b и c < d, то а – c > b – d;
если а < b и c > d, то а – c < b – d, т.е. из одного неравенства можно
почленно вычесть другое неравенство противоположного смысла, оставляя знак того
неравенства, из которого вычиталось другое.
6. Если а > b и m – положительное число, то m а
> m b и  , т.е. обе части неравенства можно
умножить или разделить на одно и то же положительное число ( знак неравенства
остаётся тем же ).
, т.е. обе части неравенства можно
умножить или разделить на одно и то же положительное число ( знак неравенства
остаётся тем же ).
Если же а > b и n – отрицательное число, то n а <
n b и ![]() , т.е. обе части неравенства можно
умножить или разделить на одно и то же отрицательное число, но при этом знак
неравенства нужно переменить на противоположный.
, т.е. обе части неравенства можно
умножить или разделить на одно и то же отрицательное число, но при этом знак
неравенства нужно переменить на противоположный.
7. Если а > b и c > d , где а, b, c, d >
0, то а c > b d и если а < b и c < d, где а, b, c, d > 0, то аc
< bd, т.е. неравенства одного смысла на множестве положительных чисел можно
почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а2 >
b2, и если а < b, то а2 < b2, т.е.
на множестве положительных чисел обе части неравенства можно возводить в
квадрат.
8. Если а > b, где а, b > 0, то ![]() и если а < b , то
и если а < b , то 
.
Виды неравенств и
способы их решения
1. Линейные
неравенства и системы неравенств
Пример 1. Решить неравенство ![]() .
.
Решение:
Пример 2. Решить систему неравенств
Решение:
Пример 3. Найти наименьшее целое решение системы неравенств
Решение:
Ответ:
Пример 4. Решить неравенство х2 > 4.
Решение:
х2 >
4 (х – 2)∙(х + 2) > 0.
Решаем методом интервалов.
3. Неравенства высших
степеней
Пример 5. Решить неравенство (х + 3)∙(х2 – 2х + 1) >
0.
Решение:
Ответ:
Пример 6. Найти середину отрезка, который является решением неравенства 4х2 – 24х + 24 < 4у2, где
Решение:
Область определения
неравенства: ![]() .
.
С учётом области определения 4х2 –
24х + 24 < 4у2 будет равносильно неравенству
Решаем методом интервалов.
Решение неравенства:
.
Середина отрезка:
.
Ответ:
.4. Рациональные неравенства
Пример 7. Найти все целые решения, удовлетворяющие неравенству ![]() .
.
Решение:
![]()
Методом интервалов:
Решение неравенства: ![]()
.
Целые числа, принадлежащие
полученным полуинтервалам: – 6; – 5; – 4; 1.
Ответ: – 6; – 5; – 4; 1.
Помните! Начинать решение иррациональных неравенств нужно с нахождения области
определения.
Пример 8. Решить неравенство ![]() .
.
Решение:
Область определения: ![]() .
.
Так как арифметический корень
не может быть отрицательным числом, то
Пример 9. Найти все целые решения неравенства ![]() .
.
Решение:
![]() – быть отрицательным не может,
следовательно, чтобы произведение было неотрицательным достаточно потребовать
выполнения неравенства
– быть отрицательным не может,
следовательно, чтобы произведение было неотрицательным достаточно потребовать
выполнения неравенства ![]() , при этом учитывая область
определения. Т.е. исходное неравенство равносильно системе
, при этом учитывая область
определения. Т.е. исходное неравенство равносильно системе
Целыми числами из этого отрезка будут
2; 3; 4.
Ответ: 2; 3; 4.
Пример 10. Решить неравенство ![]() .
.
Решение:
Область определения: 
Преобразуем неравенство: ![]() . С учётом области определения
видим, что обе части неравенства - положительные числа. Возведём обе
части в квадрат и получим неравенство, равносильное исходному.
. С учётом области определения
видим, что обе части неравенства - положительные числа. Возведём обе
части в квадрат и получим неравенство, равносильное исходному.
![]() т.е.
т.е. ![]() , и этот числовой отрезок включён в
область определения.
, и этот числовой отрезок включён в
область определения.
Пример 11. Решить неравенство ![]() .
.
Решение:
Раскрываем знак модуля.
Объединим решения систем 1) и 2):
 .
.
13 ноября 2021 г.
Тема: Решение уравнений и
систем уравнений различных видов. Практическое занятие №11.
Определение 1. Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют
равносильными, если множества их корней совпадают.
Определение 2. Если каждый корень уравнения f(x)=g(x) является в тоже время корнем
уравнения p(x)=h(x), то уравнение второе
называют следствием уравнения.
Решение любого уравнения проходит в три этапа:
1: − технический. На этом этапе проводятся
преобразования, ведущие к нахождению корня.
2: − анализ решения. Анализируя проведённые
преобразования, отвечают на вопрос об отборе корней и их количестве.
3: − проверка.
Иногда при решении уравнений происходит потеря корней.
Есть 2 причины:
1) деление
обеих частей уравнения на одно и тоже число;
2) сужение
ОДЗ в процессе решение уравнения.
Рассмотрим общие методы решения уравнений.
1. Замена уравнения h(f(x)) = h(g(x)) уравнением f(x)=g(x).
Этот метод применяем:
- при решении показательных уравнений, когда переходим
от уравнения ![]() к уравнению f(x)=g(x);
к уравнению f(x)=g(x);
- при решении логарифмических уравнений, когда
переходили от уравнения loga f(x)
= ![]() loga g(x) к
уравнению f(x)=g(x);
loga g(x) к
уравнению f(x)=g(x);
- при решении иррациональных уравнений, когда переходили от уравнения
Этот метод можно применять только в том случае,
когда y=h(x) − монотонная функция, которая каждое своё
значение принимает по одному разу.
2. Метод разложения на множители.
Суть этого метода заключается в следующем:
уравнение f(x)g(x)h(x) = 0 можно заменить
совокупностью уравнений f(x)=0; g(x)=0; h(x)=0.
Решив уравнения этой совокупности, нужно взять те
корни, которые принадлежат области определения, а остальные отбросите как
посторонние.
3.Метод введения новой переменной.
Если уравнение f(x)=0 удалось
преобразовать к виду p(g(x))=0, то нужно ввести новую переменную u=g(x),
решить уравнение p(u)=0,
=> g(x)=u1; g(x)=u2;
...; g(x)=un ,
где u1, u2 , ... , un −корни
уравнения p(u)=0.
4. Функционально - графический метод.
Чтобы решить графически уравнение f(x)=g(x), нужно построить графики функций y=f(x) b y=g(x) и
найти точки их пересечения. Корнями уравнения служат абсциссы этих точек.
Определение
1. Если поставлена задача - найти такие пары значений (x;y), которые одновременно удовлетворяют
уравнению p(x;y)=0 и
уравнению g(x;y)=0, то говорят, что данные
уравнения образуют систему уравнений.
Пару значений (x;y), которая
одновременно является решением первого и второго уравнения системы, называют
решением системы.
Определение 2. Две системы называются равносильными,
если они имеют одни и те же решения или решений нет.
Системы можно решить графически, методом
алгебраического сложения, методом подстановки.
При выполнении практической работы рассмотрите следующие примеры:
Пример
1.
Решить уравнения x3-7x+6=0.
Решение: x3-x-6x+6=0.
x(x2-1)-6(x-1)=0.
x(x-1)(x+1)-6(x-1)=0.
x(x-1)(x2+x-6)=0.
x-1=0 x2+x-6=0.
x=1 x2 =2.
x3=-3.
Ответ: 1;2;-3.
Пример 2.
Решите уравнение: cos 2x-5sin x-3=0.
Решение: u=sin x ,
cos 2x =cos2 x
- sin2 x = 1- sin2x - sin2x = 1-2u2
-2u2 -
5u-2=0. ![]()
u1 = ![]()
; u2=-2.
sin x =-2, ![]()
Пример 3.
Решение. Графики функций y=![]() и y=|x-2| постройте в одной координатной плоскости.
и y=|x-2| постройте в одной координатной плоскости.
Они пересекаются в точках А(1;1) и В(4;2)
Значит,
уравнение имеет два корня x1=1 x2=4. Ответ
: 1;4.
Пример 4.
Решить систему уравнений
Решение.
Решим способом подстановки:
Ответ: (-7;3)(1;-1)
12 ноября 2021 г.
Тема: Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность систем.
Основные методы решения систем уравнений:
1. Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
Задача. Решить систему уравнений:
Решение. Из первого уравнения системы выражаем у через х и подставляем во второе уравнение системы. Получим систему  равносильную исходной.
равносильную исходной.
После приведения подобных членов система примет вид: 
Из второго уравнения находим: ![]() . Подставив это значение в уравнение у = 2 – 2х, получим у = 3. Следовательно, решением данной системы является пара чисел
. Подставив это значение в уравнение у = 2 – 2х, получим у = 3. Следовательно, решением данной системы является пара чисел  .
.
2. Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
Задача. Решить систему уравнение:

Решение. Умножив обе части второго уравнения на 2, получим систему  равносильную исходной. Сложив два уравнения этой системы, придем к системе
равносильную исходной. Сложив два уравнения этой системы, придем к системе 
После приведения подобных членов данная система примет вид:  Из второго уравнения находим
Из второго уравнения находим ![]() . Подставив это значение в уравнение 3х + 4у = 5, получим
. Подставив это значение в уравнение 3х + 4у = 5, получим ![]() , откуда
, откуда ![]() . Следовательно, решением данной системы является пара чисел
. Следовательно, решением данной системы является пара чисел  .
.
3. Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
Задача. Решить систему уравнений:

Решение. Запишем данную систему иначе: 
Пусть х + у = u, ху = v. Тогда получим систему 
Решим ее методом подстановки. Из первого уравнения системы выразим u через v и подставим во второе уравнение системы. Получим систему  т.е.
т.е. 
Из второго уравнение системы находим v1 = 2, v2 = 3.
Подставив эти значения в уравнение u = 5 – v, получим u1 = 3,
u2 = 2. Тогда имеем две системы 

Решая первую систему, получим две пары чисел (1; 2), (2; 1). Вторая система решений не имеет.
11 ноября 2021 г.
Тема: Решение уравнений различных видов.
Методы решения тригонометрических уравнений.
1. Алгебраический метод.
( метод замены переменной и подстановки ).
2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е . Перенесём все члены уравнения влево:
sin x + cos x – 1 = 0 ,
преобразуем и разложим на множители выражение в
левой части уравнения:
П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.
Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
sin x · cos x – sin 2 x = 0 ,
sin x · ( cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1.
Р е ш е н и е . cos 2x + cos 6x = 1 + cos 8x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
cos 4x · ( cos 2x – cos 4x ) = 0 ,
cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
4. Переход к половинному углу.
П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =
= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,
2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,
tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,
. . . . . . . . . .
5. Введение вспомогательного угла.
a sin x + b cos x = c ,
где a, b, c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin
( здесь
- так называемый вспомогательный угол ), и наше уравнение принимает вид:
6. Преобразование произведения в сумму.
П р и м е р . Решить уравнение: 2 sin x · sin 3x = cos 4x.
Р е ш е н и е . Преобразуем левую часть в сумму:
cos 4x – cos 8x = cos 4x ,
cos 8x = 0 ,
8x = p / 2 + pk ,
x = p / 16 + pk / 8 .
7. Универсальная подстановка.
П р и м е р . Решить уравнение: 3 sin x – 4 cos x = 3 .
Таким образом, решение даёт только первый случай.
21 октября 2021 г.
Тема: Тригонометрические уравнения.
Простейшие тригонометрические уравнения.
20 октября 2021 г.
Тема: Показательные уравнения,
приемы их решения. Логарифмические уравнения, приемы их решения.
Напомним,
что показательным называется уравнение, содержащее переменные только
в показателе степени.
Уравнение ![]() , где
, где ![]() и
и ![]() , называется простейшим показательным.
, называется простейшим показательным.
Если ![]() , то уравнение имеет единственное
решение
, то уравнение имеет единственное
решение ![]() .
.
Если ![]() , то уравнение не имеет корней.
, то уравнение не имеет корней.
Решение
показательных уравнений основано на свойстве степеней: две степени с одним
и тем же положительным и отличным от единицы основанием равны тогда и только
тогда, когда равны их показатели.
Давайте
рассмотрим некоторые виды показательных уравнений и методы их решения.
1.
Приведение обеих частей уравнения к одному основанию ![]() .
.
равносильно уравнению
Решение.
2.
Вынесение общего множителя за скобки в уравнениях, в левой части которых
записана сумма или разность степеней с одним основанием.
Например,
Причём,
если ![]() , выносится степень с меньшим
показателем, если
, выносится степень с меньшим
показателем, если
Решите уравнение
Решение.
3.
Уравнения вида![]() ,где
,где ![]() ,
, ![]() ,
, ![]() – некоторые числа,
причём
– некоторые числа,
причём ![]() ,
, ![]() и
и ![]() , сводятся к решению квадратного
уравнения
, сводятся к решению квадратного
уравнения ![]() (или уравнения более высокой
степени) при помощи замены
(или уравнения более высокой
степени) при помощи замены ![]() при
при ![]() .
.
Решение.
А
теперь перейдём к логарифмическим уравнениям. Напомним,
что логарифмическим называется уравнение, содержащее переменные
только под знаком логарифма.
Давайте
рассмотрим основные виды логарифмических уравнений и методы их решения.
1. Логарифмические
уравнения, решаемые по определению логарифма.
Уравнение
вида ![]() при
при ![]() ,
, ![]() и
и ![]()
равносильно уравнению ![]() .
.
Решение.
ДЕВЧЕНКИ! ГДЕ КОНТРОЛЬНАЯ РАБОТА ОТ 13 ОКТЯБРЯ? ЖДУ ОТВЕТЫ НА ПОЧТУ!
15 октября 2021 г.
Тема: Иррациональные
уравнения. Основные приемы их решения.
Уравнения,
в которых под знаком корня содержится переменная, называют иррациональными.
Методы
решения иррациональных уравнений, как правило, основаны на возможности замены
(с помощью некоторых преобразований) иррационального уравнения рациональным
уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо
является его следствием. Чаще всего обе части уравнения возводят в одну и ту же
степень. При этом получается уравнение, являющееся следствием исходного.
При
решении иррациональных уравнений необходимо учитывать следующее:
1)
если показатель корня - четное число, то подкоренное выражение должно быть
неотрицательно; при этом значение корня также является неотрицательным (определение
корня с четным показателем степени);
2)
если показатель корня - нечетное число, то подкоренное выражение может быть
любым действительным числом; в этом случае знак корня совпадает со знаком
подкоренного выражения.
Пример 1. Решить
уравнение![]()
Решение.
Возведем
обе части уравнения в квадрат.
x2 - 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных
слагаемых.
x2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем
проверку полученных корней, для этого произведем подстановку значений
переменной x в исходное уравнение.
Проверка.
При x1 = -2 ![]() - истинно:
- истинно:
При x2 = -2![]() - истинно.
- истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два
корня -2 и 2.
Это
уравнение можно решить по такой же методике как и в первом примере, но мы
поступим иначе.
Найдем
ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном
уравнении одновременно должны выполнятся два условия:
Ответ:
корней нет.
Пример 3. Решить
уравнение![]() =
=![]() + 2
+ 2![]() .
.
Решение.
Нахождение
ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе
части уравнения в квадрат:
x3 + 4x - 1 - 8![]() = x3 - 1 +
4
= x3 - 1 +
4![]()
![]()
![]() + 4x;
+ 4x;
Произведя проверку устанавливаем, что x2=0 лишний корень.
Ответ: x1=1.
Пример 4. Решить
уравнение x =![]() .
.
Решение.
В
этом примере ОДЗ найти легко. ОДЗ этого уравнения: x![]() [-1;
[-1;![]() ).
).
Возведем
обе части этого уравнения в квадрат, в результате получим уравнение x2= x + 1.
Корни этого уравнения:
x2 =![]()
Произвести
проверку найденных корней трудно. Но, несмотря на то, что оба корня принадлежат
ОДЗ утверждать, что оба корня являются корнями исходного уравнения нельзя. Это
приведет к ошибке. В данном случае иррациональное уравнение равносильно
совокупности двух неравенств и одного уравнения:
x
+ 1![]() 0 и x
0 и x![]() 0 и x2 =
x + 1, из которой следует, что отрицательный корень для иррационального
уравнения является посторонним и его нужно отбросить.
0 и x2 =
x + 1, из которой следует, что отрицательный корень для иррационального
уравнения является посторонним и его нужно отбросить.
Ответ:![]()
Пример 5 . Решить
уравнение![]() +
+![]() = 7.
= 7.
Решение.
Возведем
обе части уравнения в квадрат и выполним приведение подобных членов,
перенес слагаемых из одной части равенства в другую и умножение обеих частей на
0,5. В результате мы получим уравнение
![]()
![]()
![]() = 12, (*)
являющееся следствием исходного. Снова возведем обе части уравнения в квадрат.
Получим уравнение (х + 5)(20 - х) = 144, являющееся следствием исходного.
Полученное уравнение приводится к виду x2 - 15x + 44 =0.
= 12, (*)
являющееся следствием исходного. Снова возведем обе части уравнения в квадрат.
Получим уравнение (х + 5)(20 - х) = 144, являющееся следствием исходного.
Полученное уравнение приводится к виду x2 - 15x + 44 =0.
Это
уравнение (также являющееся следствием исходного) имеет корни x1 = 4,
х2 = 11. Оба корня, как показывает проверка, удовлетворяют исходному
уравнению.
Отв.
х1 = 4, х2= 11.
Замечание.
При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (*)
производят перемножение подкоренных выражений, т. е. вместо уравнения ![]() •
•![]() = 12, пишут
уравнение
= 12, пишут
уравнение![]() = 12. Это
не приводит к ошибкам, поскольку уравнения являются следствиями
уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение
подкоренных выражений дает неравносильные уравнения.
= 12. Это
не приводит к ошибкам, поскольку уравнения являются следствиями
уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение
подкоренных выражений дает неравносильные уравнения.
В
рассмотренных выше примерах можно было сначала перенести один из радикалов в
правую часть уравнения. Тогда в левой части уравнения останется один радикал и
после возведения обеих частей уравнения в квадрат в левой части уравнения
получится рациональная функция. Такой прием (уединение радикала) довольно часто
применяется при решении иррациональных уравнений.
Пример 6. Решить
уравнение![]() -
-![]() = 3.
= 3.
Решение.
Уединив первый радикал, получаем уравнение
Возводя обе части этого уравнения в квадрат, получаем уравнение
x2 + 5x + 2 = x2 - 3x + 3 + 6![]() , равносильное
уравнению
, равносильное
уравнению
4x - 5 = 3![]() (*). Это
уравнение является следствием исходного уравнения. Возводя обе части уравнения
в квадрат, приходим к уравнению
(*). Это
уравнение является следствием исходного уравнения. Возводя обе части уравнения
в квадрат, приходим к уравнению
16x2 - 40x + 25 = 9(x2 - Зх + 3), или
7x2 -
13x - 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного
уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному
уравнению, а второй x2 =![]() - не
удовлетворяет.
- не
удовлетворяет.
Ответ:
x = 2.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе
части исходного уравнения в квадрат нам бы пришлось выполнить довольно
громозкие преобразования.
При решении иррациональных уравнений,
кроме уединения радикалов используют и другие методы. Рассмотрим пример
использования метода замены неизвестного (метод введения вспомогательной
переменной).
Пример 7. Решить
уравнение 2x2 - 6x +![]() + 2 = 0.
+ 2 = 0.
Решение.
Введем вспомогательную переменную. Пусть y =![]() , где
, где
y![]() 0, тогда получим
уравнение 2y2 + y - 10 = 0;
0, тогда получим
уравнение 2y2 + y - 10 = 0;
y1 = 2; y2 = -![]() . Второй корень
не удовлетворяет условию y
. Второй корень
не удовлетворяет условию y![]() 0.
0.
Возвращаемся к x:![]() = 2;
= 2;
x2 - 3x + 6 = 4;
x2 -3x + 2 = 0;
x1 = 1; x2 = 2. Проверкой устанавливаем, что оба корня являются
корнями исходного уравнения.
Ответ: x1 = 1; x2 = 2.
Пример 8. Решить уравнение +
+ =
=![]()
Решение.
Положим = t, Тогда
уравнение примет вид t +
= t, Тогда
уравнение примет вид t +![]() =
=![]()
откуда получаем
следствие: 2t2 - 5t + 2 = 0 Решая это квадратное уравнение, находим два
корня: t1 = 2 t2 =![]() . Задача
сводится теперь к решению следующих двух уравнений:
. Задача
сводится теперь к решению следующих двух уравнений: = 2,(*)
= 2,(*) =
=![]() (**)
(**)
Возводя обе части уравнения (*) в куб, получаем 12 - 2x = 8x - 8; x1 = 2.
Аналогично, решив (**), находим x2 =![]() .
.
Оба найденных корня удовлетворяют исходному уравнению, так как в процессе
решения мы использовали (кроме замены неизвестного) только преобразование вида
[f(x) = g(x)]![]() [fn(x) = gn(x)],
а при таком преобразовании, как было отмечено выше, получается равносильное
уравнение.
[fn(x) = gn(x)],
а при таком преобразовании, как было отмечено выше, получается равносильное
уравнение.
14 октября 2021г.
Тема: Равносильность
уравнений. Рациональные уравнения. Основные приемы их решения.
Определение 1. Уравнением с одной
переменной x называется выражение
f(x)=g(x) (1), содержащее
переменную величину x и знак равенства.
Среди видов уравнений различают алгебраические,
параметрические, трансцендентные, функциональные, дифференциальные и другие виды
уравнений.
К алгебраическим уравнениям относятся:
- линейное уравнение ax + b = 0.
- квадратное уравнение - ax2 + bx + c
= 0.
- кубическое уравнение - ax3 + bx2 + cx + d = 0.
- уравнения четвертой степени - ax4 + bx3 + cх2 +
dx + e = 0.
ax4 + bx2 + c = 0. (биквадратное)
Определение 2.
Число a называется корнем (или решением) уравнения
(1), если при подстановке этого числа в уравнение получается верное числовое равенство.
Приведя подобные, получим: 9x2–3x –6 = 0.
Определение 3. Решить уравнение – значит найти все его
корни или доказать, что их нет.
Определение 4. f(x)=g(x) иf1(x)=g1(x)
называются равносильными, если любой корень первого уравнения является
корнем второго уравнения и наоборот, или если оба эти уравнения не имеют
решений.
Решение уравнения (как действия) – это процесс, состоящий в основном в замене заданного
уравнения другим уравнением, ему равносильным. Такая замена называется тождественным
преобразованием.
Основные тождественные преобразования следующие:
1.
Замена одного
выражения другим, тождественно равным ему.
Например, уравнение (3x+2)2=15x+10 можно
заменить следующим равносильным: 9x2+12x +4 = 15x +10.
2.
Перенос членов
уравнения из одной стороны в другую с обратными знаками.
Так, в предыдущем уравнении мы можем перенести все его
члены из правой части в левую со знаком « – »: 9x2+12x+4–15x–10 = 0,
Приведя подобные слагаемые, получим: 9x2–3x –6 =
0.
3) Умножение или деление обеих частей уравнения на одно и
то же выражение (число), отличное от нуля.
Предыдущее уравнение разделим на 3, получим: ![]()
Как называется это уравнение и как его решить? (квадратное,
решается -через дискриминант
D=b2-4ac
Если D>0, то![]() -
два действительных корня.
-
два действительных корня.
Если D=0, то ![]() - один
корень или два совпадающих.
- один
корень или два совпадающих.
Если D <0, то решений нет
Очень важно, чтобы выражение, на которое мы умножаем/делим
было отлично от нуля, в противном случае новое уравнение может не быть
равносильным предыдущему, а это влечет приобретение посторонних корней или
наоборот, потери корня.
4) Возведение обеих частей уравнения в нечётную
степень или извлечение из обеих частей уравнения корня нечётной
степени.
Необходимо помнить, что:
а) возведение в чётную степень может привести к
приобретению посторонних корней;
б) неправильное извлечение корня чётной степени может
привести к потере корней.
Например, уравнение 7x = 35 имеет единственный корень x = 5
.Возведя обе части этого уравнения в квадрат, получим уравнение:
49x2 = 1225 имеющее два корня: x=5 и x =
–5. Последнее значение является посторонним корнем.
Неправильное извлечение квадратного корня из обеих частей
уравнения 49x2 = 1225 даёт в результате 7x = 35, и мы теряем
корень x = – 5.
Правильное извлечение квадратного корня приводит к
уравнению: |7x| = 35, а следовательно, к двум случаям:
1) 7x= 35, тогда x =5; 2) –7x= 35, тогда x = – 5 .
Из этих четырёх правил следует, что с помощью стандартных
приёмов и методов решения уравнений, а именно:
преобразования (раскрытие скобок, освобождение от
знаменателя, приведение подобных членов, возведение уравнения в нечетную
натуральную степень и т. д.),
разложения на множители (формально этот приём относится к
преобразованиям, но, так как он довольно часто встречается самостоятельно, мы
его выделяем особо),
введения вспомогательных неизвестных,
уравнение (1) может быть сведено к более простому и, самое
главное, равносильному уравнению f1(x)=g1(x).
13 октября 2021 г.
отрезках". Построить
прямую.
Пример 2. Найти уравнение прямой, проходящей через две точки A(1; 3) , B (2; 5) .
Пример 3. Найти уравнение прямой, проходящей через точку A (2; 4) и параллельной прямой
2x + 3y = 6.
Пример 4. Найти уравнение прямой, проходящей через точку A(1; 2; 0) , перпендикулярно плоскости 2x + y - z = 6 .
08 октября 2021 г.
Тема: Решение задач
1)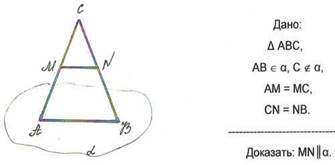
Доказательство
МN - средняя линия треугольника АВС, значит МN || АВ, АВ ![]() a .
a .
Таким образом, МN || a (по признаку параллельности прямой и плоскости).
2)На сторонах АВ и АС треугольника АВС взяты соответственно точки D и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и С и параллельна отрезку ОE. Найдите длину отрезка ВС.

Решение:
Из условия задачи № 26: треугольник АВС подобен треугольнику АDЕ.
Тогда АВ/АD = ВС/DЕ, 5/3 = х/5, х = 25/3, х = 81/3.
Ответ: 81/3.
3) Сторона АС треугольника АВС параллельна плоскости a , а стороны АВ и ВС пересекаются с этой плоскостью в точках М и N. Докажите, что треугольники АВС и МВN подобны.
Перед решением данной задачи необходимо вспомнить признаки подобия треугольников.

Доказательство
1. По утверждению : МN || АC. Тогда угол А = углу ВМN (как односторонние при параллельных прямых).
2. угол В - общий.
З. Таким образом, по двум углам треугольник АВС подобен треугольнику МВN.
Тема:
Взаимное расположение прямых и плоскостей в пространстве
Теория
Прямая на плоскости, ax + by + c = 0 ; y = kx + b ; k = tga - тангенс угла наклона
прямой к оси OX ; отрезок, отсекаемый прямой на оси OY , равен b![]()
![]()
Уравнение прямой в отрезках : x + y = 1 , где
p q
- p , q - отрезки, отсекаемые прямой на осях координат.
Уравнение пучка прямых y - y0 = k × ( x - x0 ) .
![]() Уравнение прямой,
проходящей через две точки: x - x0 x1 - x0
Уравнение прямой,
проходящей через две точки: x - x0 x1 - x0
= y - y0 ;
![]() y1 - y0
y1 - y0
Условие перпендикулярности прямых, k1 × k2 = -1 ;
Угол между прямыми,
tga=k2 - k1
![]() 1+ k1 × k2
1+ k1 × k2
Плоскость и прямая в пространстве
![]() Каноническое уравнение плоскости a × ( x - x
0 ) + b × ( y - y
0 ) + c × ( z - z 0 ) = 0 ,
Каноническое уравнение плоскости a × ( x - x
0 ) + b × ( y - y
0 ) + c × ( z - z 0 ) = 0 ,
проходящей через точку нормаль плоскости M 0 ( x 0 , y 0 , z 0 ) , перпендикулярно вектору n = (a, b, c) -нормаль плоскости
Общее уравнение
плоскости ax + by + cz + d = 0 ;
Уравнение плоскости в отрезках
x + y + z = 1 , где p ,
![]()
![]()
![]()
p q r
06 - 07 октября 2021 г.
Тема: Параллельное и ортогональное проектирование.
Изображение пространственных фигур.
В стереометрии большое значение имеет
умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда
в планиметрии на листе бумаги изображают плоскую фигуру, то все точки
изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются
фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо
знать правила, по которым изображают на плоскости пространственные фигуры.
Итак, зачастую для изображения на
плоскости (например, на листе бумаги) геометрических фигур, расположенных в
пространстве, используется параллельное проектирование.
Определяется оно следующим образом.
Пусть ![]() — некоторая плоскость, а
— некоторая плоскость, а ![]() — некоторая прямая, пересекающая эту плоскость. Возьмём
в пространстве произвольную точку
— некоторая прямая, пересекающая эту плоскость. Возьмём
в пространстве произвольную точку ![]() . Если точка
. Если точка ![]() не лежит на прямой
не лежит на прямой ![]() , то проведём через точку
, то проведём через точку ![]() прямую, параллельную прямой
прямую, параллельную прямой ![]() , и обозначим через
, и обозначим через ![]() точку пересечения этой прямой с плоскостью
точку пересечения этой прямой с плоскостью ![]() . Если же точка
. Если же точка![]() лежит на прямой
лежит на прямой![]()
![]() точку пересечения прямой
точку пересечения прямой ![]() с плоскостью
с плоскостью![]()
Точка
Плоскость![]()
![]() говорят, что она задаёт направление
проектирования.
говорят, что она задаёт направление
проектирования.
Все прямые, параллельные прямой![]()
Пусть ![]() — плоская или пространственная фигура. Проекцией
фигуры
— плоская или пространственная фигура. Проекцией
фигуры ![]() на плоскость
на плоскость ![]() при проектировании параллельно прямой
при проектировании параллельно прямой ![]()
называется множество![]()
![]() .
.
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
Вспомним основные свойства
параллельного проектирования при условии, что проектируемые отрезки и
прямые не параллельны прямой, задающей направление проектирования.
1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
2. Проекции параллельных прямых параллельны или совпадают.
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
Следствие. При параллельном проектировании
середина отрезка проектируется в середину его проекции.
При параллельном проектировании могут
искажаться размеры отрезков и углы, но обязательно сохраняется параллельность
прямых.
Если точка делит отрезок в отношении ![]() , то проекция точки будет делить проекцию отрезка также в
отношении
, то проекция точки будет делить проекцию отрезка также в
отношении ![]() .
.
Центр правильного треугольника отображается в точку пересечения медиан проекции этого треугольника, центр квадрата — в точку пересечения диагоналей проекции квадрата.
А теперь давайте поговорим об изображении
пространственных фигур.
Рассмотренные свойства параллельного
проектирования применяются при выполнении рисунков (изображений фигур),
иллюстрирующих теоремы и задачи стереометрии.
Изображением фигуры ![]() называется любая фигура, подобная проекции этой фигуры
на некоторую плоскость.
называется любая фигура, подобная проекции этой фигуры
на некоторую плоскость.
Выполняя изображения фигур, расположенных
в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном
проектировании, а в остальном изображение может быть произвольным. Важно
только, чтобы изображения рассматриваемых фигур были наглядными и давали верное
представление о них.
При различном выборе плоскости проекций и
направления проектирования получаются различные проекции данной фигуры, а
значит, и различные её изображения.
Например, вы видите фигуры, которые являются изображениями куба.
Причём изображение куба, данное на первом
рисунке, не даёт представления о кубе, наглядным является изображение, которое
дано на последнем рисунке.
При построении изображений плоских фигур,
расположенных в пространстве, предполагается, что плоскости рассматриваемых
фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.
При этом величины углов и отношение длин
непараллельных сторон не сохраняются, но при этом медианы треугольника
отображаются в медианы его проекции. В частности, за изображение
прямоугольного, равнобедренного, равностороннего треугольников можно принять
любой треугольник.
Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.
В частном случае за изображение
прямоугольника, квадрата, ромба можно принять любой параллелограмм.
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований.
Правильный шестиугольник проектируется в искажённый шестиугольник с сохранением параллельности противолежащих сторон.
Окружность проектируется в эллипс, большая ось которого имеет длину, равную диаметру окружности.
При изображении пространственных фигур пользуются тем фактом, что фигуру, состоящую из сторон и диагоналей любого выпуклого или невыпуклого четырёхугольника, можно считать изображением треугольной пирамиды при определённом выборе направления проектирования и плоскости, на которую проектируется эта пирамида.
Например, фигуры, изображённые на экране, являются изображениями треугольной пирамиды при соответствующем выборе направления проектирования.
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.
Аналогичным образом изображается прямоугольный параллелепипед.
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий её основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.
Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий её основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединить её с вершинами многоугольника. Полученные отрезки будут изображать боковые рёбра пирамиды.
Для изображения цилиндра достаточно изобразить его основания в виде двух эллипсов, получающихся друг из друга параллельным переносом, и нарисовать две образующие, соединяющие соответствующие точки этих оснований.
Для изображения конуса достаточно изобразить его основание в виде эллипса, отметить вершину и провести через неё две образующие, являющиеся касательными к этому эллипсу.
Основные моменты мы с вами повторили, а
теперь давайте перейдём к практической части занятия.
Задача первая. Точки ![]() и
и ![]() находятся по одну сторону от плоскости
находятся по одну сторону от плоскости ![]() . Точки
. Точки ![]() и
и ![]() — их параллельные проекции на эту плоскость,
причём
— их параллельные проекции на эту плоскость,
причём ![]() . Постройте точку пересечения
. Постройте точку пересечения ![]() прямой
прямой ![]() с плоскостью
с плоскостью ![]() . И найдите расстояние между серединой отрезка
. И найдите расстояние между серединой отрезка ![]() и её проекцией на плоскость
и её проекцией на плоскость![]()
![]() и
и ![]() см.
см.
Решение.
Задача вторая. На диагонали
Решение.
Задача вторая. На диагонали ![]() параллелепипеда
параллелепипеда![]()
![]() , а на прямой
, а на прямой ![]() – точка
– точка ![]() так, что отрезки
так, что отрезки![]()
![]() параллельны. Найти их отношение.
параллельны. Найти их отношение.
Решение.
Уважаемые студенты! До 8 октября предоставить конспекты (можно на эл.почту), и контрольную работу!
1 октября 2021г
Тема: Двугранный угол,
линейный угол двугранного угла. Перпендикулярность плоскостей, признаки и
свойства.
Для
начала давайте вспомним, что понимали под углом в планиметрии. Итак, углом
на плоскости мы называлигеометрическую фигуру, образованную двумя лучами,
исходящими из одной точки.
В
стереометрии наряду с такими углами рассматривается еще один вид углов, которые
называют двугранными углами. Но прежде чем мы введем понятие двугранного угла,
давайте вспомним одну из аксиом планиметрии: «любая прямая, проведенная в
данной плоскости, разделяет эту плоскость на две полуплоскости».
Пусть есть прямая а, которая лежит в некоторой плоскости. Тогда можно указать две части этой плоскости, каждая из которых вместе с прямой а называется полуплоскостью.
Прямая
а называется границей для каждой из полуплоскостей. В отличие от планиметрии, в
пространстве две полуплоскости с общей границей прямой а, могут не лежать в
одной плоскости.
Давайте
представим себе, что мы перегнули плоскость по прямой а так, что две
полуплоскости с границей а оказались уже не лежащими в одной плоскости.
Полученная фигура и есть двугранный угол.
Определение. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Полуплоскости,
образующие двугранный угол, называются его гранями. У двугранного
угла две грани, отсюда и название – двугранный угол.
Прямая
а – общая граница полуплоскостей – называется ребром двугранного угла.
Двугранный
угол, ребро которого есть прямая AB, а гранями являются полуплоскости α и β,
обозначают так![]()
Или,
если двугранный угол с ребром AB, на разных гранях которого отмечены точки C и
D, то двугранный угол называют CABD.
В
обыденной жизни мы часто встречаемся с предметами, имеющими форму двугранного
угла. Представление о двугранном угле нам дают: полураскрытая книга, открытый
ноутбук, двускатная крыша здания, стена комнаты совместно с полом и т.д.
Напомню,
что углы на плоскости измеряются в градусах.
Для измерения двугранного угла вводится понятие линейного угла. Пусть точка О лежит на ребре l двугранного угла. В каждой грани из этой точки проведем лучи ОА и ОB перпендикулярно к ребру l. Угол АОB, сторонами которого служат лучи ОА и ОB, называется линейным углом данного двугранного угла.
Определение. Линейным
углом двугранного угла называется угол, сторонами которого являются лучи с
общим началом на ребре двугранного угла, которые проведены в его гранях
перпендикулярно ребру.
На
рисунке вы видите изображение линейного угла AOB двугранного угла с
ребром l. Так как ОА перпендикулярно l и ОB
перпендикулярно l, то плоскость, в которой лежат лучи ОА и ОB,
перпендикулярна к прямой l. Таким образом, плоскость линейного угла
перпендикулярна к ребру двугранного угла. Очевидно, двугранный угол имеет
бесконечное множество линейных углов.
Верно
следующее утверждение: все линейные углы двугранного угла равны между
собой.
Докажем
это утверждение.
Рассмотрим два линейных угла А О Б и А один О один Б один двугранного угла,ребро которого эль. Лучи ОА и О один А один лежат в одной грани и перпендикулярны ребру эль. Следовательно, они параллельны. Аналогично и лучи ОБ и О один Б один лежат в одной грани и перпендикулярны ребру эль. Значит, они параллельны.
Отложим
на лучах ОА и О1A1 равные отрезки OM и O1M1 соответственно, а на
лучах ОB и O1B1 – равные отрезки ON и O1N1 соответственно.
Так
как OM равно O1M1 и OM параллельно O1M1, то четырехугольник OMM1O1 –
параллелограмм. Тогда ОО1 равно MM1 и OO1 параллельно
MM1 по свойствам параллелограмма.
Так
как ON равно O1N1 и ON параллельно O1N1, то четырехугольник ONN1O1 –
параллелограмм. Тогда OO1 равно NN1 и OO1 параллельно
NN1 по свойствам параллелограмма. Отсюда, OO1 равно NN1 и
OO1 параллельно NN1.
Видим,
что тогда MM1 равно NN1 и MM1 один параллельно NN1, т.е.
четырехугольник NMM1N1 – параллелограмм. Следовательно, NM равно N1M1.
Рассмотрим
треугольники OMN и O1M1N1. Они равны по трем сторонам. Отсюда следует, что угол
MON равен углу M1O1N1. А значит, и угол АОB равен углу A1O1B1. Что и
требовалось доказать.
Это
утверждение можно доказать и быстрее. Достаточно было при рассмотрении линейных
углов AOB и A1O1B1 заметить, что так как лучи ОА и O1A1 лежат в
одной грани и перпендикулярны к прямой OO1, то они параллельны, а, значит
сонаправлены. Точно также лучи ОB и O1B1 лежат в одной грани и
перпендикулярны к прямой OO1, следовательно они параллельны, и, значит сонаправлены.
Отсюда вытекает, что угол A1O1B1 равен углу AOB (как углы с
сонаправленными сторонами). Что и требовалось доказать.
Определение. Градусной
мерой двугранного угла называется градусная мера его линейного угла.
Это говорит о том, что, сколько градусов содержится в линейном угле, столько же градусов содержится в его двугранном угле.
На
рисунке вы видите изображение двугранного угла, градусная мера которого равна
50°. Обычно говорят коротко: «Двугранный угол равен 50°».
Различают следующие
виды двугранных углов.
Двугранный
угол называется прямым, если его линейный угол равен 90°.
Двугранный
угол называется острым, если его линейный угол острый, т.е. < 90°
(расположен в промежутке от 0 до 90 градусов).
Двугранный угол называется тупым, если его линейный угол тупой, т.е. > 90° (расположен в промежутке от 90 до 180 градусов).
Если
грани двугранного угла лежат в одной плоскости, то он
называется развернутым.
В
дальнейшем под двугранным углом будем понимать всегда тот, линейный угол φ
которого удовлетворяет условию 0°<φ<180°.
Рассмотрим
примеры.
Пусть ABCDA1B1C1D1 – прямоугольный параллелепипед. Тогда угол ADD1 является линейным углом двугранного угла, ребро которого есть прямая DC, а его грани – полуплоскости, в которых лежат прямоугольники ABCD и DCC1D1, так как АD перпендикулярно DC и DD1 перпендикулярно DC. Угол ADD1 – прямой, следовательно, указанный двугранный угол – прямой.
Двугранным
углом при ребре пирамиды называется двугранный угол, ребро которого содержит
ребро пирамиды. А грани двугранного угла содержат грани пирамиды, которые
пересекаются по данному ребру пирамиды.
Пусть DABC – правильная треугольная пирамида, а точка О – середина ребра АC. Прямая DО перпендикулярна прямой АС.
Так
как медиана в равностороннем треугольнике ABC является и высотой. Прямая BО
также перпендикулярна прямой АС. Так как медиана в равнобедренном треугольнике
DAC является и высотой. Значит, угол DOB есть линейный угол двугранного угла
DACB, ребро которого – прямая AC, а гранями являются полуплоскости, содержащие
треугольники ABC и DAC.
Подведем
итоги урока. На этом уроке мы познакомились с понятием двугранного угла.
Узнали, что двугранным углом называется фигура, образованная прямой а и двумя
полуплоскостями с общей границей а, не принадлежащими одной плоскости. Ввели
понятие линейного угла: линейным углом двугранного угла называется угол,
сторонами которого являются лучи с общим началом на ребре двугранного угла,
которые проведены в его гранях перпендикулярно ребру. А также убедились, что
градусной мерой двугранного угла называется градусная мера его линейного угла
и, что все линейные углы двугранного угла равны между собой.
30 сентября 2021г
Тема: Параллельность
плоскостей, признаки и свойства.
Как
известно из аксиом стереометрии, если плоскости имеют одну общую точку,
то они пересекаются по прямой, проходящей через эту точку. Значит, две
плоскости или пересекаются, или не пересекаются.
Плоскости,
которые не пересекаются, называются параллельными.
Параллельные
плоскости α и β обозначаются α∥β.
Пример:
любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
Рис. 1. Стены здания.
Признак
параллельности плоскостей.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Рис. 2.
Доказательство признака параллельности плоскостей.
Доказательство.
Пусть α и β —
данные плоскости, a1 и a2 — пересекающиеся прямые в
плоскости α, а b1 и b2 — соответственно параллельные
им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть, они пересекаются по некоторой прямой c.
Прямая a1 параллельна
прямой b1, значит, она параллельна и самой плоскости β.
Прямая a2 параллельна
прямой b2, значит, она параллельна и самой
плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит, хотя бы одна из прямых — a1 или a2 — пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из
этого следует, что плоскости α и β не пересекаются, то
есть, они параллельны.
Свойства
параллельных плоскостей
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
Рис. 3. Две параллельные плоскости пересечены третьей плоскостью..
Доказательство.
Пусть α и β —
параллельные плоскости, а γ — плоскость, пересекающая их.
Плоскость α пересекается
с плоскостью γ по прямой a.
Плоскость β пересекается
с плоскостью γ по прямой b.
Линии
пересечения a и b лежат в одной
плоскости γ и потому могут быть либо пересекающимися, либо
параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не
могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны.
Рис. 4. Параллельные прямые пересекают две параллельные плоскости.
Доказательство.
Пусть α и β —
параллельные плоскости, а a и b — параллельные прямые,
пересекающие их.
Через
прямые a и b можно провести плоскость — эти прямые
параллельны, значит, определяют плоскость, причём только одну.
Проведённая
плоскость пересекается с плоскостью α по прямой AB, а с
плоскостью β — по прямой CD.
По
предыдущей теореме прямые AB и CD параллельны.
Четырёхугольник ABCD есть параллелограмм (у него противоположные
стороны параллельны). А раз это параллелограмм, то противоположные стороны у
него равны, то есть BC=AD.
Задача. Даны
плоскости ![]() . Плоскость
. Плоскость ![]() пересекает эти плоскости по прямым
пересекает эти плоскости по прямым![]()
![]() соответственно, причем
соответственно, причем![]()
![]() . Прямая
. Прямая ![]() и пересекает прямые
и пересекает прямые![]()
![]()
![]()
![]() соответственно. Угол
соответственно. Угол ![]() . Определите чему равен
. Определите чему равен
29 сентября 2021г
Решение задач.
Задача. В ![]()
![]() , а
, а ![]() – перпендикуляр к
– перпендикуляр к
плоскости![]() . Докажите, что
. Докажите, что![]() – прямоугольный.
– прямоугольный.
Доказательство.
Задача. ![]() – куб. Точка
– куб. Точка ![]() – точка пересечения диагоналей грани
– точка пересечения диагоналей грани ![]() . Точка
. Точка ![]() – середина ребра
– середина ребра![]()
Доказательство.
Задача. Из
вершины![]() прямоугольника
прямоугольника![]() восстановлен перпендикуляр
восстановлен перпендикуляр![]() к плоскости прямоугольника. Расстояния от
точки
к плоскости прямоугольника. Расстояния от
точки ![]()
![]() см,
см, ![]() см и
см и ![]() см. Найдите длину перпендикуляра
см. Найдите длину перпендикуляра![]()
24 сентября 2021г
Тема: Теорема о трех
перпендикулярах. Перпендикуляр и наклонная.
Перпендикуляром, проведенным из точки А к плоскости α, называется отрезок AH. Точка AH называется основанием перпендикуляра. Если точка M – произвольная точка плоскости α, отличная от точки AH, то отрезок AM называется наклонной, проведенной из точки А к плоскости α, а точка М – основанием наклонной. Проекцией наклонной на плоскость, называется отрезок, соединяющий основание перпендикуляра и основание наклонной, проведенных из одной и той же точки к данной плоскости. В нашем случае, отрезок HM является проекцией наклонной AM на плоскость α.
Рассмотрим пример. Пусть ABCA1B1C1 – прямая треугольная призма. Тогда ребро B1B есть перпендикуляр, проведенный из точки B1 к плоскости ее основания ABC, отрезок B1C – наклонная, отрезок CB – проекция наклонной B1C на плоскость ABC.
Давайте сформулируем и докажем теорему, которая играет важную роль при решении многих задач.
Теорема. Прямая,
проведенная в плоскости через основание наклонной перпендикулярно к ее проекции
на эту плоскость, перпендикулярна и к самой наклонной.
Доказательство. Пусть нам дана плоскость α. Проведем перпендикуляр AH к плоскости α. Тогда AM – наклонная, точка М – основание наклонной. HM – проекция наклонной AM на плоскость α. В плоскости α проведем прямую а через основание наклонной M перпендикулярно проекции HM. Докажем, что прямая а перпендикулярна и наклонной AM.
Прямая AH – это
перпендикуляр к плоскости α по условию. Значит, прямая AH перпендикулярна и
всем прямым, лежащим в этой плоскости. А тогда прямая AH перпендикулярна и
прямой а, лежащей в плоскости α.
Прямая HM перпендикулярна
прямой а по условию. Следовательно, прямая а перпендикулярна двум
пересекающимся прямым AH и HM плоскости AHM. Тогда по признаку
перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости AHM.
Значит, прямая а перпендикулярна любой прямой, лежащей в плоскости AHM. Прямая
AM лежит в плоскости AHM. Следовательно, прямая а перпендикулярна прямой AM.
Теорема доказана.
Эта теорема называется
теоремой о трех перпендикулярах, так как в ней говорится о связи между тремя
перпендикулярами AH, HM и AM.
Что и требовалось доказать.
Справедлива также и
обратная теорема. Сформулируем и докажем ее.
Обратная теорема. Прямая, проведенная в плоскости через основание наклонной
перпендикулярно к ней, перпендикулярна и к ее проекции.
Доказательство. Пусть нам дана плоскость альфа. Проведем перпендикуляр AH к плоскости α. Тогда прямая AM – наклонная. HM – проекция наклонной AM на плоскость α. В плоскости α проведем прямую а через основание наклонной M перпендикулярно наклонной AM. Докажем, что прямая а перпендикулярна проекции HM.
Прямая AH – это перпендикуляр к плоскости α по
условию. Значит, прямая AH перпендикулярна и всем прямым, лежащим в этой
плоскости. А тогда прямая AH перпендикулярна прямой а. Прямая AM
перпендикулярна прямой а по условию. Следовательно, прямая а перпендикулярна
двум пересекающимся прямым AH и AM плоскости AHM. Тогда по признаку
перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости AHM.
Значит, прямая а перпендикулярна любой прямой, лежащей в этой плоскости. Прямая
HM лежит в плоскости AHM. Следовательно, прямая а перпендикулярна прямой
HM. Теорема доказана.
Замечание. В доказанной прямой и обратной теореме точка М (основание наклонной) лежала на прямой а, принадлежащей плоскости α. Давайте проведем в плоскости α другую прямую b, которая параллельна прямой а. Тогда углы между прямыми b, АМ, HМ не изменятся. И из перпендикулярности прямой b и прямой AМ будет вытекать перпендикулярность прямой b и HМ и наоборот.
23 сентября 2021г
Тема: Перпендикуляр и
наклонная к плоскости. Между прямой и плоскостью.
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
Определение 1 Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
Определение 2 Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
Определение 3 Проекция точки M M на плоскость γ γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ γ, проходящей через точку M M, при условии, что она не принадлежит плоскости γ γ.
Определение 4 Проекция прямой а на плоскость γ γ - это множество проекций всех точек заданной прямой на плоскость.
Отсюда получаем, что перпендикулярная к плоскости γ γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a a – это прямая, принадлежащая плоскости γ γ и проходящая через точку пересечения прямой a a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все
необходимые сведения и данные для формулировки определения угла между прямой и
плоскостью
Определение
5 Углом между прямой и плоскостью
называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая
не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью,
считается прямым, то есть равным 90 90 градусов, а угол, расположенный между
параллельными прямыми, не определяется. Бывают случаи, когда его значение
берется равным нулю.
22 сентября 2021г
Тема: Перпендикулярность
прямой и плоскости, признаки и свойства.
Перпендикулярные прямые в
пространстве
Две прямые
называются перпендикулярными, если угол между ними равен 90°.
В
пространстве перпендикулярными называют не только пересекающиеся прямые, но и
скрещивающиеся прямые, так как мы говорим об угле, который могут
образовать эти прямые, если их поместить в одной плоскости.
Так же как и
в плоскости, в пространстве перпендикулярные прямые a и b обозначают a⊥b.
Если одна из двух параллельных
прямых перпендикулярна третьей прямой, то и другая перпендикулярна этой прямой.
Перпендикулярность прямой и
плоскости
Прямая, пересекающая плоскость,
называется перпендикулярной этой плоскости, если она перпендикулярна
каждой прямой, которая лежит в данной плоскости.
Перпендикулярность
прямой и плоскости обозначается как a⊥α.
Через любую точку пространства
перпендикулярно данной плоскости проходит прямая, притом только одна.
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым в плоскости,
то она перпендикулярна этой плоскости.
Доказательство:
пусть a — прямая, перпендикулярная прямым b и c в
плоскости. Проведём прямую a через точку A пересечения прямых b и c. Докажем, что прямая a перпендикулярна
плоскости, то есть каждой прямой в этой плоскости.
1. Проведём произвольную прямую x через точку A в плоскости и покажем, что она перпендикулярна
прямой a. Проведём в плоскости произвольную прямую, не
проходящую через точку A и пересекающую
прямые b, c и x. Пусть точками пересечения будут B, C и X.
2. Отложим на прямой a от точки A в разные стороны равные отрезки AM и AN.
3. Треугольник MCN равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению (AM=AN). По той же причине треугольник MBN тоже равнобедренный.
4. Следовательно, треугольники MBC и NBC равны по трём сторонам.
5. Из
равенства треугольников MBC и NBC следует равенство углов MBX и NBX и,
следовательно, равенство треугольников MBX и NBX по двум сторонам и углу между ними.
6. Из равенства сторон MX и NX этих треугольников заключаем, что треугольник MXN равнобедренный. Поэтому его медиана XA является также высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости.
Свойства перпендикулярных прямой и плоскости.
1. Если
плоскость перпендикулярна одной из двух параллельных прямых, то она
перпендикулярна и другой.
2. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
17 сентября 2021г
Тема: Параллельность прямой и
плоскости, признаки и свойства.
Параллельные
прямые
Параллельные прямые – прямые, которые лежат в одной плоскости и не
пересекаются.
Признак
параллельности прямых
Две прямые, параллельные третьей,
параллельны между собой.
Параллельные
прямая и плоскость
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак
параллельности прямой и плоскости
Если прямая, не принадлежащая данной
плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна
этой плоскости.
Свойство прямой, параллельной данной плоскости
Если плоскость β проходит
через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.
Параллельные
плоскости
Параллельные плоскости – плоскости, которые не
пересекаются.
Признаки
параллельности плоскостей
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум пересекающимся прямым другой
плоскости, то такие плоскости параллельны.
Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.
Свойства
параллельных плоскостей
Если две параллельные плоскости
пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.
Отрезки параллельных прямых,
заключенные между двумя параллельными плоскостями, равны.
16 сентября 2021г
Тема: Взаимное расположение
двух прямых в пространстве. Угол между прямыми. Условия параллельности и
перпендикулярности двух прямых.
В пространстве мы можем найти множество примеров
ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Скрещивающиеся прямые
— это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в
некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной
плоскости).
Доказательство
Рассмотрим
прямую AB, лежащую в плоскости, и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB.
Рис. 2. Скрещивающиеся прямые.
1. Допустим,
что прямые AB и CD всё-таки лежат в
одной плоскости.
2. Значит, эта плоскость идёт через прямую AB и точку D, то есть, она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, по которым прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными.
Рис. 3. Параллельные прямые.
Рис. 4. Пересекающиеся прямые.
Рис. 5. Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся
прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим
скрещивающиеся прямые AB и CD.
Рис. 6. Доказательство теоремы.
1. Через точку D можно провести прямую DE, параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α.
3. Так как прямая AB не лежит в этой плоскости и
параллельна прямой DE, то она параллельна плоскости.
4. Эта
плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.
Угол между прямыми. Условия
параллельности и перпендикулярности двух прямых
Угол ![]() между пересекающимися прямыми определяется по формуле
между пересекающимися прямыми определяется по формуле
При этом под
углом ![]() понимается угол, на который надо
повернуть первую прямую, заданную параметрами
понимается угол, на который надо
повернуть первую прямую, заданную параметрами
Прямые
перпендикулярны, если ![]() или
или![]()
Любую
прямую, параллельную ![]() , можно выразить уравнением
, можно выразить уравнением![]() , при этом расстояние между ними
будет равно
, при этом расстояние между ними
будет равно
Если знак
перед радикалом противоположен ![]() то
то![]() будет положительным, когда вторая прямая
и начало координат лежат по разные стороны от первой прямой.
будет положительным, когда вторая прямая
и начало координат лежат по разные стороны от первой прямой.
Для того,
чтобы три прямые
пересекались
в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы
выполнялось условие
перпендикулярны.
Рассмотрим
пример. Две прямые
заданы уравнениями
найти угол
между данными прямыми.
Рассмотрим
пример. Задана
прямая
Составить
для этой прямой уравнение в отрезках и при желании построить ее.
Преобразуем
исходное уравнение прямой
разделим обе
части уравнения на (-15)
15 сентября 2021г
Тема: Основные понятия стереометрии (точка, прямая,
плоскость, пространство). Аксиомы стереометрии и следствие из них. Понятие об
аксиоматическом способе построения геометрии.
Основные
фигуры в пространстве: точки, прямые и плоскости.
Основные
свойства точек, прямых и плоскостей, касающиеся их взаимного расположения,
выражены в аксиомах.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость,
и притом только одна.
|
|
|
|
рис.
4 |
А2. Если
две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
|
|
АB |
|
рис.
5 |
Замечание. Если
прямая и плоскость имеют только одну общую точку, то говорят, что они
пересекаются.
|
|
а |
|
рис.
6 |
А3. Если
две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
все общие точки этих плоскостей.
|
|
|
|
рис.
7 |
Следствие
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом
только одна.
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом
только одна.
Обратите
внимание на данные фигуры. Как вы заметили- они объемные.
И
их все объединяет раздел геометрии Стереометрия.
Что
же такое стереометрия?
По
аналогии с планиметрией мы можем вывести следующее определение:
Стереометрия-
это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Простейшими
(основными) фигурами в пространстве являются точки, прямые и плоскости.
Изучая
свойства геометрических фигур, мы получаем представления о геометрических
свойствах реальных предметов. В этом и состоит практическое значение геометрии,
в частности стереометрия, широко используется в строительстве, архитектуре,
машиностроении, геодезии, в науке и технике.
В
планиметрии основными фигурами были точки и прямые. В стереометрии наряду с
ними рассматривается ещё одна основная фигура – плоскость.
Представление
плоскости нам дает любая гладкая поверхность. Она безгранична.
В
стереометрии:
точки
обозначаются прописными латинскими буквами: А, В, С и т. д.
прямые
– строчными латинскими буквами: а, b, с и т. д. или двумя большими латинскими
буквами: АВ, ВС и т. д.
плоскости
– греческими буквами: α, β, γ и т. д.
Основные
свойства точек, прямых и плоскостей, касающиеся их взаимного расположения,
выражены в аксиомах.
А1: Через
3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Точки А ![]() α, В
α, В ![]() α, С
α, С ![]() α.
α.
Если
взять четыре произвольные точки, то через них может не проходить ни одна
плоскость.
А2: Если
две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
В
этом случае говорят, что прямая лежит в плоскости или плоскость проходит через
прямую.
Это
свойство используется при проверке “ровности” линейки.
Если
прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
А3: Если
две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
все общие точки этих плоскостей.
В
этом случае говорят, что плоскости пересекаются по прямой.
Пример: пересечение
пола и стены
В
пространстве существует бесконечно много плоскостей, и в каждой плоскости
справедливы все аксиомы и теоремы планиметрии.
Некоторые
следствия из аксиом.
Теорема
1: Через прямую и не лежащую на ней точку проходит плоскость, и притом
только одна.
Дано:
а – прямая, точка М ∉
а.
Доказать:
1) существует α: а ![]() α.
α.
2)
α – единственная.
Доказательство:
1)
Дополнительные построения: т. В ![]() а, т. С
а, т. С ![]() а.
а.
2)
В, С, М не лежат на одной прямой, следовательно, по первой аксиоме существует
плоскость α.
3)
т. к.
4)
Единственность α. следует из того, что любая плоскость, проходящая через прямую
а и т. М, проходит через М, В, С. Значит, она совпадает с α (по Аксиоме 1).
Теорема доказана.
Теорема
2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.
Дано:
а ∩ b в точке М
Доказать:
существование плоскости α, а ![]() α, b
α, b ![]() α.
α.
Доказательство:
1)
Дополнительные построения: N Є b, N∉
a.
2)
Существует α : N ![]() α, a
α, a ![]() α.
α.
3)
4)
Из 2) и 3) следует α. проходит через прямые а и b.
5)
Единственность α следует из того, что любая плоскость, проходящая через прямые
а и b, проходит через точку N, значит она совпадает с α (по Теореме 1). Теорема
доказана.
10 сентября 2021г
Тема: Теорема Пифагора, теорема косинусов.
Знать эту теорему НЕОБХОДИМО. Что мы можем
найти, используя её?
Если нам будут известны две стороны и угол
между ними, мы без труда найдём третью сторону. Для этого нужно просто
подставить в формулу известные величины. Для других сторон всё то же самое:
Можно ли использовать теорему косинусов
для нахождения третьей стороны, если известны любые две стороны и угол,
не лежащий между этими сторонами? Например, нам известны стороны a и b и угол
альфа. Тогда из формулы
мы можем найти сторону «с». Приводим
к виду:
То есть, мы получаем квадратное уравнение
с переменной «с» (все остальные величины нам известны). Решив его, получим
искомую сторону.
Мы можем найти любой угол, если нам
известны все три стороны треугольника:
Разумеется, что учить все эти
формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А
косинус любого угла не трудно выразить используя простые алгебраические
преобразования.
*Если вы вычисляете косинус
тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так
как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах
получите положительное значение, то ищите ошибку.
Следующий вопрос: а если нам
дана сторона и любые два угла, что делать? В этом случае теорема косинусов не
используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из
следующих статей, не пропустите!
Если вы будете в
совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением
треугольников (в большинстве задач).
Следующий факт знают все, но
всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать
стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то
получим:
То есть, по сути, теорема
Пифагора это как бы частный случай теоремы косинусов.
Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:
По теореме косинусов:
Так как угол С равен 90, то
Напомню, что зная любые две
стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без
труда можем найти значение любой тригонометрической функции острого угла
в нём.
9 сентября 2021г
Тема: Геометрия на плоскости.
Треугольник его виды, элементы. Формулы площади треугольника. Формулы Герона,
выражение площадей треугольника через радиус вписанной и описанной окружностей.
Итак, чтобы найти площадь треугольника, зная длины его сторон, удобно использовать формулу, которая называется формулой Герона (по фамилии ученого, который включил ее в свой труд «Метрика»):
Например,
если стороны треугольника равны ![]() (см. рис. 28), то его площадь легко вычислить
с использованием формулы Герона:
(см. рис. 28), то его площадь легко вычислить
с использованием формулы Герона:
Использование
этой теоремы, как вы видели, совсем не сложно. А вот доказательство достаточно
длинное. С ним вы можете ознакомиться ниже.
Доказательство
формулы Герона
Доказательство.
Рассмотрим
треугольник ![]() со сторонами
со сторонами ![]() (см. рис. 29).
(см. рис. 29).
 Рис.
29. Произвольный треугольник
Рис.
29. Произвольный треугольник У нас есть формула для площади треугольника:
Наша
задача – выразить ![]() через
через ![]() . Обозначим для краткости (см. рис. 30):
. Обозначим для краткости (см. рис. 30):
Откуда:
Теперь
можем выразить из треугольника![]()
![]() через
через ![]() :
:
Заметим, что:
Получаем:
Откуда:
Осталось подставить в формулу для площади:
Доказано.
Пример
4. В треугольнике стороны равны![]()
Решение.
Зная три стороны и площадь треугольника, радиус описанной окружности можно найти из формулы:
А площадь, зная длины трех сторон, мы можем найти по формуле Герона:
Получаем:
Формула
площади треугольника через радиус вписанной окружности
Раз
есть формула, связывающая площадь треугольника и радиус описанной окружности,
должна быть и формула, связывающая площадь треугольника и радиус вписанной
окружности.
Мы доказали, что в любой треугольник можно вписать окружность. Если соединить центр этой окружности со всеми тремя вершинами, то исходный треугольник разобьется на три новых (мы уже доказывали, что эти три отрезка – части биссектрис соответствующих углов треугольника) (см. рис. 32).
 Рис.
32. Отрезки, которые соединяют центр вписанной в треугольник окружности с тремя
вершинами, – части биссектрис соответствующих углов треугольника
Рис.
32. Отрезки, которые соединяют центр вписанной в треугольник окружности с тремя
вершинами, – части биссектрис соответствующих углов треугольника
Во
всех этих трех малых треугольниках высоты равны радиусу вписанной окружности.
Применяя к каждому треугольнику формулу площади и складывая полученные выражения, имеем:
Получили новую формулу площади – произведение полупериметра на радиус вписанной окружности: Рис.
34. В четырехугольник вписана окружность, ее центр соединен отрезками с
четырьмя вершинами, а отрезки, в свою очередь, разбивают четырехугольник на
четыре малых треугольника, высоты которых равны радиусу вписанной окружности
Рис.
34. В четырехугольник вписана окружность, ее центр соединен отрезками с
четырьмя вершинами, а отрезки, в свою очередь, разбивают четырехугольник на
четыре малых треугольника, высоты которых равны радиусу вписанной окружностиВо-вторых, в отличие от формулы с радиусом описанной окружности, эту формулу нельзя назвать избыточной. Конечно, чаще всего, чтобы найти полупериметр, нужно знать длины всех сторон треугольника, но формально для применения этой формулы знать длины всех трех сторон треугольника необязательно – достаточно знать именно полупериметр.
Наконец, эту формулу чаще используют именно для нахождения радиуса вписанной окружности (в других формулах он у нас не фигурировал, поэтому для нас это будет единственный способ):
Например, зная три стороны треугольника и используя формулу Герона для нахождения площади, несложно найти радиус вписанной окружности по этой формуле.
Пример
5. В равнобедренном треугольнике основание равно![]()
![]() . Найти радиус вписанной окружности.
. Найти радиус вписанной окружности.
Решение.
Итак,
Радиус вписанной окружности практически всегда мы будем искать по формуле:
Осталось найти площадь. В общем случае можно было бы воспользоваться формулой Герона (можете попробовать решить эту задачу таким способом и убедиться, что получится такой же ответ). Мы же «схитрим» и воспользуемся тем, что треугольник равнобедренный и высота, проведенная к основанию, является также биссектрисой и медианой (см. рис. 36).
Поэтому несложно найти ее длину, используя теорему Пифагора:
Откуда:
Тогда площадь треугольника:
Получаем:Ответ: ![]() .
.
В завершение урока давайте посмотрим на все формулы сразу.
3 сентября 2021г
Решение задач.
№1.Найти
площадь криволинейной трапеции, изображенной на рисунке
Решение
№2. Вычислить
определенный интеграл:
Решение: Воспользуемся формулой
Ньютона-Лейбница.
Сначала находим первообразную
функцию F(x) . Далее подставляем значение верхнего предела в
первообразную функцию: F(b) .
Затем подставляем значение
нижнего предела в первообразную функцию: F(а).
Рассчитываем разность
F(b) - F(а), это и будет ответ.
№3. Найти
площадь криволинейной трапеции (х-1)2,
ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой
Ньютона-Лейбница.
Сначала находим первообразную
функцию F(x). Далее подставляем значение верхнего предела в первообразную
функцию: F(b) .
Затем подставляем значение
нижнего предела в первообразную функцию: F(а).
Рассчитываем разность
F(b) - F(а), это и будет ответ.
Задание 1:
Найти площадь криволинейной трапеции, ограниченной графиком
функции: f(x) = х2 и
прямыми у = 0, х = 1, х = 2.
Решение:
Начертим
график функции и прямые
Начнём со случаев, когда площадь фигуры
может быть вычислена по формуле (1).
Пример 1. Найти площадь фигуры, ограниченной графиком
функции 
,
осью абсцисс (Ox) и прямыми x = 1, x = 3.
Решение. Так как y = 1/x > 0 на отрезке [1; 3], то площадь криволинейной трапеции
находим по формуле (1):
Пример 2. Найти площадь фигуры, ограниченной графиком
функции ![]()
,
прямой x = 1 и осью абсцисс (Ox).
Решение. Результат применения формулы (1):
2 сентября 2021г
Тема: Вычисление определенного
интеграла. Нахождение площади плоской
фигуры.
На этом уроке будем учиться вычислять площади
плоских фигур, которые называются криволинейными трапециями.
Примеры таких фигур - на рисунке
С одной стороны, найти площадь плоской фигуры с
помощью определённого интеграла предельно просто. Речь идёт о площади фигуры,
которую сверху ограничивает некоторая кривая, снизу - ось абсцисс (Ox), а слева
и справа - некоторые прямые. Простота в том, что определённый интеграл функции,
которой задана кривая, и есть площадь такой фигуры (криволинейной
трапеции).
Но здесь нас подстерегают некоторые важные нюансы,
без понимания которых не решить большинство задач на это практическое
приложение определённого интеграла. Учтём эти нюансы и будем во всеоружии.
Для вычисления площади фигуры нам понадобятся:
Определённый интеграл от функции, задающей кривую,
которая ограничивает криволинейную трапецию сверху. И здесь возникает первый
существенный нюанс: криволинейная трапеция может быть ограничена кривой не
только сверху, но и снизу. Как действовать в этом случае? Просто, но это важно
запомнить: интеграл в этом случае берётся со знаком минус.
Пределы интегрирования a и b, которые
находим из уравнений прямых, ограничивающих фигуру слева и справа: x = a, x = b,
где a и b - числа.
Отдельно ещё о некоторых нюансах.
Кривая, которая ограничивает криволинейную трапецию
сверху (или снизу) должна быть графиком непрерывной и неотрицательной
функции y = f(x).
Значения "икса" должны принадлежать
отрезку [a, b]. То есть не учитываются такие, например, линии, как
разрез гриба, у которого ножка вполне вписывается в этот отрезок, а шляпка
намного шире.
Боковые отрезки могут вырождаться в точки. Если вы
увидели такую фигуру на чертеже, это не должно вас смущать, так как эта точка
всегда имеет своё значение на оси "иксов". А значит с пределами
интегрирования всё в порядке.
Теперь можно переходить к формулам и вычислениям.
2.Площадь фигуры, ограниченной графиками непрерывных
функций f(x),
3.Площадь фигуры, ограниченной графиками непрерывных
функций f (x) и
4.Площадь фигуры, ограниченной графиками непрерывных
функций f(x),
1 сентября 2021г
Тема: Применение определенного
интеграла для нахождения площади криволинейной трапеции.
Неопределенный интеграл от
функции
В неопределенном интеграле не заданы границы
интегрирования, и в результате нахождения неопределенного интеграла от
функции ![]()
Если заданы границы интегрирования, то мы
получаем определенный интеграл:
Здесь число ![]()
Для нас с точки зрения решения задач важное
значение имеет геометрический смысл определенного интеграла.
Рассмотрим фигуру, изображенную на рисунке:
Зеленая фигура, ограниченная сверху графиком
функции ![]() , слева прямой
, слева прямой![]() , справа прямой
, справа прямой![]() , и снизу осью ОХ называется криволинейной
трапецией.
, и снизу осью ОХ называется криволинейной
трапецией.
Геометрический смысл определенного
интеграла:
Определенный интеграл  - это число, равное площади криволинейной
трапеции - фигуры, ограниченой сверху графиком положительной на
отрезке
- это число, равное площади криволинейной
трапеции - фигуры, ограниченой сверху графиком положительной на
отрезке ![]() функции
функции ![]() , слева прямой
, слева прямой ![]() , справа прямой
, справа прямой![]() , и снизу осью ОХ.
, и снизу осью ОХ.
Пример 1.













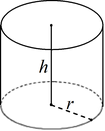
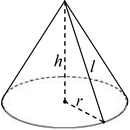
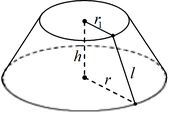

































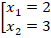



























































































































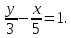



















































































Комментариев нет:
Отправить комментарий