Блог методиста ГБОУ СПО ЛНР "Комиссаровский колледж - агрофирма" Собко Натальи Анатольевны: 205

27 января 2022 г.

ПОВТОРЕНИЕ Тем: измерения в геометрии. Элементы комбинаторики. Элементы теории вероятностей. Элементы математической статистики.

20 января 2022 г.

ПОВТОРЕНИЕ.

13 января 2022 г.

ТЕМА: СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ. ПОВТОРЕНИЕ.

Теоремы сложения и умножения вероятностей, формулы

Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. $P(A+B) = P(A)+P(B)-P(AB)$ .
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае $P{AB)= P(A)\cdot P(B)$ .

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение $1\cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6$ , которое обозначается символом 6! и читается «шесть факториал».

В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов $P_n=1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6$ В нашем случае $n= 6$ .

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение $6 \cdot 5$ .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам

$A^{k}_{n}=n \cdot (n-1) \cdot (n-2) \dots \cdot(n-k+1)= \frac{n!}{(n-k)!}$

В нашем случае $n = 6, k = 2$ .

И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: $\frac {6 \cdot 5 \cdot 4}{1\cdot 2 \cdot 3} = 20$ . В общем случае ответ на этот вопрос дает формула для числа сочетаний из $n$ элементов по $k$ элементам:

$C^{k}_{n}=\frac{n \cdot (n-1) \cdot (n-2) \dots (n-k+1)}{1\cdot 2 \cdot 3 \dots \cdot k}=\frac{n!}{k! \cdot (n-k)!}.$

В нашем случае $n=6, k=3$ .

ТЕМА: СОБЫТИЯ, ВЕРОЯТНОСТЬ СОБЫТИЯ.

Теория вероятностей – это математическая наука, которая изучает закономерность в случайных событиях. К основным понятиям теории вероятностей относятся испытания и события.

Под испытанием (опытом) понимают реализацию данного комплекса условий, в результате которого непременно произойдет какое-либо событие. Например, бросание монеты - испытание; появление герба или цифры- событие.

Случайными называется событие, связанное с данным испытанием, которое при осуществлении испытания может произойти, а может и не произойти. Слово «случайное» для краткости часто опускают и говорят просто «событие». Например выстрел по цели - это опыт, случайные события в этом опыте- попадание в цель или промах.

Событие в данных условиях называются достоверным, если в результате опыта оно непременно должно произойти, и невозможным, если оно заведомо не произойдет. Например, выпадение не более шести очков при бросании одной игральной кости- достоверное событие; выпадение 7 очков при бросании одной игральной кости – невозможное событие.

События называются равновозможными, если ни одно из них не является объективно более возможным, чем другие. Например, при бросании монеты выпадение герба или числа- события равновозможные.

Говорят, что несколько событий в данном опыте образуют полную систему событий, если в результате опыта непременно должно произойти хотя бы одно из них. Например, при бросании игральной кости события, состоящие в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную систему событий. Пусть А- случайное событие, связанное с некоторым опытом. Повторим опыт п раз в одних и тех же условиях и пусть при этом событие А появилось т раз. Отношение 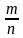называется частотой события А.

При многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу. Числовая мера степени объективной возможности события- это вероятность события. Вероятность события А обозначает Р(А).

Пусть из системы n несовместных равновозможных исходов испытания m исходов благоприятствуют событию A. Тогда вероятность события А называют отношение m числа исходов, благоприятствующих событию А к числу всех исходов данного испытания:P(A) = 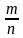. ЕслиА – случайное событие, то m 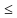n и P(A) 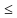1;

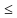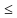Эта формула носит название классического определения вероятности. Если B- достоверное (или невозможное) событие, то m=n и P(B) = 1 (m = 0,P(B) = 0). Таким образом, вероятность события заключается в следующих пределах: 0 P (A) 1.

Независимость случайных событий. Событие B называют независимым от события A, если появление события A не изменит вероятности события В. Если событие В не зависит от события А, то и событие А не зависит от события В; это означает, что свойство независимости взаимно. Несколько событий называют попарно независимым, если каждые два события независимы.

Суммой А + В двух событий А+В называется событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А- попадание при первом выстреле, или в обоих выстрелах. Если события А и В несовместные, то А+В- событие, состоящее в появлении одного из этих событий, безразлично какого.

Теорема. Вероятность появления одного из двух несовместимых событий, безразлично какого, равна сумме вероятностей этих событий, безразлично какого, равна сумме вероятностей этих событий:

P(A+B) = P (A) + P (B).

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена.

Условной вероятностью РА(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна:

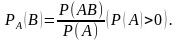
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило:

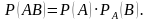
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна p, то вероятность того, что событие А появится в этих n испытаниях m раз, выражается формулой Бернулли Pn(m) = Cnk·pm·qn-m, где q = 1-p.

Число m0 называется наивероятнейшим числом наступлений события А в n испытаниях и равно целой части числа (n+1)p, а при целом (n+1)p наибольшее значение достигается при двух числах: m1=(n+1)p-1 и m2=(n+1)p.

Если р≠0 и р≠1, то число m0 можно определить из двойного неравенства

np-q ≤ m0 ≤ np+p.

Пример: В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

Решение.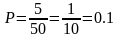

Пример: Участники жеребьёвки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого, наудачу извлечённого жетона, не содержит цифры 5.

Решение. Из чисел от 1 до 100 содержат число 5 девятнадцать чисел. Не содержит число пять – 81 число. Тогда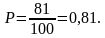

Пример: В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара (красного или синего).

Решение. Вероятность появления красного шара 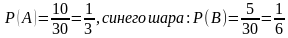События А и В несовместимы. Теорема сложения приемлема

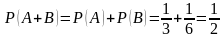
Пример: У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков конусный, а второй – эллиптический.

Решение. Вероятность того, что второй валик окажется эллиптическим, считая что первый валик – конусный, т.е. условная вероятность: 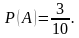Вероятность того, что второй валик окажется эллиптическим, считая что первый валик – конусный, т.е. условная вероятность: 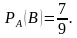По теореме умножения, искомая вероятность

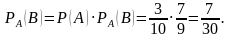
Пример: В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет
.
Вероятность события А при условии, что событие В не произошло, будет
.

Контрольная работа

ЗАДАНИЕ. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

ЗАДАНИЕ. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

ЗАДАНИЕ. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?

ЗАДАНИЕ. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?

11-13 января 2022 г.

Тема: Элементы комбинаторики. Решение уравнений.

Размещение элементов комбинаторики

Определение

Область математики, где изучается вопрос про количество разных соединений, которые подчинены тем или другим условиям, и которые можно составить из заданных элементов – это и есть комбинаторика. Размещение элементов – один из видов данной области.

Пусть даны три элемента $a, b, c$ . Из них можно создать такие соединения:

1) по одному элементу: $a, b, c$ ;

2) по два элемента: $ab, ac, bc,ba, ca, cb$ ;

3) по три элемента: $abc, acb, bac, bca, cab, cba$ .

Если, например, рассматривать соединения по два элемента, тогда некоторые из них отличаются элементами ( $ab$ и $ca$ ), другие – порядком элементов $(ac$ и $ca)$ . Такие соединения называются размещением из 3 элементов по 2.

Определение

Размещенными из $n$ элементов по $m$ называются такие соединения, в которых содержатся по $m$ элементов, взятых из данных $n$ элементов, и которые отличаются один от другого или элементами, или порядком элементов.

Число размещений обозначается $A_{n}^{m}$ . Из вышеописанного, мы видим, что $A_{3}^{1} = 3$ , $A_{3}^{2} = 6$ , $A_{3}^{3} = 6$ .

Число всех возможных размещений из $n$ элементов по $m$ равняется произведению $m$ последовательных натуральных чисел, из которых большее число $n$ , то есть:

$A_{n}^{m} = n(n - 1)(n - 2)...(n - (m - 1))$ .

(1)

Действительно, пусть нам дано $n$ элементов: $a, b, c, ..., k, l$ .

Рассмотрим размещение по одному элементу. Понятно, что их будет $n$ , то есть $A_{n}^{1} = n$ .

Теперь рассмотрим, какие возможные размещения по 2 элемента. Чтобы их получить, мы допишем к каждому из $n$ данных элементов ещё по одному, которые брались из остальных $(n - 1)$ элементов. Так, к элементу $a$ допишем последовательно остальные элементы: $b, c, ..., k, l$ ; к элементу $b$ последовательно остальные элементы: $a, c, ..., k, l$ и т. д.

Получим все размещения из $n$ элементов по 2:

$\left\{ \begin{aligned} ab, ac, ad, ..., ak, al - (n - 1);\\ ba, bc, bd, ..., bk, bl - (n - 1);\\ ca, cb, cd, ..., ck, cl - (n - 1);\\ - - - - - - - - - - - - \\ la, lb, lc, ..., lk - (n - 1) \end{aligned} \right$

Записано $n$ строк, а число всех размещений в каждом из этих строк $(n - 1)$ . Общее количество всех размещений равняется произведению $n$ на $(n - 1)$ , то есть:

$A_{n}^{2} = n(n - 1)$ .

Чтобы получить рзмещение по 3 элемента в каждом, нам нужно к каждой из записанных пар элементов приобщить ещё по одному элементу из $(n - 2)$ элементов, что остались.

Например, к $ab$ необходимо приобщить один из $(n - 2) - x$ элементов $c, d, ..., k, l$ . Тогда всех размещений по 3 элемента будет:

$A_{n}^{3} = n(n - 1)(n - 2)$ и т. д.

Иногда встречаются задачи на размещение с повторениями.

Определение

Размещение из $n$ элементов по $m$ с повторениями называются такие соединения, которые содержат по $m$ элементов, взятых из данных $n$ элементов, причём отдельные элементы могут появляться $0, 1, 2, ...$ , $m$ раз.

Число размещений с повторениями обозначаются через $\overline{A}_{n}^{m}$ и вычисляются по формуле:

$\overline{A}_{n}^{m} = n^{m}$ .

Перестановка элементов комбинаторики

Определение

Перестановка элементов – это размещение из $n$ элементов по $n$ и обозначаются $P_{n}$ .

Согласно с определением:

$P_{n} = A_{n}^{n} = n(n - 1)(n - 2)...(n - (n - 1)) = n(n - 1)(n - 2)...1$ .

Произведение всех натуральных чисел от $1$ до $n$ обозначается $n!$ , а читается ( $n$ факториал).

Таким образом,

$n! = 1 * 2 * 3...(n - 1)n = (n - 1)!n$ .

Тогда формула для вычисления количества перестановок запишется:

$P_{n} = n!$

(3)

При этом имеется ввиду, что $1! = 1$ .

Обратите внимание!

Иногда встречается обозначение $0!$ . Принято считать, что $0! = 1$ .

Комбинации или сочетание элементов комбинаторики

Определение

Сочетание элементов (комбинации) из $n$ элементов по $m$ (обозначается $C_{n}^{m}$ ) называется то размещение из $n$ элементов по $m$ , которые отличаются хотя бы одним элементом.

Число комбинаций вычисляется по формуле:

${C_{n}^{m}} = {A_{n}^{m}\over{P_{m}}} = {n(n - 1)(n - 2)...(n - (m - 1))\over{1 * 2 * 3 ... * m}}$

(4)

Формулу (4) объясним на таком примере:

Пусть даны 4 элемента $a, b, c, d$ , комбинациями из этих элементов по будут:

$abc, abd,acd, bcd$ .

Порядок элементов в комбинации роли не играет. Если в каждой из этих комбинаций сделать всевозможные перестановки, тогда у нас получатся всевозможные размещения из 3 элементов:

$\begin{vmatrix} abc\quad{abd}\quad{acd}\quad{bcd}\\ acb\quad{adb}\quad{adc}\quad{bdc}\\ bac\quad{bda}\quad{cad}\quad{cbd}\\ bca\quad{bad}\quad{cda}\quad{cdb}\\ cab\quad{dab}\quad{dac}\quad{dbc}\\ cba\quad{dba}\quad{dca}\quad{dcb}. \end{vmatrix} \right$

Число таких размещений равняется $6 * 4 = 24$ .

Таким образом, число всех размещений из $n$ элементов по $m$ равняется числу всех возможных сочетаний элементов по $m$ , умноженному на число всех перестановок, которые можно сделать из $m$ элементов, то есть:

$A_{n}^{m} = C_{n}^{m} * P_{m}$ ,

откуда получается формула (4).

Посмотрите пример:

$C_{4}^{3} = {4 * 3 * 2\over{1 * 2 * 3}} = 4$ .

Умножим числитель и знаменатель в формуле (4) на $1 * 2 * 3 * ... * (n - m) = (n - m)!$ . Тогда получим:

${C_{n}^{m}} = {n(n - 1)...(n - (m - 1))\over{1 * 2 * 3...m}} * {(n - m)...3 * 2 * 1\over{(n - m)...3 * 2 * 1}}$

В итоге получаем:

${C_{n}^{m}} = {n!\over{(n - m)!m!$

(5)

По определению принимают $C_{n}^{0} = 1$ . Это определение можно получить из формулы (5), если принять во внимание, что $0! = 1$ .

При вычислении числа комбинаций иногда удобно пользоваться соотношением:

$C_{n}^{m} = C_{n}^{n - m}$

(6)

Действительно, если по формуле (5) записать $C_{m}^{n - m}$ , тогда получим:

${C_{n}^{n - m}} = {n!\over{(n - (n - m))!(n - m)!}} = {n!\over{{m!(n - m)!$

(7)

Последнее выражение совпадает с правой частью в формуле (5).

Отметим ещё, что числа $C_{n}^{0}, C_{n}^{1}, C_{n}^{2}, ..., C_{n}^{n - 2}, C_{n}^{n - 1}, C_{n}^{n}$ – это коэффициенты в биноме Ньютона:

$(a + b)^{n} = C_{n}^{0}a^{n}b^{0} + C_{n}^{1}a^{n - 1}b^{1} + C_{n}^{2}a^{n - 2}b^{2}+...+\\ + C_{n}^{n - 2}a^{2}b^{n - 2} + C_{n}^{n - 1}ab^{n - 1} + C_{n}^{n}a^{0}b^{n}$

(8)

причём согласно с равенством (6) коэффициенты, равноотдалённые от окончания в формуле (8), равные между собой, то есть:

${C_{n}^{0}} = {C_{n}^{n} = 1}$ , ${C_{n}^{1}} = {C_{n}^{n - 1}} = {n}$ , ${C_{n}^{2}} = {C_{n}^{n - 2}} = {n(n - 1)\over{1 * 2}}$ и т. д.

Перестановки и комбинации с повторениями

Иногда бывают перестановки с повторениями: $P_{n}(m_{1}, m_{2}, ..., m_{k})$ , которые можно образовать из $n$ элементов, среди которых $m_{1}$ одинаковых элементов 1-го типа, $m_{2}$ одинаковых элементов 2-го типа, и т. д. $m_{k}$ одинаковых элементов к-го типа, причём $m_{1} + m_{2} + ... + m_{k} = n$ находятся по формуле:

$P_{n}(m_{1}, m_{2}, ..., m_{k}) = {n!\over{m_{1}! * m_{2}! * ... * m_{k}!}$

(9)

Теперь рассмотрим комбинации с повторениями.

Число комбинаций с повторениями (обозначается $\overline{C}_{n}^{m}$ ) из $n$ по $m$ элементов есть такие соединения по $m$ элементов в каждой (элементы могут повторяться), которые выбираются из элементов $n$ типов, причём порядок элементов не учитывается, и находится по формуле:

$\overline{C}_{n}^{m} = C_{n + m - 1}^{m}$

(10)

где может быть $m > n$ .

Примеры решения задач с элементами комбинаторики

Пример 1

Задача

Студенты группы изучают 9 дисциплин по 3 пары ежедневно. Сколько существует способов, чтобы распределить пары на один день?

Решение

Все возможные способы распределения пар на день представляют собой, очевидно, все возможные размещения из 9 элементов по 3. Поэтому их количество равняется:

$A_{9}^{3} = 9 * 8 * 7 = 504$ .

Ответ

Существует 504 размещений.

Пример 2

Задача

Автомобильный номер состоит из 5 цифр (из такого набора: $(0, 1, 2, 3, ..., 9)$ и двух букв. В соединении из букв для номеров автомобилей, какие зарегистрированы в Московской области, на первом месте стоит буква $A$ , а на втором месте одна из букв А, Б. В, И. К, Н. Сколько автомобильных номеров можно составить в области?

Решение

Числовая часть номера – один из размещений из $n = 10$ по $m = 5$ с повторениями. И количество:

$\overline{A}_{10}^{5} = 10^5$

Из них необходимо исключить размещение 000-00, так как такой номер не используется, то есть, всех числовых соединений будет:

$10^5 - 1 = 99 999$ .

Количество соединения букв 7. Первая буква фиксированная, тогда остаётся шесть. Общее число всех автомобильных номеров при изложенной системе равняется:

$(10^{5} - 1) * 6 = 599994$ .

Ответ

Автомобильных номеров в одной области можно составить по числам – 99 999, а по буквам – 599994.

Пример 3

Задача

Сколько пятизначных телефонных номеров можно составить используя цифры 3, 4, 5, 6, 7 (без повторений)?

Решение

Так как каждый номер телефона складывается из 5 цифр, тогда такие номера будут отличаться только порядком цифр, то есть это будут перестановки, и их количество равняется:

$P_{5} = 5! = 1 * 2 * 3 * 4 * 5 = 120$ .

Ответ

Всего можно составить 120 пятизначных номеров.

Пример 4

Задача

Сколько есть способов, чтобы заполнить карточку спортлото, в которой из 49 чисел необходимо выбрать 6?

Решение

Две заполненные карточки считаются разными, если среди выбранных 6 чисел они отличаются хотя бы одним числом, то есть это будут комбинации, и их количество равняется:

${C_{49}^{6}} = {49 * 48 * 47 * 46 * 45 * 44\over{1 * 2 * 3 * 4 * 5 * 6}} = 13 983 816$ .

Ответ

Количество комбинаций = $13 983 816.$

Пример 5

Задача

Сколько есть способов, чтобы в данном тайме тренер смог бы выставить на поле 5 баскетболистов, если в команде 10 игроков, причём одного из ведущих игроков тренер планирует задействовать в игре не заменяя на другого игрока весь тайм?

Решение

Так как один из ведущих игроков должен находится на поле в игре весь тайм, тогда менять придётся только 4 игрока из оставшихся 9, то есть у нас получается:

${C_{9}^{4}} = {9 * 8 * 7 * 6\over{1 * 2 * 3 * 4}} = 126.$

Ответ

Есть 126 способов.

Пример 6

Задача

Сколько есть способов, чтобы расставить на первой горизонтальной шахматной доски такие фигуры: две ладьи, два коня, два слона, одного ферзя и одного короля?

Решение

Всего 8 фигур, причём $m_{1} = 2$ , $m_{2} = 2$ , $m_{3} = 2$ , $m_{4} = 1$ , $m_{5} = 1$ , тогда:

${P_{5}} = {(2, 2, 2, 1, 1)} = {8!\over{(2!)}^{3}(1!)^{3}} = 5 040$ .

Ответ

На первой горизонтальной шахматной доске с перестановками фигур можно расставить 5 040 раз.

Пример 7

Задача

Сколько разных соединений букв можно образовать, переставляя эти буквы:

1. В слове “мама”;

2. в слове параллелограмм.

Записать соединения букв.

Решение

1. В слове “мама” $n = 4$ буквы, при этом две буквы “м”, и две буквы “а”. По формуле (9) всех перестановок будет:

${P_{4}(2, 2)} = {4!\over{2!2!}} = {4 * 3 * 2 * 1\over{2 * 2}} = 6$ .

А сами перестановки будут такими: “мама”, “маам”, амам”, “аамм”, “амма”.

2. В слове “параллелограмм” 12 букв, из них букв “а” – 3, “г” – 1, “е” – 1, “л” – 2, “м” – 1, “о” – 1, “п” – 1, “р” – 2. Всех перестановок будет:

${P_{12}(3, 1, 1, 2, 1, 1, 1, 2)} = {12!\over{3!(2!)^{2}(1)^{5}}} = 19 958 400$ .

Ответ

Всевозможных перестановок будет – $19958400$ .

Пример 8

Задача

На складе нужно получить 5 однотипных деталей, каждая из которых может быть покрашена в один из трёх цветов: красный, чёрный, зелёный. Сколько имеется способов, чтобы выбрать 5 деталей трёх цветов?

Решение

$\overline{{C}_{3}^{5}} = {C_{3 + 5 - 1}^{5}} = {C_{7}^{5}} = {C_{7}^2}} = {7 * 6\over{1 * 2}} = 21$ .

Ответ

Для того, чтобы выбрать 5 деталей 3 цветов, мы нашли 21 способ.

10 января 2022 г.

Тема: Формула Бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.

1. Бином Ньютона - название формулы, выражающей степень двучлена в виде суммы одночленов.

Формулу для квадрата двучлена

(а + b)² = = а² + 2ab + b²

знали, еще математики Древнего Вавилона, а древнегреческие математики знали ее геометрическое истолкование.

Если умножить обе части этой формулы на (а + b) и раскрыть скобки, то получим:

(а + b)³ = (а² + 2ab + b²)(а + b) = а³ + a²b + 2a²b + 2ab² + ab² + b³,

т. е. (а + b)³ = a³ + 3a²b + 3ab² + b³.

Аналогичный шаг может привести к следующей формуле:

(а + b)⁴ = а⁴ + 4а³b + 6 a²b² + 4ab³ + b⁴ .

Легко заметить закон образования коэффициентов: коэффициент 4 при a³b есть сумма коэффициентов 3 и 1 при a²b и а³. Аналогично, коэффициент 6 при a²b² является суммой (3 + 3) коэффициентов при ab² и a²b. По тому же закону получаем и коэффициент 4 при ab³.

Таким образом, коэффициент С^kn при аⁿ^-^k b^kв разложении (а + b)ⁿ равен сумме коэффициентов C^k^-1n-1и C^kn-1при аⁿ^-^k b^k^-1и при аⁿ^-^k^-1 b^kразложении

(а + b)ⁿ^-1, а коэффициенты при аⁿ и при bⁿ равны единице.

Отсюда следует, что коэффициенты С^kn в равенстве:

(а + b)ⁿ = аⁿ + С¹n аⁿ^-1b + ... + С^kn а^n-kb^k + ... + bⁿ (1)

являются членами (n+1)-й строки треугольника Паскаля.

Это утверждение было известно задолго до Паскаля - его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло).

2. Биномиальные коэффициенты.

Первое дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел С^kn (биномиальных коэффициентов) до п = 12 включительно.

Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Блез Паскаль в 1654 г. Еще до этого было известно, что числа

являются в то же время числами «сочетаний без повторений» из n элементов по k.

В 1664-1665 гг. И. Ньютон установил, что формула (1) обобщается на случай произвольных (дробных и отрицательных) показателей, но при этом получается сумма из бесконечного множества слагаемых. Именно он показал, что при | х | < 1

(2)

При п = — 1 формула (2) превращается в известную формулу для суммы бесконечной геометрической прогрессии:

Треугольник Паскаля.

На рис. 1 изображено несколько первых строк числового треугольника, образованного по следующему правилу: по краям каждой строки стоят единицы, а каждое из остальных чисел равно сумме двух стоящих над ним чисел предыдущей строки.

По этому правилу легко выписывать одну за другой новые строки этого треугольника. Именно в такой форме он приведен в «Трактате об арифметическом треугольнике» французского математика Б. Паскаля (1623-1662), опубликованном в 1665 г., уже после смерти автора.

Популярность чисел, составляющих треугольник Паскаля, не удивительна: они возникают в самых естественных задачах алгебры, комбинаторики, теории вероятностей, математического анализа, теории чисел.

Сколько различных k-элементных множеств (сочетаний) можно образовать из данных п элементов?

Каковы коэффициенты многочлена (1 +х)ⁿ?

Сколько существует строчек из п единиц и нулей, в которых ровно k единиц?

Сколькими разными путями можно спуститься из верхней точки А на рис 2. в k-й перекресток n-го ряда?

Рис 2

На все эти вопросы ответ дают числа С^kn , треугольника Паскаля. Обозначение С^kn предполагает, что верхняя строка треугольника Паскаля состоит из одного числа С⁰0 = 1, следующая (первая)-из двух чисел С⁰1 = С¹1 =1, и вообще п-я строка состоит из п+1 чисел:

Числа С^kn называют обычно числами сочетаний из п элементов по k, или биномиальными коэффициентами в некоторых книгах для них используют обозначение . Оно удобно для запоминания простой формулы, позволяющей по заданным номерам n и k сразу вычислить, какое число стоит на к-м месте в n-й строке треугольника Паскаля:

Используя обозначение факториала т! = = 1 • 2 •... • m, эту формулу можно записать еще короче:

В «равнобедренной» форме треугольника Паскаля на рис. 1 очевидно свойство симметрии каждой строки С^kn = Сⁿ^-^kn ; при этом посередине строки стоит самое большое число (если п четно) или два самых больших числа (если п нечетно), а к краям числа монотонно убывают.

Если записать тот же треугольник в «прямоугольной» форме (рис.3), то целый ряд свойств треугольника Паскаля, связанный с суммами его чисел, будет удобнее наблюдать. В частности, сумма нескольких первых чисел каждого столбца равна идущему за ними числу следующего столбца:

Рис.3

Числа называются треугольными числами, а числа
- пирамидальными;

а при т> к,

Суммы чисел по «восходящим» (зеленым) диагоналям на рисунке 3 равны последовательным числам Фибоначчи.

Для применений в теории вероятностей особенно важны асимптотические формулы для чисел треугольника Паскаля, т.е. приближенные оценки этих чисел при больших п.

Уважаемые студенты! До 8 октября предоставить конспекты, можно в сканированном виде на почту и контрольную работу!

04 октября 2021 г.

Тема: Формулы объема шара и площади сферы.

Шар – это совокупность всех точек пространства, находящихся от данной точки на расстоянии, не больше данного. Причём, данная точка называется центром шара, а данное расстояние – радиусом шара.

Радиусом шара называют всякий отрезок, соединяющий центр шара с любой точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.

Отрезок, соединяющий две точки шаровой поверхности и не являющийся диаметром шара, т.е. не проходящий через центр шара, называется хордой шара.

Понятно, что сечение шара плоскостью есть круг.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом шара.

Итак, справедлива следующая теорема: объём шара радиуса равен .

Докажем теорему. Пусть нам дан шар радиуса с центром в точке. Выберем ось так, чтобы начало оси совпадало с центром шара.

Тогда отрезок это есть радиус шара
Докажем, что объём шара равен .

На оси отметим произвольную точку и рассмотрим сечение шара плоскостью проходящее через эту точку перпендикулярно к оси . Заметим, что такое сечение шара плоскостью является кругом с центром в точке .

Отрезок .

Обозначим радиус этого круга через , а его площадь через , где –абсцисса точки .

Выразим площадь через и радиус шара .

Из прямоугольного треугольника по теореме Пифагора найдём радиус круга. Тогда имеем.

Площадь круга . Заменим радиус круга выражением . Тогда получаем, что .

Заметим, что эта формула верна для любого положения точки на диаметре . Иначе говоря, верна для всех , удовлетворяющих условию .

Так как мы с вами выразили площадь через , то можем вычислить объём шара с помощью основной формулы объёма тела. Вспомним её: объем тела равен .

Итак, применяя основную формулу для вычисления объёмов тел получаем, что объём шара равен

Этим мы с вами доказали, что объём шара с радиусом равным можно вычислить по формуле .

Что и требовалось доказать.

Ранее мы с вами без доказательства привели формулу для вычисления площади сферы. Напомню, что площадь сферы можно вычислить по формуле: .

Теперь давайте выведем эту формулу, пользуясь формулой объёма шара.

Итак, рассмотрим сферу радиуса с центром в точке О и описанный около неё многогранник, имеющий граней.

Напомним, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

Занумеруем грани в произвольном порядке и обозначим через – площадь -й грани.

Затем соединим центр О сферы отрезками со всеми вершинами многогранника. При этом получим эн пирамид с общей вершиной О, основаниями которых являются грани многогранника, а высотами – радиусы сферы, проведенные в точки касания граней многогранника со сферой.

Следовательно, объём -й пирамиды равен , а объём всего описанного многогранника равен:

. Где

– площадь поверхности многогранника.

Отсюда получаем: .

Теперь будем неограниченно увеличивать таким образом, чтобы наибольший размер каждой грани описанного многогранника стремился к нулю. При этом объём описанного многогранника будет стремиться к объёму шара. В самом деле, если наибольший размер каждой грани описанного многогранника не превосходит , то описанный многогранник содержится в шаре радиуса с центром в точке .

Но ведь с другой стороны, описанный многогранник содержит исходный шар радиуса . Значит, объём .

Так как выражение при , то и объем при ().

Переходя затем к пределу, получаем, что

По определению площади сферы , следовательно, .

Что и требовалось доказать.

Задача: объём шара равен см3. Найдите диаметр шара.

Решение: запишем формулу для вычисления объёма шара.

По условию задачи объём шара равен см3.

Отсюда видим, что радиус шара равен

(см). Напомним, что диаметр шара вдвое больше его радиуса. Тогда диаметр нашего шара равен

(см).

Запишем ответ.

Задача: радиус шара увеличили в раза. Во сколько раз увеличился объём шара?

Решение: запишем формулу для вычисления объёма шара.

Так как по условию задачи радиус исходного шара увеличили в 2 раза, то радиус данного шара будет равен . Подставляя данный радиус в формулу для вычисления объёма шара

видим, что объём исходного шара увеличился в 8 раз. Следовательно, ответ: объём шара увеличился в 8 раз.

Задача: в цилиндр вписан шар. Найдите отношение объёма шара к объёму цилиндра.

Решение: шар, вписанный в цилиндр, касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга, параллельной основаниям цилиндра. Отсюда следует, что , а высота цилиндра равна .

Объём шара вычисляется по формуле

, а объём данного цилиндра можно вычислить по формуле

, где

– это площадь основания,

- высота цилиндра. Так как высота данного цилиндра равна двум радиусам, а площадь основания равна

, то объём цилиндра равен

Найдём отношение объёма шара к объёму цилиндра. Получаем, что объём шара относится к объёму цилиндра, как .

1 октября 2021г

Тема: Площадь поверхности и объем конуса. Решение задач.

конус – это тело, полученное при вращении прямоугольного треугольника вокруг прямой, проходящей через один из его катетов.

Назовём элементы конуса.

Осью конуса называется прямая вращения.

Основание конуса – круг радиуса , который равен катету треугольника вращения.

Радиус конуса – это радиус его основания.

Вершина конуса – неподвижная вершина треугольника вращения.

Образующая конуса – отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все образующие конуса равны между собой.

Высота конуса – перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота конуса совпадает с неподвижным катетом треугольника вращения.

В конусе радиус основания , высота и образующая связаны следующим соотношением:.

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса.

Осевым сечением конуса называется сечение конуса плоскостью, проходящей через его ось.

Осевое сечение конуса – равнобедренный треугольник, боковые стороны которого – образующие, а основание – диаметр основания конуса.

Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой боковой поверхности конуса является круговой сектор.

Обратите внимание, радиус сектора равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

Площадь боковой поверхности конуса можно вычислить по следующим формулам:

где – длина окружности основания, – радиус основания,

– образующая.

Площадь полной поверхности конуса равна сумме площади боковой поверхности конуса и площади его основания.

Тогда площадь полной поверхности конуса можно вычислить по формуле^

,где

– радиус основания конуса,

– его образующая.

Объём конуса равен одной третьей произведения площади основания на высоту.

Тогда его можно вычислить по формуле:,

где – радиус основания конуса, – его высота.

Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая (нижняя) называется усечённым конусом.

Усечённым конусом называется часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. Усечённый конус имеет ось, высоту , радиусы оснований и ,

образующую . Осевое сечение усечённого конуса – равнобедренная трапеция.

Площадь боковой поверхности усечённого конуса и объём усечённого конуса равен разности площадей боковых поверхностей и объёмов полного конуса и отсечённого.

Площадь боковой поверхности усечённого конуса можно найти по следующим формулам:

Объём усечённого конуса можно вычислить по следующим формулам:

где и – площади оснований, – высота усечённого конуса;

или ,

где – высота усечённого конуса, и – радиусы верхнего и нижнего оснований.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Радиус основания конуса равен 3 см, высота конуса равна 4 см. Найдите площадь боковой поверхности и объём конуса.

Решение.

Задача вторая. В конус вписана правильная треугольная пирамида с площадью основания см² и углом наклона бокового ребра к основанию, равным

. Найдите объём и площадь полной поверхности конуса.

Решение.

Задача третья. В равносторонний конус с радиусом основания, равным 4 см, вписан прямоугольный параллелепипед в основании которого лежит квадрат, с высотой см так, что одно его основание принадлежит основанию конуса, а вершины другого основания принадлежат боковой поверхности конуса. Найдите объём параллелепипеда. В ответе запишите значение .

Решение.

Задача четвёртая. Длины радиусов оснований и образующей усечённого конуса равны соответственно 7 см, 15 см и 17 см. Вычислите его высоту.

Решение.

Тема: Площадь поверхности и объем цилиндра. Решение задач.

цилиндр – это тело, полученное при вращении прямоугольника вокруг прямой, проходящей через одну из его сторон.

Назовём элементы цилиндра.

Основания цилиндра – два равных круга радиуса .

Отрезок, соединяющий окружности оснований и перпендикулярный основаниям, называется образующей цилиндра и обозначается . Все образующие цилиндра параллельны и равны.

Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Высота цилиндра – перпендикуляр, опущенный из любой точки одного основания на другое, или другими словами, это расстояние между плоскостями оснований цилиндра. Образующая цилиндра равна его высоте.

Радиусом цилиндра называется радиус его основания.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.

Сечение, параллельное оси цилиндра, является прямоугольником.

Сечение, перпендикулярное оси цилиндра, является кругом, равным основаниям цилиндра.

Боковая поверхность цилиндра может быть развёрнута в прямоугольник со сторонами, одна из которых равна длине окружности основания, другая – высоте цилиндра.

Площадь боковой поверхности цилиндра можно вычислить по следующим формулам:

где – длина окружности основания, – высота цилиндра,

– радиус основания,

– образующая.

Площадь полной поверхности цилиндра равна сумме площади боковой поверхности цилиндра и двух площадей его оснований.

Тогда площадь полной поверхности цилиндра можно вычислить по формуле:

где – радиус оснований цилиндра, – его высота.

Объём цилиндра равен произведению площади основания на высоту.

Тогда его можно вычислить по формуле:

где – радиус оснований цилиндра, – его высота.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Радиус основания цилиндра равен 4 см, высота цилиндра равна диаметру его основания. Найдите площадь боковой поверхности цилиндра.

Решение.

Задача вторая. Найдите площадь сечения цилиндра плоскостью, параллельной его оси и проходящей на расстоянии 4 см от неё, если площадь полной поверхности цилиндра равна см2, а площадь боковой поверхности см2.

Решение.

Задача третья. Призма со сторонами основания 3 см и 4 см и диагональю 13 см вписана в цилиндр. Найдите объём и площадь полной поверхности цилиндра.

Решение.

Задача четвёртая. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу . Диагональ полученного сечения равна и удалена от оси цилиндра на расстояние . Найдите объём цилиндра.

Решение.

Задача пятая. В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Найдите, чему равен объём детали. Ответ выразите в см3.

Решение.

24 сентября 2021г

Тема: Площадь поверхности и объем пирамиды. Решение задач.

пирамида – это многогранник, в основании которого лежит –угольник, а остальные граней – треугольники с общей вершиной.

Многоугольник называется основанием пирамиды.

Треугольники , , …, называются боковыми гранями пирамиды.

Точка – вершиной пирамиды, а отрезки , , …,

– её боковыми рёбрами.

Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.

Пирамиду с вершиной и основанием называют

-угольной пирамидой и обозначают так:

Диагональное сечение – это сечение пирамиды плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды.

Тогда площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех её граней.

Объём пирамиды равен:

Пирамида, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.

Пирамида называется правильной, если её основанием является правильный многоугольник, а все боковые рёбра равны.

Отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.

Высота боковой грани правильной пирамиды, проведённая из её вершины к ребру основания, называется апофемой.

Выше изображена правильная пирамида. – одна из её апофем. Все апофемы правильной пирамиды равны друг другу.

Отметим некоторые свойства правильной -угольной пирамиды.

1. В правильной -угольной пирамиде все боковые рёбра равны между собой.

2. Боковые рёбра равно наклонены к основанию.

3. Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.

4. Боковые грани равно наклонены к основанию.

5. Вершина проектируется в центр основания (основание высоты совпадает с центром основания).

6. Площадь боковой поверхности правильной пирамиды равна:

7. Объём правильной четырёхугольной пирамиды со стороной основания

и высотой равен:

Параллельное сечение пирамиды – сечение пирамиды плоскостью, параллельной основанию.

Параллельное сечение пирамиды обладает следующими свойствами:

1. сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки;

2. в сечении получается многоугольник, подобный основанию;

3. площади сечения и основания относятся как квадраты их расстояний до вершины.

Усечённая пирамида – это часть пирамиды, заключённая между основанием и параллельным сечением пирамиды.

Основания усечённой пирамиды – подобные многоугольники, лежащие в параллельных плоскостях.

Боковые грани усечённой пирамиды – трапеции.

Высота усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего.

Площадь полной поверхности усечённой пирамиды равна сумме площади боковой поверхности и площадей двух оснований.

Объём усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его ещё можно вычислить по следующей формуле:.

Правильная усечённая пирамида получается из правильной пирамиды.

Апофема – высота боковой грани правильной усечённой пирамиды.

Площадь боковой поверхности правильной усечённой пирамиды равна:

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. Дана треугольная пирамида, боковые рёбра которой взаимно перпендикулярны и равны см, см и см. Найдите площадь боковой поверхности пирамиды.

Решение.

Задача вторая. Дана правильная четырёхугольная пирамида со стороной основания

см и высотой

см. Найдите площадь полной поверхности пирамиды.

Решение.

Задача третья. Найдите высоту правильной усечённой треугольной пирамиды

, если стороны её оснований равны

см и

см, а боковое ребро равно

см.

Решение.

Задача четвёртая. В пирамидебоковое ребро перпендикулярно основанию и равно ребру . Треугольник – прямоугольный с катетами см и см. Найдите объём пирамиды.

Решение.

Задача пятая. Найдите объём правильной треугольной пирамиды с ребром основания, равным

см, и боковым ребром, равным

см.

Решение.

17 сентября 2021г

Тема: Площадь поверхности и объем призмы. Решение задач.

Напомним, что призмой называется многогранник, у которого две грани – равные

-угольники, лежащие в параллельных плоскостях (эти грани называются основаниями призмы), а остальные

граней – параллелограммы.

Эти параллелограммы называются боковыми гранями, а их стороны, не лежащие на основаниях призмы, называются боковыми рёбрами призмы.

Боковые рёбра призмы параллельны и равны.

Высотой призмы называется расстояние между основаниями.

Площадью боковой поверхности призмы называется сумма площадей её боковых граней.

Площадью полной поверхности призмы – сумма площадей её боковых граней и двух площадей оснований.

Объём призмы равен произведению площади основания на высоту.

Призма, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.

Рассмотрим наклонную призму. Здесь основания – равные многоугольники, лежащие в параллельных плоскостях. Боковые грани – параллелограммы. Высота призмы – перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего. Боковые рёбра призмы равны и параллельны. Диагональ призмы соединяет две вершины, не лежащие в одной грани. Диагональное сечение проходит через два боковых ребра, не лежащих в одной грани, и является параллелограммом. Площадь боковой поверхности призмы равна сумме площадей боковых граней. Площадь полной поверхности равна сумме площади боковой поверхности и двух площадей оснований.

Рассмотрим прямую призму. Здесь боковые рёбра перпендикулярны основаниям. Боковые грани – прямоугольники. Высота равна боковому ребру. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту (на боковое ребро).

И рассмотрим ещё правильную призму. Здесь в основании лежит правильный многоугольник. Боковые рёбра перпендикулярны основанию. Боковые грани – равные прямоугольники.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. В основании прямой четырёхугольной призмы лежит четырёхугольник со сторонами см,см,см и см. Высота призмы равна см. Найдите площадь боковой поверхности призмы.

Решение.

Задача вторая. Дана шестиугольная наклонная призма с боковым ребром

см. Периметр сечения призмы плоскостью, перпендикулярной боковому ребру, равен

см. Найдите площадь боковой поверхности призмы.

Решение.

Задача третья. Дана прямая пятиугольная призма, в основание которой вписана окружность с радиусом см. Площадь основания призмы равна см2, боковое ребро призмы равно см. Найдите площадь боковой поверхности призмы.

Решение.

Задача четвёртая. Дана прямая четырёхугольная призма
В основании призмы лежит прямоугольная трапеция с основаниями
см, см и , в которую можно вписать окружность. Диагональное сечение призмы является квадратом. Найдите площадь полной поверхности призмы.

Решение.

10 сентября 2021г

Тема: Понятие об объеме тела. Отношение объемов подобных тел. Формулы объема куба, параллелепипеда, призмы.

Объем

Объем - это величина, показывающая какое количество пространства занимает тело. Например, объем куба, ребро которого равно единице, равен единице. Объем измеряется в кубических единицах. В каких единицах измерения исчисляются три измерения тела (длина, ширина, высота), в таких единицах измеряется и объем. Например, если ребро куба равно 1 м, то его объем будет равен одному кубическому метру, т.е. 1 м3. Объем прямоугольного параллелепипеда

Пусть даны два прямоугольных параллелепипеда ABCDA'B'C'D' и ABCDEE'E"E"' с общим основанием ABCD и высотами АЕ и АA' (Рис.1). Обозначим объем параллелепипеда ABCDA'B'C'D' - V, а объем параллелепипеда ABCDEE'E"E"' - V1.

Рис. 1 Объем прямоугольного параллелепипеда.

Разобьем сторону AA' на большое число n равных частей. Т.е. каждая часть параллелепипеда имеет высоту, равную АA'/ n. Пусть m - число частей, которые укладываются на ребре АЕ.

Возьмем куб объемом одна единица и три прямоугольных параллелепипеда с измерениями: a:1:1, a:b:1, a:b:c (Рис.1.1). Обозначим их объемы как V1, V2, V. Тогда можно составить следующие соотношения:

Рис. 1.1 Объем прямоугольного параллелепипеда V = abc.

Перемножив эти три равенства почленно, получим, что объем прямоугольного параллелепипеда равен: V = abc

Объем призмы

Пусть дана треугольная призма ABCA'B'C' (Рис.3).

Достроим данную призму до параллелепипеда. Тогда точка пересечения диагоналей (точка О) параллелограмма BB'C'C будет являться точкой симметрии. Следовательно объем призмы будет равен половине объема параллелепипеда.

Так как объем параллелепипеда равен произведению площади основания на высоту, то объем призмы будет равен также произведению площади основания на высоту.

Допустим, что основание призмы есть многоугольник. Тогда его можно разбить на несколько треугольников. Следовательно вся призма будет представлять собой несколько треугольных призм. А общий объем будет равен сумме объемов этих призм.

Таким образом: объем любой призмы равен произведению площади ее основания на высоту.

Объем куба

Объем куба равен кубу длины его грани.

Формула объема куба:

V = a3

где V - объем куба,
a - длина грани куба.

Объемы подобных тел

Пусть даны два подобных куба Q1 и Q2 (Рис.6), которые имеют измерения Q1:a,b,c и Q2:ka,kb,kc c коэффициентом подобия k соответственно.

Тогда объем куба Q1 равен V1 = abc,
а объем куба Q2 равен V2 = ka kb kc = k3 abc = k3 V1.

Т.е. V2 = k3 V1

Следовательно, отношение объемов двух кубов равно k3

Если тело представляет собой многогранник, в основании которого лежит многоугольник, то его можно разбить на определенное колическтво призм. И общий объем будет равен сумме обемов всех призм. Так как отношение площадей равно k2, а отношение высот этих фигур равно k, то объемы двух подобных фигур будут равны:

V 1 = S1h + S2h + S3h + ... + Snh

Объем подобной фигуры:

V 2 = k2S1kh + k2S2kh + k2S3kh + ... + k2Snkh

Следовательно:

V 2 = k2k (S1h + S2h + S3h + ... + Snh)

или
V 2 = k3 V1

Точно так же можно разбить тело на несколько пирамид. Тогда объем всего тела будет равен сумме всех составляющих его пирамид.

Отсюда можно сделать следующий вывод, что отношение объемов двух подобных тел равно кубу их коэффициента подобия.

Рис. 6 Объемы подобных тел.

3 сентября 2021г

Контрольная работа.

Задача 1. Осевое сечение цилиндра - квадрат. Площадь основания цилиндра равна 36π см². Найдите площадь полной поверхности цилиндра.

Задача 2. Высота конуса равна 6 см. Угол при вершине осевого сечения равен 120º.

а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 30º.

б) Найти площадь боковой поверхности конуса.

б) Найдём площадь боковой поверхности конуса. Для этого надо знать радиус конуса.

Задача 3. Диаметр шара равен 8. Через конец диаметра проведена плоскость под углом 45º к нему. Найдите длину линии пересечения сферы этой плоскостью.

Тема: Тела и поверхности вращения. Решение задач.

Тела вращения — это объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости. Шар — образован полукругом, вращающимся вокруг диаметра разреза.

Понятие о поверхностях и телах вращения

Если многоугольник ABCDE вращается вокруг прямой АВ (рис. 2.257), то каждая его точка, не принадлежащая прямой АВ, описывает окружность с центром на этой прямой. Весь многоугольник ABCDE при этом описывает некоторое тело вращения (рис. 2.258); прямая АВ — ось этого тела.

Плоскость, проходящая через ось тела вращения, является его плоскостью симметрии. Таких плоскостей каждое тело вращения имеет бесконечно много.

Любая плоскость, проходящая через ось тела вращения, пересекает это тело. Полученное сечение называют осевым сечением. В частности, осевое сечение тела вращения может состоять из двух изолированных друг от друга плоских фигур, симметричных относительно оси (рис. 2.259). Все осевые сечения тела вращения равны.

Чтобы задать тело вращения, достаточно указать его ось и фигуру, вращением которой получено данное тело. Описывая такое тело словесно, вместо оси иногда указывают принадлежащий ей отрезок. Например, вместо «тело, образованное вращением треугольника вокруг оси, содержащей его сторону» говорят и короче: «тело, образованное вращением треугольника вокруг его стороны».

Цилиндр

Можно дать определение цилиндра.

Определение. Цилиндром (точнее, круговым цилиндром) называют тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов — образующими цилиндра (рис. 2.260, 2.261).

Можно доказать, что основания цилиндра равны и лежат в параллельных плоскостях, что у цилиндра образующие параллельны и равны. Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Определение. Цилиндр называют прямым, если его образующие перпендикулярны плоскостям оснований.

На рисунке 2.261 изображен наклонный цилиндр, а на рис. 2.260 — прямой. В школьном курсе, как правило, рассматривают только прямые цилиндры, называя их для краткости просто цилиндрами.

Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из его сторон как оси (рис. 2.262).

Радиусом цилиндра называют радиус его основания. Высотой цилиндра называют расстояние между плоскостями оснований. Осью цилиндра называют прямую, проходящую через центры оснований. Ось цилиндра параллельна образующим.

Сечение цилиндра плоскостью, проходящей через ось цилиндра, называют осевым сечением цилиндра (рис. 2.263). Именно через такое сечение обозначают цилиндр. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра (рис. 2.264).

Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

На рисунке 2.265 изображено сечение цилиндра плоскостью, параллельной его оси. Оно представляет собой прямоугольник.

Если цилиндр с радиусом основания
разрезать по образующей (рис. 2.266) и развернуть на плоскости, получится прямоугольник, стороны которого — спрямленная окружность основания и образующая — развертка боковой поверхности цилиндра. Чтобы получить развертку полной поверхности, надо присоединить два круга — основания цилиндра (рис. 2.267).

Призма, вписанная в цилиндр и описанная около него

При решении геометрических задач часто приходится рассматривать комбинации многогранников и цилиндров, в частности, призм, вписанных в цилиндр и описанных около цилиндра.

Определение. Призмой, вписанной в цилиндр, называют такую призму, основания которой — равные многоугольники, вписанные в основания цилиндра. Ее боковые ребра являются образующими цилиндра (рис. 2.268).

Определение. Призму называют описанной около цилиндра, если ее основания — равные многоугольники, описанные около основания цилиндра. Плоскости ее граней касаются боковой поверхности цилиндра (рис. 2.269).

Конус

Определение. Конусом (точнее, круговым конусом) называют тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называют образующими конуса (рис. 2.272).

Поверхность конуса состоит из основания и боковой поверхности.

Определение. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (рис. 2.272).

На рисунке 2.273 изображен наклонный конус, в дальнейшем будет рассматриваться только прямой конус, называемый для краткости просто конусом.

Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис. 2.274).

Определение. Высотой конуса называют перпендикуляр, опущенный из его вершины на плоскость основания.

У прямого конуса основание высоты совпадает с центром основания (рис. 2.272). Осью прямого конуса называется прямая, содержащая его высоту. У наклонного конуса основание высоты может не совпадать с центром круга, лежащего в основания конуса (рис. 2.273).

Блог методиста ГБОУ СПО ЛНР "Комиссаровский колледж - агрофирма" Собко Натальи Анатольевны

Страницы403

205

Теоремы сложения и умножения вероятностей, формулы

Размещение элементов комбинаторики

Перестановка элементов комбинаторики

Комбинации или сочетание элементов комбинаторики

Перестановки и комбинации с повторениями

Примеры решения задач с элементами комбинаторики

Понятие о поверхностях и телах вращения

Цилиндр

Призма, вписанная в цилиндр и описанная около него

Конус

Комментариев нет:

Отправить комментарий

Поиск по этому блогу