305 новая

17 июня 2022 г.

Тема: Понятие об определенности интеграла. Формула Ньютона-Лейбница.

14 июня 2022 г.

Тема: Правила вычисления первообразных.

1. Первообразная суммы равна сумме первообразных. Если F(x) — первообразная для f(x), а G(x) — первообразная для g(x), то F(x) + G(x) — первообразная для f(x) + g(x).
2. Постоянный множитель можно выносить за знак производной. Если F(x) — первообразная для f(x), и k — постоянная, то k·F(x) — первообразная для k·f(x).
3. Если F(x) — первообразная для f(x), и k, b — постоянные, причём k ≠ 0, то 1/k · F(kx + b) — первообразная для f(kx + b).

 Запомни!

Любая функция F(x) = х2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.

 Например:

• F'(x) = (х2 + 1)' = 2x = f(x);

  f(x) = 2х , т.к. F'(x) = (х2 – 1)' = 2x = f(x);

  f(x) = 2х , т.к. F'(x) = (х2 –3)' = 2x = f(x);

• Связь между графиками функции и ее первообразной:

1. Если график функции f(x)>0 на промежутке, то график ее первообразной F(x) возрастает на этом промежутке.
2. Если график функции f(x)<0 на промежутке, то график ее первообразной F(x) убывает на этом промежутке.
3. Если f(x)=0, то график ее первообразной F(x) в этой точке меняется с возрастающего на убывающий (или наоборот).

Для обозначения первообразной используют знак неопределённого интеграла, то есть интеграла без указания пределов интегрирования.

11 июня 2022 г.

Тема: Первообразная. Первообразные элементарных функций.

Функцию у = F(x) называют первообразной для функции у = f(x) на промежутке X, если для любого х из X выполняется равенство F'(x) = f(x).

Примеры:

1.    Пусть . Тогда первообразная F(x) имеет вид , так как 

2.    Пусть f(x) = sin Зх. Тогда первообразная F(x) имеет вид  так как F'(x) = 

Для  в примере 1 мы нашли первообразную . Это не единственное решение задачи. Так, в качестве первообразной можно было взять и  (поскольку ), и  (поскольку ), и вообще любую функцию вида . Так же обстоит дело в примере 2, где в качестве первообразной можно было взять любую функцию вида 

Справедлива следующая теорема.

Теорема 13.

Если F(x) — первообразная для функции у = f(х) на промежутке X, то у функции у = f(х) бесконечно много первообразных и все эти первообразные имеют вид .F(x) + С, где С — любое действительное число.

Пример: 

Найти общий вид первообразных для функции у = f(x), где 

Решение: 

Одной из первообразных будет  , так как  Значит, общий вид первообразных таков:

Таблица первообразных

Учитывая, что отыскание первообразной есть операция, обратная дифференцированию, и отталкиваясь от таблицы производных (см. п. 210), получаем следующую таблицу первообразных (для простоты в таблице приведена одна первообразная F(x), а не общий вид первообразной F(x) + С):

Правила вычисления первообразных

Пусть нужно найти первообразную функции у = f(x). Иногда это можно сделать с помощью таблицы первообразных из п. 224; например, для функции  по второй строке указанной таблицы находим , т. е. , а общий вид первообразных 

Но чаще, прежде чем воспользоваться таблицей, приходится применять правила вычисления первообразных.

1°. Если F(x) — первообразная для f(x), а Н(х) — первообразная для h(x), то F(x) + Н(х) — первообразная для f(x) + h(x).

Иными словами, первообразная суммы равна сумме первообразных.

2°. Если F(x) — первообразная для f(x), a k — постоянная, то kF(x) — первообразная для kf(x).

Иными словами, постоянный множитель можно вынести за знак первообразной.

3°. Если F(x) — первообразная для f(x), a k, b — постоянные, причем , то  — первообразная для f(kx + b).

Пример 1.

Найти общий вид первообразных для функции у = f(x), где f(x) = 

Решение:

1) Воспользовавшись таблицей первообразных (см. п. 224), найдем первообразную для каждой из четырех функций, входящих в состав f(x):

2)    Воспользовавшись правилом 2°, получим, что для  первообразной будет , т. е.   для  первообразной будет , т. е. -3 cos х; для  первообразной будет , т. е.; для  первообразной будет , т. е. 

3)    Воспользовавшись правилом 1°, получим, что для f(x) первообразной будет

4)    Общий вид первообразных для заданной функции

Пример 2.

Найти общий вид первообразных для функции у = f(x), где 

Решение: 

Для  первообразной будет Тогда по правилу 3 для h(2x - 1) =

 первообразной будет 

Итак,  , а общий вид первообразных для заданной функции   

Интеграл

Пусть функция у = f(х) непрерывна на отрезке . Разобьем отрезок  на  частей точками  для однородности обозначений положим  (рис. 1.173).

Введем обозначения   и рассмотрим сумму

                      (1)

Ее называют интегральной суммой для функции у = f(x) по отрезку .

Наряду с интегральной суммой (1) рассматривают и интегральную сумму вида

      (2)

Отличие суммы (1) от суммы (2) состоит в том, что в первом случае на каждом из отрезков  выбирается значение функции в левом конце отрезка, а во втором случае — в правом.

На практике удобнее делить отрезок  на  равных частей. Тогда  и сумма (1) принимает вид  Значение суммы зависит

только от числа ; эту сумму можно обозначить  ( — греческая буква «сигма»).

Рассмотрим последовательность интегральных сумм

В математике установлено, что для непрерывной на отрезке  функции у = f(х) эта последовательность сходится (см. п. 200). Ее предел называют интегралом функции f(x) от  до  и обозначают  (читается «интеграл от  до  эф отикс дэ икс»). 

Итак,  Числа  и  называют соответственно нижним и верхним пределами интегрирования, знак  — знаком интеграла, функцию у = f(x) — подынтегральной функцией.

Пример: 

Найти 

Решение: 

Составим интегральную сумму  для функции у = f(x), где f(x) = х на отрезке [0; 1]. Для этого разобьем отрезок [0; 1] на  равных частей точками  (рис. 1.174).

Имеем:  Интегральная сумма  имеет вид

 

 

В числителе содержится сумма первых ( - 1) членов арифметической прогрессии, у которой первый член равен 1, а ( - 1)-й равен  - 1. Тогда сумма  вычисляется по формуле (см. п. 197)

В итоге получаем 

Далее имеем  Значит, 

10 июня 2022 г.

Тема: Применение производной для нахождения наибольших и наименьших значений. Примеры использования производной для нахождения наилучшего решения в прикладных задачах.

04 - 07 июня 2022 г.

Тема: Исследование функции с помощью производной.

Определение: Функция y = f(x) называется возрастающей (убывающей) на [ab], если таких, что x₁ < x₂, f(x₁) < f(x₂) ( f(x₁) > f(x₂) ).

Теорема 1. Если функция f(x), дифференцируемая на [ab], возрастает на этом отрезке, то на [ab].

Если f(x) непрерывна на [ab] и дифференцируема на (ab), причем для a < x < b, то эта функция возрастает на отрезке [ab].

Замечание 1. Аналогичную теорему можно доказать и для убывающей функции: Если f(x) убывает на [ab], то на [ab]. Если на (ab), то f(x) убывает на [ab].

Замечание 2. Геометрический смысл доказанной теоремы: если функция возрастает на отрезке [ab], то касательная к ее графику во всех точках на этом отрезке образует с осью Ох острый угол (или горизонтальна). Если же функция убывает на рассматриваемом отрезке, то касательная к графику этой функции образует с осью Ох тупой угол (или в некоторых точках параллельна оси Ох).

Теорема 2 (необходимое условие экстремума). Пусть функция f(x) задана в некоторой окрестности точки х₀. Если х₀ является точкой экстремума функции, то или не существует.

Примеры.

1. Функция y = x² имеет минимум при х = 0, причем (х²)′ = 2x = 0 при х = 0.

2. Минимум функции y = |x| достигается при х = 0, причем производная в этой точке не существует.

Замечание. Отметим еще раз, что теорема 2 дает необходимое, но не достаточное условие экстремума, то есть не во всех точках, в которых f ′(x) = 0, функция достигает экстремума.

Пример. У функции y = x³ y ′ = 3x² = 0 при х = 0, однако функция монотонно возрастает во всей области определения.

Определение: Если функция определена в некоторой окрестности точки х₀ и ее производная в этой точке равна нулю или не существует, точка х₀ называется критической точкой функции. Таким образом все точки экстремума находятся в множестве критических точек функции.

Теорема 3. Пусть функция f(x) непрерывна в некоторой окрестности точки х₀, дифференцируема в проколотой окрестности этой точки и с каждой стороны от данной точки f ′(x) сохраняет постоянный знак. Тогда:

1. если f ′(x) > 0 при x < x₀ и f ′(x) < 0 при x > x₀ , точка х₀ является точкой максимума;

2. если f ′(x) < 0 при x < x₀ и f ′(x) > 0 при x > x₀ , точка х₀ является точкой минимума;

3. если f ′(x) не меняет знак в точке х₀ , эта точка не является точкой экстремума.

Теорема 4. Пусть f ′(x₀) = 0 и у рассматриваемой функции существует непрерывная вторая производная в некоторой окрестности точки х₀. Тогда х₀ является точкой максимума, если f ′′(x₀) < 0, или точкой минимума, если f ′′(x₀) > 0.

Вывод: проверить наличие экстремума в критической точке можно тремя способами:

1. убедиться, что f ′(x) меняет знак при х = х₀ ;

2. определить знак f ′′(x₀) ;

3. если f ′′(x₀) = 0, исследовать порядок и знак производной, не обращающейся в 0 в рассматриваемой точке.

Пример.

Определим тип экстремума функции y = x³ - 3x + 7 при х = 1. Точка х = 1 является критической, так как y′ = 3x² - 3x = 0 при х = 1. Так как при x < 1 y ′ < 0, а при x > 1 y ′ > 0, x =1 – точка минимума. Можно было установить этот факт и с помощью второй производной: y ′′ = 6x – 3 = 3 > 0 при х = 1. Следовательно, функция в этой точке достигает минимума (теорема 4).

03 июня 2022 г.

Тема: Применение производной к исследованию функций и построению графиком.

Введем понятие производных высших порядков.

Пусть  - производная функции . Функция  называется также первой производной. Производная от  называется второй производной функции  и обозначается ,  или . Третьей производной функции  называется производная от , она обозначается ,  или . Вообще, -й производной от функции  называется производная от ее (-1)-й производной: . Говорят также, что  или  это производная порядка  от функции .

Если  - это фиксированная точка, то символ  обозначает производную -го порядка от функции  в точке . Для ее существования необходимо существование производной  не только в точке , но и в некоторой окрестности этой точки.

Например,  - степенная функция с произвольным (не равным нулю) показателем а. Первая производная . Если , то вторая производная . Если , то  и т.д. Таким образом, если а не является натуральным числом, то -я производная имеет вид:

 . (1)

Если же а - натуральное число, то формула (1) имеет смысл только для . Рассмотрим подробнее случай, когда а - натуральное число, а порядок производной . В этом случае формула (1) выглядит так:

.

Для натурального а в случае , очевидно, что -я производная от  равна нулю.

Пример №1

Пусть , тогда

Пример №2

Найдем производную порядка  показательной функции . Последовательно дифференцируя, имеем

.

В частности, если , то для любого  имеем .

Монотонность функции

Важным моментом является применение производной к исследованию возрастания и убывания функции.

Определение 1. Пусть  - промежуток числовой прямой, т.е.  - это отрезок, либо полуинтервал, либо интервал. Напомним, что функция  называется возрастающей (убывающей) на промежутке  , если для любых  при , верно неравенство

.

В этом случае  - промежуток монотонности функции. Если в последнем неравенстве допускается равенство, то функция называется неубывающей (невозрастающей) на  .

Например, функция, принимающая постоянное значение , является одновременно неубывающей и невозрастающей.

По знаку производной («0», «+», «-») можно судить о характере изменения функции на промежутке (const, возрастает, убывает).

Теорема 1. Пусть функция  непрерывна на промежутке , а ее производная  обращается тождественно в нуль внутри . Тогда  на .

Доказательство. Пусть  - две точки на промежутке . По теореме Лагранжа найдется точка , для которой

.

Так как , то точка  является внутренней точкой промежутка . По условию теоремы , поэтому . Следовательно,  принимает постоянное значение на промежутке .

Теорема 2. (достаточное условие возрастания и убывания функции). Пусть функция  непрерывна на промежутке , а ее производная   внутри  и не обращается тождественно в нуль ни на каком интервале из промежутка . Тогда  возрастает (убывает) на .

Доказательство. Приведем доказательство для случая возрастания функции.

Пусть , - две точки из промежутка . По теореме Лагранжа найдется точка , для которой

.

Так как , то точка  является внутренней точкой промежутка . По условию теоремы , поэтому . Таким образом, мы доказали, что функция  не убывает на промежутке . Следовательно, для любой точки  выполняются неравенства  и . Предположим, что . Тогда для любой точки  имеем , т.е.  на интервале , что противоречит условию теоремы. Поэтому , следовательно  возрастает на .

Для случая убывания ф

Экстремум функции

Важным понятием при исследовании функций является экстремум (от лат. extremum - крайний).

Определение 2. Точка  называется точкой локального максимума (минимума) функции , если для всех  из некоторой окрестности точки  выполняется неравенство (рис. 2):

 Рис. 2. Локальный максимум (слева) и минимум (справа)

Локальный (от лат. lokalis - местный) максимум (от лат. maximum - наибольший) и локальный минимум (от лат. minimum - наименьший) объединяются общим названием локальный экстремум. Очевидно, что у функции может быть несколько локальных максимумов и несколько локальных минимумов, причем некоторый локальный максимум может оказаться меньше какого-то локального минимума (рис. 3).

Теорема 3. (необходимое условие локального экстремума). Для того чтобы дифференцируемая функция  имела в точке  локальный экстремум, необходимо чтобы в этой точке выполнялось равенство .

Доказательство. Поскольку  - точка экстремума, то существует такой интервал , на котором  - наибольшее или наименьшее значение. Тогда по теореме Ферма 

 Рис. 3. Функция с несколькими локальными экстремумами

Определение 3. Точки, в которых производная функции обращается в нуль, называются cтационарными.

Из теоремы 3 следует, что точка локального экстремума дифференцируемой функции является стационарной точкой. Обратное утверждение неверно. Рассмотрим, например, функцию . Эта функция возрастает на всей числовой прямой и поэтому не имеет точек локального экстремума. В то же время точка  является стационарной точкой, так-как . То есть необходимое условие локального экстремума в точке  выполняется, но экстремума в ней нет.

Определение 4. Критической точкой функции  называется точка, в которой производная  либо равна нулю, либо не существует.

Заметим, что все стационарные точки функции будут и критическими.

Из определения и теоремы Ферма следует, что точка локального экстремума  является критической точкой функции , причем производная в точке  может и не существовать. Например, функция  имеет в точке  минимум, но не имеет в этой точке производной (рис. 4, а). Это совсем не означает, что любая точка, в которой функция не имеет производной, обязательно будет точкой локального экстремума. Например, функция  не является дифференцируемой в точке  и не имеет в этой точке экстремум (рис. 4, б). Ее производная имеет вид

.

Для наглядности построим и график функции  (рис. 4, в).

Таким образом, если функция имеет в точке локальный экстремум, то она является критической. Обратное утверждение неверно. Другими словами, точки локального экстремума нужно искать среди критических точек. В связи с этим критические точки часто называют точками возможного экстремума или точками, подозрительными на экстремум.

Рассмотрим критерии, позволяющие определять точки максимума и минимума из множества критических точек.

 Рис. 4. Графики функций: а) ; б) ; в) 

Теорема 4. (достаточное условие локального экстремума). Пусть  критическая точка функции , которая в этой точке непрерывна, и пусть существует окрестность  точки , в которой функция имеет производную , кроме, быть может, самой точки . Тогда:

1) если при переходе через точку  производная  меняет свой знак с плюса на минус, то точка  - точка локального максимума функции ;

2) если - с минуса на плюс, то  - точка локального минимума;

3) если в окрестности  производная имеет постоянный знак, то  не является точкой локального экстремума.

Доказательство. Рассмотрим случай 1). Пусть для некоторого  выполняются условия: ; . Тогда по теореме 2 на интервале  функция  возрастает и  для всех  из этого интервала, а на интервале  она убывает и . Согласно определения 2, точка  - точка локального максимума функции .

Случаи 2) и 3) доказываются аналогично функции, теорема доказывается аналогично.

31 мая 2022 г.

Тема: Наибольшее и наименьшее значения функции.

Наибольшее и наименьшее значения функции. Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке.

Основные термины: наибольшее значение функции, наименьшее значение функции, стационарная точка, критическая точка.

Говорят, что функция 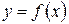 , определенная на промежутке  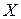, достигает на нём своего наибольшего (наименьшего) значения, если существует точка  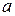, принадлежащая этому промежутку, такая, что для всех  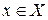выполняется неравенство  .

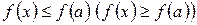Функция, непрерывная на отрезке, достигает на нём своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции 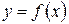 на отрезке  :

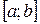1. найти  ;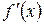

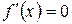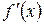2. найти точки, в которых  или  не существует, и отобрать из них те, что лежат внутри отрезка  ;

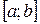3. вычислить значения функции 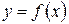 в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции  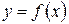на отрезке  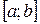, которые можно обозначить так:  ,  .

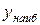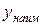Если поставлена задача найти 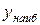 ,  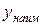для непрерывной на  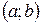функции  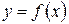, то она решается по тому же правилу, что соответствующая задача для отрезка  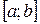. Отличие: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции 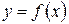 на промежутке  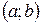полезны два утверждения:

1. если функция 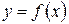 имеет в промежутке Хтолько одну точку экстремума  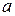, причём это точка максимума, то  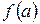– наибольшее значение функции на промежутке Х;

2. если функция 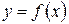 имеет в промежутке Х только одну точку экстремума  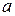, причём это точка минимума, то  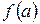- наименьшее значение функции на промежутке Х.

Пример 1.Исследовать функцию на наибольшее и наименьшее значение на заданном промежутке Х.

 .

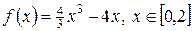Решение. Исследуемая функция дифференцируема и непрерывна на отрезке, поэтому

1. Найдем производную:  .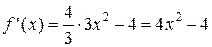

2. Найдём стационарные точки (в них производная обращается в нуль).

 ,

 .

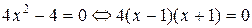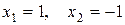Точки 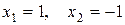 – точки возможного экстремума. При этом  ,  .

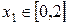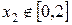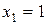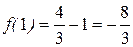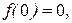
3. Найдём значения функции в точке  и на концах отрезка и выберем среди них наибольшее и наименьшее значения. Так как  ,   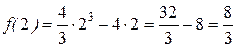, то  ,  .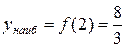

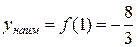Пример 2. Найти наибольшее значение функции  .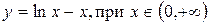

Решение.

1. Найдём производную функции:  .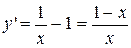

2. Найдём стационарные точки: 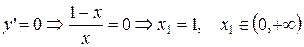 . В точке  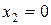– производная не существует, однако  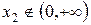. Таким образом, на заданном множестве существует единственная точка, подозрительная на экстремум.

28 мая 2022 г.

Тема: Исследование функции с помощью производной. Интервалы монотонности и точки экстремума.

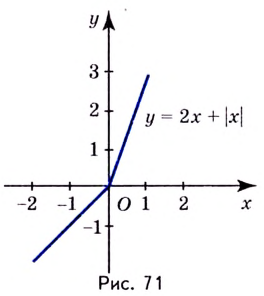
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).

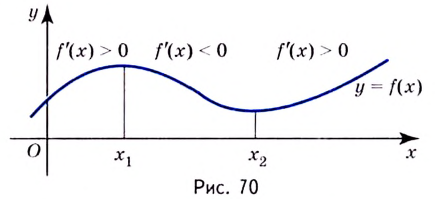
Правильными будут следующие утверждения.

• Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
• Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
• Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.

Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция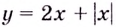 

Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.

Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.

Следовательно, чтобы определить промежутки возрастания и убывания функции 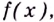 нужно решить неравенства  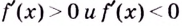или найти все критические точки функции,разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.    

Пример:

Найдите промежутки возрастания и убывания функции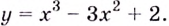 

Решение:

 

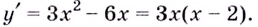
Уравнение 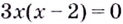 имеет корни  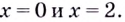Это — критические точки. Область определения данной функции — множество  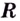— они разбивают на три промежутка:  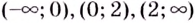(рис. 72). Производная функции на этих промежутках имеет соответственно такие знаки:  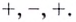Следовательно, данная функция на промежутках  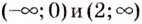возрастает, а на  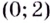убывает.

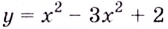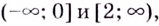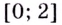Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция  в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках   на  — убывает.

Применение второй производной к исследованию функций и построению их графиков

При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.

Пусть функция 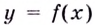 является дифференцируемой,  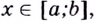её производная  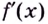— функция, которая также дифференцируема. Тогда можно найти производную  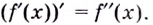Это производная второго порядка, или вторая производная функции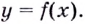 

Например, найти производную 2-го порядка функции 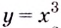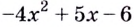означает найти производную этой функции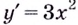 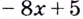 и полученную функцию продифференцировать: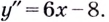 

Кривая 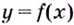 называется выпуклой на интервале  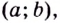если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1).

Кривая 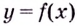 называется вогнутой на интервале  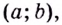если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2).

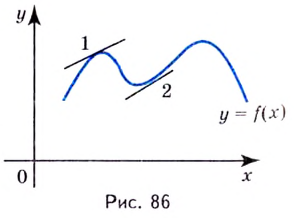
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.

Интервалы выпуклости и вогнутости находят при помощи такой теоремы.

Теорема. Если вторая производная дважды дифференцируемой функции 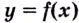 отрицательна  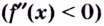на интервале  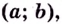то кривая 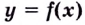выпуклая на данном интервале; если вторая производная функции 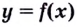положительная  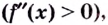то кривая вогнутая на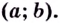 

Из теоремы следует, что точками перегиба кривой 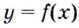 могут быть только точки, в которых вторая производная  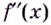равна нулю или не существует. Такие точки называют критическими точками второго рода.

Установим до статочное условие существования точки перегиба.

Теорема. Пусть 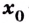 — критическая точка второго рода функции  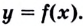Если при переходе через точку  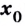производная  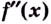меняет знак, то точка 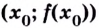является точкой перегиба кривой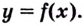 

Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:

1. найти область определения функции;
2. найти критические точки второго рода;
3. определить знак второй производной на образованных интервалах. Если 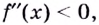 то кривая выпуклая; если  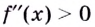— кривая вогнутая;
4. если производная 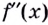 меняет знак при переходе через точку  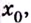то точка  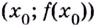является точкой перегиба кривой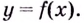 

Пример №1

Найдите интервалы выпуклости, вогнутости и точки перегиба кривой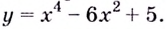 

Решение:

1) Область определения функции: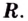 

2) Найдём вторую производную: 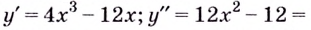 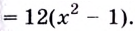Критические точки второго рода:  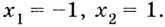Других критических точек нет.

3)    Разбиваем область определения на интервалы 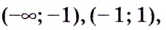 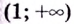и определяем знак второй производной на каждом из них.

Если 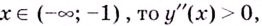 поэтому кривая вогнутая.

Если 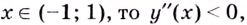 поэтому кривая выпуклая.

Если 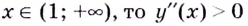 — кривая вогнутая.

Следовательно, точки 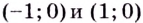 — точки перегиба кривой. Рассмотрим ещё один компонент в исследовании функций, благодаря которому упрощается построение некоторых графиков.

Тема: Вторя производная, ее геометрический и физический смысл.

Геометрический и физический смысл производной

Рассмотрим график непрерывной функции  и зафиксируем на нём точку  с координатами  Пусть точка также принадлежит графику, но не совпадает с точкой  Проведём секущую через точки 

Если при приближении точки  к точке  секущая, проведённая через эти две точки, стремится к некоторому предельному положению, то это предельное положение секущей называют касательной в точке  (левый рисунок).

Установим связь между касательной, проведённой в точке  и производной функции  в точке 

В дальнейшем величину  будем называть приращением аргумента, а величину  приращением функции 

Пусть  есть угол наклона секущей  угол наклона касательной.

Рассмотрим прямоугольный треугольник  (правый рисунок), где точка  имеет координаты 

Получим

Если приращение аргумента  устремить к нулю, то точка  будет стремиться к точке  и секущая будет стремиться к касательной. Следовательно,  будет стремиться к 

По определению, производная в точке  есть предел, к которому стремится отношение приращения функции  к приращению аргумента  при  стремящемся к нулю, запись такова:

И так как  стремится к  то значение производной равно угловому коэффициенту касательной.

В этом заключается геометрический смысл производной.

Физический смысл производной

Пусть точка движется вдоль координатной прямой и её координата в момент времени  определяется функцией  Рассмотрим промежуток времени  В момент времени  точка имеет координату  а в момент времени  координату  Значит, её перемещение за промежуток времени  равно  Разделив перемещение на промежуток времени, получим среднюю скорость движения за промежуток времени 

Предел средней скорости при  стремящемся к нулю, называют мгновенной скоростью движения в момент времени  Следовательно,

В общем случае, если какая-либо величина  изменяется по закону  то мгновенная скорость изменения этой величины при  равна  Таким образом, производная есть мгновенная скорость изменения функции. В этом заключается физический смысл производной. 

27 мая 2022 г.

Тема:Уравнение касательной к графику функции.

Построим кривую  (см. рис.1).

Рис. 1. График функции . 

Зафиксируем точку х=а. Если х=а, то значение функции равно  . Значит, имеем точку с координатами (.

Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой х=а, в которой - существует.

Уравнение касательной – это прямая, которая задается формулой 

Любая прямая, в том числе и касательная, определяется двумя числами:  и . Исходя из геометрического смысла производ­ной  (тангенс угла наклона касательной) – это есть угловой коэффициент .

Параметр  найдем из условия, что касательная проходит через точку (, то есть .

.

Стало быть . 

Запишем уравнение касательной

.

Или, .

Получили уравнение касательной к кривой  в точке с абсциссой .

2. Смысл элементов уравнения касательной

Смысл каждого элемента, который входит в уравнение касательной.

1) ( – точка касания касательной и графика функции.

2)  - угловой коэффициент касательной к графику функции.

3)  – произвольная точка на касательной.

Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что  – это произвольная точка на касательной.

Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.

3. Алгоритм составления уравнения касательной к графику функции

Задача.

К кривой  в точке с абсциссой  провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).

Рис. 2. Касательная к графику функции .

Зафиксируем точку . Значение функции в этой точке равно 1.

Алгоритм составления уравнения касательной к графику функции:

1) Найти  и точку касания.

- дано.Точка касания: (;.

2) Найти производную в любой точке . 

.

3) Найти значение производной в точке с абсциссой .

4) Выписать и проанализировать уравнение касательной.

.

Упрощаем и получаем: .

Ответ: .

4. Сопутствующие задачи

Задача 1.

Пусть дано уравнение касательной .

Найдите точки пересечения касательной с осями координат.

Если , то  . – это первая точка.

Если , то .  - вторая точка.

Итак, первая точка – это точка  с координатами  . Вторая точка – точка пересечения с осью , точка  с координатами  (см. рис.3).

Рис.3. Точки пересечения касательной к графику функции  с осями координат. Задача 2.

Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .

Рассмотрим прямоугольный треугольник  (Рис. 3). Длина катета  равна 1. Длина катета  . Длину отрезка  из прямоугольного треугольника найдем по теореме Пифагора:

Задача 3.

Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника  (Рис. 3) - площадь треугольника, образованного касательной и осями координат.

Следующая задача для самостоятельного решения.

Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .

5. Касательная к графику тригонометрической функции

Рассмотрим пример.

Дана функция .  Написать уравнение касательной к данной кривой в точке с данной абсциссой.

Рассмотрим графическую иллюстрацию (см. рис.4).

Рис. 4. Касательная к графику функции .

Нахождение точки касания.

1. Точка касания имеет координаты .

2. Найти . 

3. Найти 

И, последнее действие, – написать уравнение касательной.

4. . 

Упростим и получим . 

Заметим в точке (0;0) синусоида и касательная соприкасаются. В районе точки х=0 синусоида и прямая почти не различаются.

Тема: Геометрический смысл производной. 

Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f ( x ):

Из рисунка видно, что для любых двух точек A и B графика функции: f(x0+Δx)/f(x0)Δx=tgα, где  - угол наклона секущей AB. 

Таким образом, разностное отношение равно угловому коэффициенту секущей. 

Если зафиксировать точку A и двигать по направлению к ней точку B, то Δx неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. 

Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

Уравнение касательной к графику функции y=f(x) в точке x0:

24 мая 2022 г.

Тема: Производные сложной и обратной функций.

Производная сложной функции

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x ² + ln x. Получится f(x) = sin (x ² + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f ’(x) = f ’(t) · t ’, если x заменяется на t(x).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Задача. Найти производные функций: f(x) = e ^{2x + 3}; g(x) = sin (x ² + ln x)

Заметим, что если в функции f(x) вместо выражения 2x + 3 будет просто x, то получится элементарная функция f(x) = e ^x . Поэтому делаем замену: пусть 2x + 3 = t, f(x) = f(t) = e ^t . Ищем производную сложной функции по формуле:

f ’(x) = f ’(t) · t ’ = (e ^t )’ · t ’ = e ^t · t ’

А теперь — внимание! Выполняем обратную замену: t = 2x + 3. Получим:

f ’(x) = e ^t · t ’ = e ^{2x + 3} · (2x + 3)’ = e ^{2x + 3} · 2 = 2 · e ^{2x + 3}

Теперь разберемся с функцией g(x). Очевидно, надо заменить x ² + ln x = t. Имеем:

g ’(x) = g ’(t) · t ’ = (sin t)’ · t ’ = cos t · t ’

Обратная замена: t = x ² + ln x. Тогда:

g ’(x) = cos (x ² + ln x) · (x ² + ln x)’ = cos (x ² + ln x) · (2x + 1/x).

Вот и все! Как видно из последнего выражения, вся задача свелась к вычислению производной суммы.

Ответ:
f ’(x) = 2 · e ^{2x + 3};
g ’(x) = (2x + 1/x) · cos (x ² + ln x).

Очень часто на своих уроках вместо термина «производная» я использую слово «штрих». Например, штрих от суммы равен сумме штрихов. Так понятнее? Ну, вот и хорошо.

Таким образом, вычисление производной сводится к избавлению от этих самых штрихов по правилам, рассмотренным выше. В качестве последнего примера вернемся к производной степени с рациональным показателем:

(x ⁿ )’ = n · x ^{n − 1}

Немногие знают, что в роли n вполне может выступать дробное число. Например, корень — это x ^0,5. А что, если под корнем будет стоять что-нибудь навороченное? Снова получится сложная функция — такие конструкции любят давать на контрольных работах и экзаменах.

Задача. Найти производную функции:

Для начала перепишем корень в виде степени с рациональным показателем:

f(x) = (x ² + 8x − 7)^0,5.

Теперь делаем замену: пусть x ² + 8x − 7 = t. Находим производную по формуле:

f ’(x) = f ’(t) · t ’ = (t ^0,5)’ · t ’ = 0,5 · t ^−0,5 · t ’.

Делаем обратную замену: t = x ² + 8x − 7. Имеем:

f ’(x) = 0,5 · (x ² + 8x − 7)^−0,5 · (x ² + 8x − 7)’ = 0,5 · (2x + 8) · (x ² + 8x − 7)^−0,5.

Наконец, возвращаемся к корням:

 

23 мая 2022 г.

Тема: Производная суммы, разности, частного и произведения.

Производная произведения

Математика — наука логичная, поэтому многие считают, что если производная суммы равна сумме производных, то производная произведения strike">равна произведению производных. А вот фиг вам! Производная произведения считается совсем по другой формуле. А именно:

(f · g) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Задача. Найти производные функций: f(x) = x ³ · cos x; g(x) = (x ² + 7x − 7) · e ^x .

Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’(x) = (x ³ · cos x)’ = (x ³)’ · cos x + x ³ · (cos x)’ = 3x ² · cos x + x ³ · (− sin x) = x ² · (3cos x − x · sin x)

У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’(x) = ((x ² + 7x − 7) · e ^x )’ = (x ² + 7x − 7)’ · e ^x + (x ² + 7x − 7) · (e ^x )’ = (2x + 7) · e ^x + (x ² + 7x − 7) · e ^x = e ^x · (2x + 7 + x ² + 7x −7) = (x ² + 9x) · e ^x = x(x + 9) · e ^x .

Ответ:
f ’(x) = x ² · (3cos x − x · sin x);
g ’(x) = x(x + 9) · e ^x .

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Производная частного

Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

 

Неслабо, да? Откуда взялся минус? Почему g ²? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

Задача. Найти производные функций:

В числителе и знаменателе каждой дроби стоят элементарные функции, поэтому все, что нам нужно — это формула производной частного:

 

По традиции, разложим числитель на множители — это значительно упростит ответ:

 

20 мая 2022 г.

Тема: Производная суммы, разности, частного и произведения.

Если следовать определению, то производная функции в точке — это предел отношения приращения функции Δy к приращению аргумента Δx:

Вроде бы все понятно. Но попробуйте посчитать по этой формуле, скажем, производную функции f(x) = x ² + (2x + 3) · e ^x · sin x. Если все делать по определению, то через пару страниц вычислений вы просто уснете. Поэтому существуют более простые и эффективные способы.

Для начала заметим, что из всего многообразия функций можно выделить так называемые элементарные функции. Это относительно простые выражения, производные которых давно вычислены и занесены в таблицу. Такие функции достаточно просто запомнить — вместе с их производными.

Производные элементарных функций

Элементарные функции — это все, что перечислено ниже. Производные этих функций надо знать наизусть. Тем более что заучить их совсем несложно — на то они и элементарные.

Итак, производные элементарных функций:

Название	Функция	Производная
Константа	f(x) = C, C ∈ R	0 (да-да, ноль!)
Степень с рациональным показателем	f(x) = x n	n · x n − 1
Синус	f(x) = sin x	cos x
Косинус	f(x) = cos x	− sin x (минус синус)
Тангенс	f(x) = tg x	1/cos2 x
Котангенс	f(x) = ctg x	− 1/sin2 x
Натуральный логарифм	f(x) = ln x	1/x
Произвольный логарифм	f(x) = log a x	1/(x · ln a)
Показательная функция	f(x) = e x	e x (ничего не изменилось)

Если элементарную функцию умножить на произвольную постоянную, то производная новой функции тоже легко считается:

(C · f)’ = C · f ’.

В общем, константы можно выносить за знак производной. Например:

(2x ³)’ = 2 · (x ³)’ = 2 · 3x ² = 6x ².

Очевидно, элементарные функции можно складывать друг с другом, умножать, делить — и многое другое. Так появятся новые функции, уже не особо элементарные, но тоже дифференцируемые по определенным правилам. Эти правила рассмотрены ниже.

Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

1. (f + g)’ = f ’ + g ’
2. (f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

Задача. Найти производные функций: f(x) = x ² + sin x; g(x) = x ⁴ + 2x ² − 3.

Функция f(x) — это сумма двух элементарных функций, поэтому:

f ’(x) = (x ² + sin x)’ = (x ²)’ + (sin x)’ = 2x + cos x;

Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):

g ’(x) = (x ⁴ + 2x ² − 3)’ = (x ⁴ + 2x ² + (−3))’ = (x ⁴)’ + (2x ²)’ + (−3)’ = 4x ³ + 4x + 0 = 4x · (x ² + 1).

Ответ:
f ’(x) = 2x + cos x;
g ’(x) = 4x · (x ² + 1).

17 - 18 мая 2022 г.

Тема: Производные основных элементарных функций.

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.

1. (ex) '= ex
2. (ekx+b) '=kekx+b
3. (ax) '=axlna
4. 
5. 
6. 
7. (sin x) '=cosx
8. (cos x) '= -sinx

Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.

1.Производная показательной функции.

Показательная функция f(x)=ax, где а>0, a ≠1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:

ax=exln a (1)

так как exln a= (eln a)х= ах.

Стоит отметить свойств о функции ех: производная данной функции равна ей самой

(ex) '= ex. (2)

Применяя правило дифференцирования сложной функции, получим:

(ekx+b) ' = kekx+b. (3)

Производная для ax:

(ax) ' = axlna. (4)

2.Производная логарифмической функции.

Логарифмическую функцию  с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода

 (5)

Производная функции lnх выражается формулой

 (6)

Применяя правило дифференцирования сложной функции, получаем

 (7)

 (8)

3.Производные тригонометрических функций.

Для тригонометрических функций справедливы следующие равенства:

(sin x)’=cosx (9)

(cos x)’= -sinx (10)

Примеры и разбор решения заданий тренировочного модуля

Найти производную:

1. f(x) = 3lnx

Решение: 

Ответ: 

1. f(x) = 3·e2x

Решение: (3e2x) ' = 3·2· e2x = 6 ·e2x

Ответ: 6 ·e2x

1. f(x) = 2x

Решение: (2x) ' = 2xln2

Ответ: 2xln2

1. 

Решение: 

Ответ: 

1. f(x) = sin (2x+1) - 3cos(1-x)

Решение: (sin (2x+1) - 3cos(1-x)) ' = 2cos(2x+1) - 3sin(1-x)

Ответ: 2cos(2x+1) - 3sin(1-x)

16 мая 2022 г.

Тема: Понятие о производной функции. Физический смысл производной. Общий метод нахождения производной.

Пример 1. Найти производную функции

.

Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.

.

Из таблицы производных выясняем, что производная "икса" равна единице, а производная синуса - косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:

.

Пример 2. Найти производную функции

.

Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:

Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.

Таблица производных простых функций

1. Производная константы (числа). Любого числа (1, 2, 5, 200...), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто
2. Производная независимой переменной. Чаще всего "икса". Всегда равна единице. Это тоже важно запомнить надолго
3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни.
4. Производная переменной в степени -1
5. Производная квадратного корня
6. Производная синуса
7. Производная косинуса
8. Производная тангенса
9. Производная котангенса
10. Производная арксинуса
11. Производная арккосинуса
12. Производная арктангенса
13. Производная арккотангенса
14. Производная натурального логарифма
15. Производная логарифмической функции
16. Производная экспоненты
17. Производная показательной функции

Правила дифференцирования

1. Производная суммы или разности
2. Производная произведения
2a. Производная выражения, умноженного на постоянный множитель
3. Производная частного
4. Производная сложной функции

Правило 1. Если функции

дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

причём

                          

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.

                              

Правило 2. Если функции

и

дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение

причём

                     

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой. 

Следствие 1. Постоянный множитель можно выносить за знак производной:

                          

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей:

                     

Правило 3. Если функции

и

дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём

                  

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

20 апреля 2022 г.

Тема: Понятие о производной функции. Физический смысл производной. Общий метод нахождения производной.

Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Изучая поведение функции y=f(x) около конкретной точки x0, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции.

Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.

Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Итак, x1-x0=Δx, значит, x1=x0+Δx.

f(x1)-f(x0)=Δy, значит, 

Δy=f(x0+Δx)-f(x0). (1)

Нельзя истолковывать термин "приращение" как "прирост".

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=1,9

Решение:

Δx= x1−x0=1,9-2=-0,1

Δf= f(1,9) –f(2)=1,92-22=-0,39

Ответ: Δx=-0,1; Δf =-0,39

Пример 2.

Найдем приращение Δx и Δf в точке x0, если f(x)= x2, x0=2 и х=2,1

Решение:

Δx= x1−x0=2,1-2=0,1

Δf= f(1,9) –f(2)=2,12-22=0,41

Ответ: Δx=0,1; Δf =0,41

Пример 3.

Найдем приращение Δf функции  в точке x0,если приращение аргумента равно x0.

Решение:

по формуле (1) находим:

.

Ответ: .

С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t0; t0+∆t]. Если точка движется по прямой и известна ее координата x(t), то

Эта формула верна и для ∆t<0 (для промежутка [t0+∆t; t0]).

Аналогично выражение  называют средней скорость изменения функции на промежутке с концами х0 и х0+∆х.

Определение. Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Обозначение: y’ или f’(x)

Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

Схема вычисления производной функции

1. Найти приращение функции на отрезке [x; x+Δx]:

∆y=y(x+∆x)-y(x)

1. Разделить приращение функции на приращение аргумента:

1. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

Пример 4.

Вычислить производную функции y=x2

Решение: Используем схему вычисления производной по действиям:

1. ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
2. 
3. 

Ответ: y’=2x.

Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).

Таким образом, скорость – есть производная от пути по времени.

Пример 5.

Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.

Решение:

найдем ∆t= 1-0,8=0,2

S(0,8)= 1-2·0,8= -0,6=S(t)

S(1)= 1-2·1= -1=S(t+∆t)

.

Ответ: .

Необходимое и достаточное условие дифференцируемости

Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

13 апреля 2022 г.

Тема: Бесконечно убывающая геометрическая прогрессия и ее сумма.

Определение:

Геометрическая прогрессия со знаменателем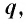 

Примеры бесконечно убывающих геометрических прогрессий

Приведем примеры бесконечно убывающих геометрических прогрессий.

Пример №1

Последовательность

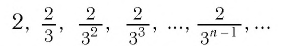
является бесконечно убывающей геометрической прогрессией с

первым членом 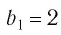и знаменателем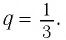 

Пример №2

Последовательность

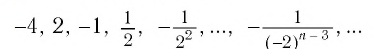
является бесконечно убывающей геометрической прогрессией с первым членом 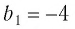 и знаменателем  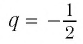(здесь 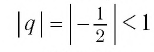). Изобразим четыре первых члена геометрической прогрессии из примера 1 на координатной прямой (рис. 1).

Мы видим, что чем больше номер прогрессии, тем ближе этот член к нулю, т.е. тем меньше его модуль, и с увеличением 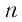 этот модуль становится меньше любого заданного положительного числа.

Например, если мы зададим число 0,01, то

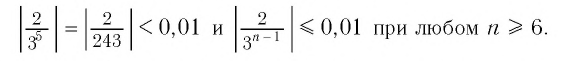
Изобразим 6 первых членов геометрической прогрессии из примера 2 на координатной прямой (рис. 2).

И в этом примере мы видим, что чем больше номер члена прогрессии, тем ближе этот член к нулю, т. е. тем меньше его модуль, и с увеличением п этот модуль становится меньше любого заданного положительного числа.

Например, если мы зададим число 0,001, то 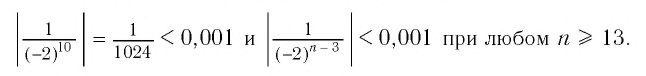 Такую же картину, как и в этих двух примерах, мы наблюдаем в любой бесконечно убывающей геометрической прогрессии  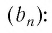чем больше номер п члена прогрессии  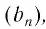тем меньше  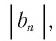и с увеличением  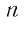этот, модуль становится меньше любого заданного положительного числа. Это утверждение формулируется еще и так:

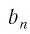 стремится к нулю при  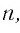стремящемся к бесконечности.

Заметим, что если 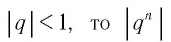стремится к нулю при 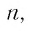стремящемся к бесконечности.

Рассмотрим бесконечно убывающую геометрическую прогрессию с первым членом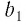 и знаменателем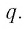 

Запишем формулу суммы первых 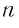 членов этой прогрессии и преобразуем это выражение:  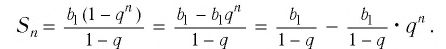Обозначим

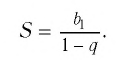
Тогда получим

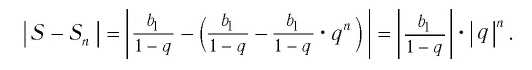
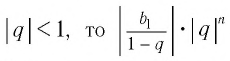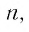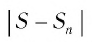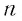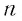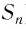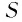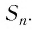Так как стремится к нулю при  стремящемся к бесконечности. Значит,  стремится к нулю при , стремящемся к бесконечности, т. е. чем больше число  (чем больше слагаемых в сумме ), тем меньше разница между  и  Поэтому число  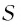называют суммой бесконечно убывающей геометрической прогрессии.

Пример №3

Найти сумму бесконечно убывающей геометрической прогрессии:

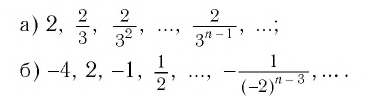
Решение:

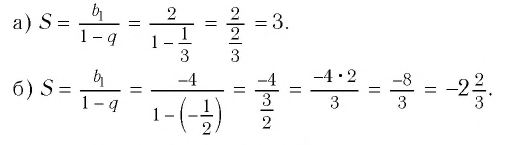
Ответ: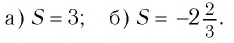 

Всё о бесконечно убывающей геометрической прогрессии

Пример:

Рассмотрим квадрат со стороной 1 (рис. 57). Если середины его противоположных сторон соединить отрезком, то возникнут два прямоугольника с площадью .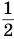

Если теперь середины одного из полученных прямоугольников соединить отрезком, то получится два прямоугольника с площадью 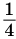. Снова повторив такое действие, получим два прямоугольника с площадью 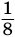. Будем продолжать этот процесс далее. В результате получим бесконечную убывающую последовательность

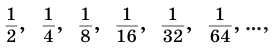
у которой каждый следующий член получается из предыдущего умножением на .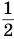

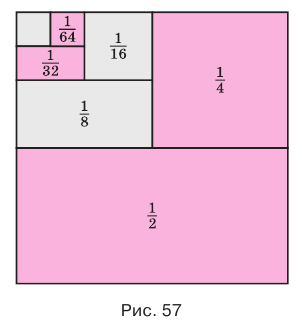
Естественно считать, что сумма 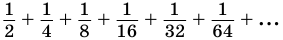 равна 1, так как она представляет площадь всего данного квадрата.

Записанная сумма содержит бесконечно много слагаемых. Рассмотрим ее часть 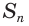 из 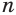 слагаемых:

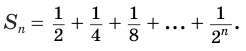
Ее компоненты образуют геометрическую прогрессию со знаменателем 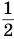. Поэтому

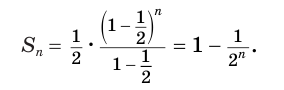
С возрастанием значения переменной 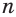 значение выражения  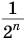становится все меньше и меньше: значение переменной  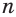всегда можно подобрать так, что значение выражения  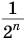станет меньше любого малого заранее выбранного числа. Поэтому бесконечную сумму  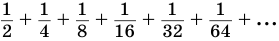считают равной 1.

Рассмотрим теперь бесконечную геометрическую прогрессию

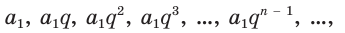
где 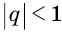. Для таких прогрессий истинно условие 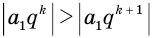, их называют бесконечно убывающими геометрическими прогрессиями.

Сумма бесконечно убывающей геометрической прогрессии

Суммой членов бесконечно убывающей геометрической прогрессии 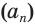 со знаменателем  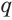называется число .

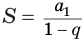Это определение объясняется тем, что с увеличением 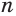 число 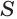 все меньше отличается от суммы первых  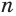членов этой прогрессии. Действительно,

.

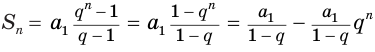Поскольку 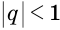, то 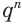 с увеличением  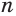приближается к нулю, а значит, приближается к нулю и вычитаемое 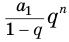. Поэтому сумма  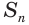приближается к .

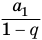Пример №4

Найдем значение суммы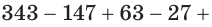 

.

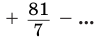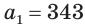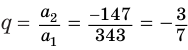Замечаем, что слагаемые этой алгебраической суммы являются членами бесконечно убывающей геометрической прогрессии, у которой  и . Поэтому

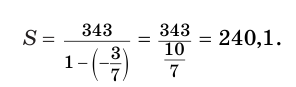
Мы знаем, что любое рациональное число можно представить десятичной дробью. При этом если разложение на простые множители знаменателя несократимой дроби, представляющей данное рациональное число, содержит только двойки и пятерки, то получается конечная десятичная дробь, а если это разложение содержит хотя бы один простой множитель, отличный от 2 и 5, то получается бесконечная периодическая десятичная дробь. Например:

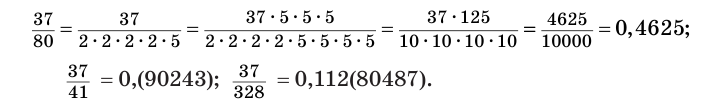
Повторяющаяся группа цифр называется периодом десятичной дроби, группа цифр между целой частью и периодом называется предпериодом. В записи 0,112(80487) предпериод равен 112, а период — 80 487.

Обыкновенную дробь можно преобразовать в десятичную делением ее числителя на знаменатель. Установим алгоритмы преобразования бесконечной периодической десятичной дроби в обыкновенную.

В дальнейшем мы будем пользоваться записью вида 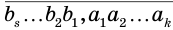. Она обозначает десятичную дробь, целая часть которой записана с помощью цифр 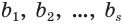, а дробная — с помощью цифр .

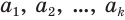Теорема 7.

Бесконечная периодическая десятичная дробь без предпериода равна обыкновенной дроби, числитель которой есть число, записанное цифрами периода, а знаменатель — число, записанное столькими девятками, сколько есть цифр в периоде.

Доказательство:

Пусть 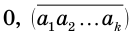 — периодическая десятичная дробь, где  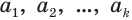— цифры периода. Тогда число  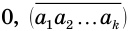можно представить бесконечной суммой:

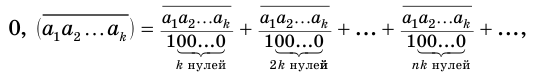
в которой каждое слагаемое получается из предыдущего умножением на 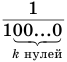. Это означает, что бесконечную периодическую дробь можно рассматривать как сумму  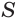членов бесконечно убывающей геометрической прогрессии с первым

членом 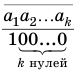 и знаменателем 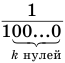. Поэтому

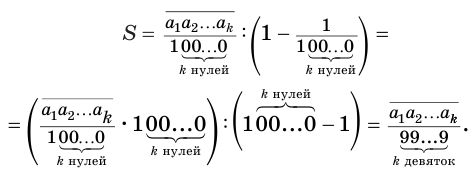
Теорема 7 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби без предпериода, который изображен схемой, приведенной на рисунке 58.

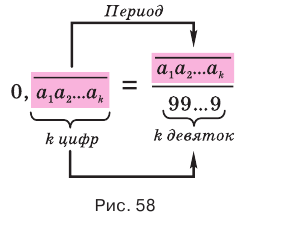
Пример №5

Представим обыкновенной дробью десятичную дробь 0,(9504). Имеем:

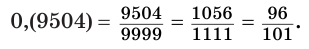
Теорема 8.

Бесконечная десятичная периодическая дробь с предпериодом равна обыкновенной дроби, числитель которой равен разности между числом, записанным цифрами от десятичной запятой до конца первого периода, и числом, записанным цифрами предпериода, а знаменатель — числу, записанному столькими девятками, сколько есть цифр в периоде, и столькими нулями, сколько есть цифр в предпериоде.

Доказательство:

Пусть 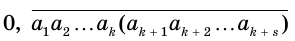 — периодическая десятичная дробь, где  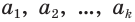— цифры предпериода,  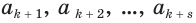— цифры периода. Тогда число  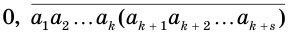можно представить суммой

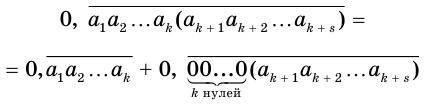
или, с учетом теоремы 7, суммой

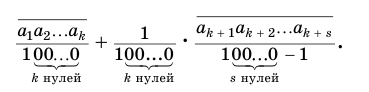
Преобразуем полученное выражение:

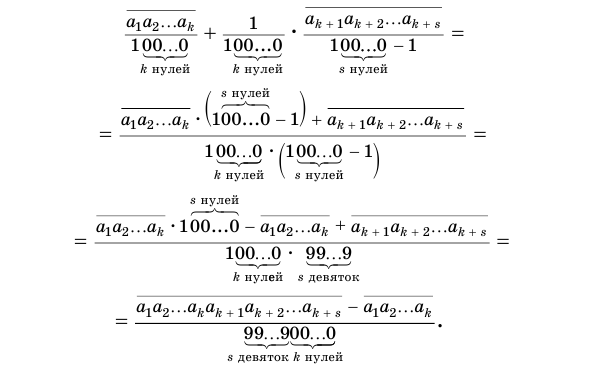
Теорема 8 обосновывает алгоритм представления обыкновенной дробью бесконечной периодической десятичной дроби с предпериодом. 

6 апреля 2022 г.

Тема: Суммирование последовательностей. Бесконечно геометрическая прогрессия и ее сумма.

Последовательностью называется функция, которая переводит множество натуральных чисел  в некоторое множество  : 

Элемент  называется первым членом последовательности,  - вторым, ... ,  - -ым или общим членом последовательности.

Пример 1.

Задание. Для последовательности  определить, чему равен третий член 

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для заданной последовательности имеем, что 

Ответ. 

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Пример 2.

Задание. Найти формулу общего члена последовательности 

Решение. Запишем каждый член последовательности в следующем виде:

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

Ответ. Формула общего члена: 

Пример 3.

Задание. Найти 15 член последовательности, заданной формулой -го члена: 

Решение. Для того чтобы найти  , подставим в формулу общего члена значение  . Получим:

Ответ. 

Пример 4.

Задание. Проверить, являются ли числа  и  членами последовательности

Решение. Число  является членом последовательности  , если существует такой номер  , что  :

Таким образом, число  является первым и пятым членами заданной последовательности.

Проверим теперь, является ли число  членом указанной последовательности  . Рассуждая аналогично, как и для  , получаем:

Таким образом, уравнение  не имеет решение в натуральных числах, а значит, не является членом последовательности 

Ответ. Число  является первым и пятым членами заданной последовательности, а  не является членом последовательности .

1. Последовательность задана аналитически, если задана формула ее n-го члена:

y_n = f(n).

Пример. y_n = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

30 марта 2022 г.

Тема: Контрольная работа

Тема: Последовательности. Способы задания. Свойства числовых последовательностей. Понятие о пределе последовательности, теоремы о пределах последовательностей. существование предела монотонной ограниченной последовательности.

Определение№1: множество чисел, каждое из которых снабжено своим номером, называется числовой последовательностью.

Элементы этого числового множества называются членами последовательности и обозначают: первый член - а ₁, второй - а ₂ , n- й член - а _n и т.д. Вся последовательность обозначается : а _1, а _2, а ₃, …, а _n или (а _n ).

Числовая последовательность представляет собой не что иное, как множество нумерованных чисел, упорядоченных наподобие натурального ряда, т.е. располагаемое в порядке возрастания номеров. Последовательность может содержать как конечное, так и бесконечное число членов.

Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, - бесконечной последовательностью.

Иногда бесконечную числовую последовательность вводят, используя понятие функции:

Определение №2: Функцию у = f(x), xN называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f(n), или у₁, у₂, у₃..., у_n или у(n).

Последовательности можно задавать различными способами, например, словесно, когда правило задавания последовательности описано словами, без указания формулы. Так, словесно задается последовательность простых чисел:

2,3,5,7,11,13,17,19,23,29,...

Особенно важны аналитический и рекуррентный способы задания последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее n-го члена.

Приведем три примера.

1. у_n= n². Это аналитическое задание последовательности

1,4,9,16,…, n², …

Указав конкретное значение n, нетрудно найти член последовательности с соответствующим номером. Если. Например, n= 9, то у₉ = 9² = 81, если

2. у_n= С. Здесь речь идет о последовательности С, С, С, …., С, …. . Такую последовательность называют постоянной (или стационарной).

3. у_n= 2ⁿ . Это аналитическое задание последовательности 2, 2², 2³, ….,2ⁿ, …

Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить n- й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия – это числовая последовательность (а_n), заданная рекуррентно соотношениями:

а _1, = а, а_n+1 = а_n+ d

(а и d – заданные числа, d – разность арифметической прогрессии)

Геометрическая прогрессия – это числовая последовательность (b_n)? Заданная рекуррентно соотношениями:

b _1, = b, b_n+1 = b_n·q

(b и q – заданные числа, b≠0, q ≠ 0; q знаменатель геометрической прогресси прогрессии).

Пример: Выписать первые пять членов последовательности, заданной рекуррентно:у₁ =1; у₂ = 1; у_n = у_n-2 + у_n-1

Решение. n –й член последовательности равен сумме двух предшествующих ему членов. Значит, последовательно получаем:

у₁ =1; у₂ = 1; у₃ =1+1 = 2; у₄ = 1+ 2 = 3; у₅ =2+3 =5; и т.д.

Ограниченные последовательности.

• Последовательность (х_n) называется ограниченной, если существуют такие два числа m и М, что для всех nN выполняется неравенство m≤ х_n ≤М.

• Последовательность (х_n) называется ограниченной сверху, если существует такое число М, что для всех nN выполняется неравенство х_n ≤М.

• Последовательность (х_n) называется ограниченной снизу, если существует такое число m, что для всех nN выполняется неравенство m≤ х_n

Например: последовательность (х_n), заданная формулой общего члена х_n= n, ограничена снизу (например, число 0) и не ограничена сверху.

Монотонные последовательности.

Последовательность (х_n) называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 > х_n.

Последовательность (х_n) называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 < х_n.

Последовательность (х_n) называется невозрастающей, если каждый ее член, начиная со второго, не более предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 ≤ х_n.

Последовательность (х_n) называется неубывающей, если каждый ее член, начиная со второго, не меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 ≥ х_n.

Возрастающие, убывающие, невозрастающие и неубывающие последовательности образуют класс монотонных последовательностей.

Предел числовой последовательности.

Рассмотрим для числовые последовательности – (у_n) и (x_n).

(у_n): 1, 3,5, 7, 9, … 2n – 1, …;

(x_n): 1, 

Изобразим члены этих последовательностей точками на координатной прямой.

0 1 3 5 7 9 11 у

0 0,25 0,5 1

Замечаем, что члены последовательности (x_n) как бы «сгущаются» около точки 0 – говорят последовательность сходятся , а у последовательности (у_n) такой точки сгущения нет – и говорят, что последовательность расходится.

Математики не используют термин точка сгущения, а они говорят предел последовательности.

Определение: Число b называется пределом последовательности (у_n), если в любой заранее выбранной окрестности точки b содержится все члены последовательности, начиная с некоторого номера.

Пишут так: у_n→b или  читают так: предел последовательности у_n при стремлении n к бесконечности равен b.

На практике используется еще одно истолкование равенства , связанное с приближенными вычислениями: если последовательность у_n = f(_n) сходится к числу b, то выполняется приближенное равенство f(_n)≈b, причем это приближенное равенство тем точнее, чем больше n.

Необходимое условие сходимости произвольной числовой последовательности:

Для того чтобы последовательность сходилась, необходимо, чтобы она была ограниченной.

Достаточное условие сходимости последовательности.

Если последовательность монотонна и ограничена, то она сходится. (теорема К.Вейерштрасса)

Свойства сходящихся последовательностей

1. Если последовательность сходится, то только к одному пределу.

2. Если последовательность сходится, то она ограничена.

3. Если последовательность монотонна и ограничена, то она сходится.

Если , то последовательность у_n= qⁿ расходится.

23 марта 2022 г.

Тема: Тела и поверхности вращения.

Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая, в свою очередь, ограничена кривой и крутится вокруг оси, лежащей в той же плоскости.

Какие же основные тела вращения существуют?

1. Шар. Это геометрическая фигура, которая образована в результате вращения полукруга вокруг диаметра разреза.
2. Цилиндр. Это геометрическая фигура, которая образована в результате вращения прямоугольника вокруг одной из его сторон.
3. Конус. Это геометрическая фигура, которая образована в результате вращения прямоугольного треугольника вокруг одного из своих катетов.
4. Тор. Это геометрическая фигура, которая образована в результате вращения окружности вокруг прямой, при этом окружность прямую не пересекает.

Стоит отметить такой интересный факт, что если вращаются контуры фигур, то у нас возникает поверхность вращения. Пример – сфера, которая образовывается в результате вращения окружности. Если же вращаются заполненные контуры, то у нас возникают тела. например, шар, который образовывается в результате вращения круга 9а круг. как всем известно, тело заполненное).

Тела вращения, разумеется, имеют свой объем и свою площадь. И то и другое, можно узнать с помощью теорем Гульдина-Паппа.

Первая теорема гласит о том, что площадь поверхности линии, которая образуется при вращении и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению длины линии на длину окружности, пробегаемой центром масс этой линии.

Вторая теорема говорит о том, что объем тела, который образуется при вращении фигуры и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры.

Тела вращения

Цилиндр

S   бок = 2πRh S   полн = 2πR 2   + 2πRh V = πR 2   h

Конус

S   бок = πRl S   полн = πR(R + l) V = 1 3 πR 2   h

Усеченный конус

S   бок = πl(R + r) S   полн = S   бок + π(R 2   + r 2   ) V = 1 3 πh(R 2   + Rr + r 2   )

Шар

S   сферы = 4πR 2   = πd 2   V = 4 3 πR 3   = 1 6 πd 3

Шаровой сектор

S = πR(2h + a) V = 2 3 πR 2   h

Шаровой сегмент

a 2   = h(2R - h) S   бок = 2πRh = π(a 2   + h 2   ) S   полн = π(2Rh + a 2   ) = π(h 2   + 2a 2   ) V = πh 2   (R - h 3 )

Шаровой пояс(слой)

V = 1 6 πh 3   + 1 2 π(a 2 1 + a 2 2 )h

16 марта 2022 г.

Тема: Шар и сфера. Сечение шара плоскостью. Касательная плоскость к сфере. Сфера, вписанная в многогранник. Сфера, описанная около многогранника.

Напомним, что шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии не большем заданного от некоторой данной точки. Эта точка – центр шара, а заданное расстояние – радиус шара.

Шар так же, как цилиндр и конус, является телом вращения. Он получается в результате вращения полукруга вокруг его диаметра.

Поверхность, образуемая при этом вращении полуокружности, называется сферой. Можно сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность есть граница круга, так и сфера – это граница шара.

Назовём элементы сферы и шара.

Радиус сферы – это отрезок, соединяющий центр сферы и любую её точку.

Хорда сферы – отрезок, соединяющий две точки сферы.

Диаметр сферы – хорда сферы, проходящая через её центр.

Радиус, хорда, диаметр шара – это радиус, хорда, диаметр его сферы.

Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Плоскость, которая проходит через центр шара, называется диаметральной плоскостью. Сечение ею шара – большим кругом, а сечение сферы – большой окружностью.

Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.

Плоскость, проходящая через точку А сферы и перпендикулярно радиусу, проведённому в эту точку, называется касательной плоскостью. Точка А называется точкой касания.

Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости.

Признак касательной плоскости к сфере: плоскость, перпендикулярная радиусу сферы в конечной его точке на сфере, является касательной к сфере.

Касательная плоскость пересекается с шаром в единственной точке – в точке касания.

Касательной прямой к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.

Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.

Линией пересечения двух сфер является окружность.

Площадь сферы радиуса : .

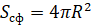Объём шара радиуса : .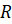

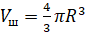Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Площадь боковой поверхности шарового сегмента:

 .

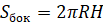Объём шарового сегмента:

,

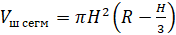где 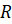 – радиус шара,  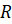– высота шарового сегмента.

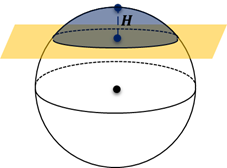
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.

Площадь боковой поверхности шарового сектора:

 .

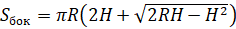Объём шарового сектора:

,

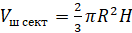где 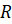 – радиус шара,  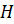– высота сегмента.

Шар называется вписанным в многогранник, а многогранник – описанным около шара, если поверхность шара касается всех граней многогранника.

Шар называется описанным около многогранника, а многогранник – вписанным в шар, если поверхность шара проходит через все вершины многогранника.

Шар называется вписанным в цилиндр, а цилиндр – описанным около шара, если поверхность шара касается оснований цилиндра и всех образующих.

Шар называется описанным около цилиндра, если окружности оснований цилиндра принадлежат поверхности шара.

Шар называется вписанным в конус (усечённый конус), а конус (усечённый конус) – описанным около шара, если поверхность шара касается основания (оснований) конуса и всех образующих.

Шар называется описанным около конуса (усечённого конуса), если окружность основания и вершина (окружности оснований) конуса принадлежат поверхности шара.

Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать шар.

Около пирамиды можно описать шар тогда и только тогда, когда около её основания можно описать окружность.

Если боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар.

В призму можно вписать шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение.

Описать шар около призмы можно тогда и только тогда, когда призма прямая и около её основания можно описать окружность.

16 февраля 2022 г.

Практическое занятие.

Задание №1. Найти стоимость металлической трубы, длина которой 10 м, а внутренний диаметр равен 30 см, если 1 м² трубы стоит 800 рублей.

Решение:

По условию задачи дан цилиндр высотой 10 м и с радиусом основания 15 см (рис. 1).

                                                                Рис. 1

 Так как необходимо вычислить стоимость металлической трубы в форме цилиндра, то нужно найти площадь боковой поверхности цилиндра. Воспользуемся формулой S_бок=2ПRh, так как R=15 cм, а h=10м=1000см, то искомая площадь равна S_бок=2П·15·1000=30000П см²=3 м². Найдем теперь стоимость металлической трубы: 3·800=2400 рублей.

Ответ: 2400 рублей.

 

Задание №2. Найти площадь полной поверхности выточенной детали в форме конуса, если площадь его осевого сечения известна и равна 12 дм², причем высота изделия равна 10 см.

 Решение:

Площадь полной поверхности конуса рассчитывается по формуле: S_полн=ПR(L+R), где L – длина образующей конуса, R – радиус основания конуса. По условию задачи известна высота конуса PO=10 см и S_сеч = 12 дм². Так как в осевом сечении конуса лежит равнобедренный треугольник, то его площадь вычисляется следующим образом:
S_сеч = 1/2·PO·AB, с другой стороны S_сеч = 12 дм², тогда получаем выражение
1/2·PO·AB= 12 дм², причем PO=10 см=1 дм, подставив в предыдущее выражение, получим уравнение: 1/2·1·AB= 12 дм², откуда AB= 24 дм. Так как R=OB=1/2AB, то R=1/2·24=12 дм.

 

                                                                  Рис. 2

Найдем теперь длину образующей L, из прямоугольного треугольника POB по теореме Пифагора имеем: , то есть , значит  дм. Теперь можно найти площадь полной поверхности конуса S_полн=П·12·(15,6+12)=331,2П дм².

Ответ: S_полн=331,2П дм²

 

Задание №3. Из заготовки в форме усеченного конуса с образующей 14 см, высотой 10 см и радиусом верхнего основания 8 см выточили деталь сферической формы радиуса 5 см. Вычислите площади полной поверхности заготовки и готового изделия.

Решение:

Найдем сначала площадь полной поверхности заготовки – усеченного конуса по формуле S_полн=ПL(r+R)+. По условию задачи известны: образующая
L=BC=14 см, высота H=OT=10 см, радиус верхнего основания r=OB=5 см. Необходимо найти еще радиус нижнего основания R=TC.

     Рис. 3

 Рассмотрим прямоугольник AOTK, у которого противоположные стороны равны, то есть AO = KT = r = 5 см, AK = OT = h =10 см, тогда в прямоугольном треугольнике AKD известны гипотенуза AD=14 см и катет AK=10 см, по теореме Пифагора найдем неизвестный катет DK. Итак, , ,  см, тогда радиус нижнего основания равен R=DK+KT=9,8+5=14,8 см.

Значит, площадь полной поверхности заготовки равна S_полн = П·14·(5+14,8)+.

Найдем теперь площадь поверхности готового изделия – шара радиуса 5 см используя формулу S_шара = 4ПR², получим S_шара = 4П5² = 100П см².

Ответ: S_{полн. заготовки} = , S_{готового изделия}  = 4П·5² = 100П см²

 

Тема: Решение задач.

9 февраля 2022 г.

Тема: Тела и поверхности вращения. Решение задач.

Основные формулы цилиндра:

Пусть R – радиус основания;

H – высота цилиндра, тогда

Sбок=2πRH

Sполн = Sбок+2Sосн=2πRH + +2πR 2 =2πR(R+H)

Основные формулы конуса:

Если R – радиус основания, H - высота, L– образующая конуса, то

Sбок=πRL

Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R )

Усеченный прямой конус:

h – высота усеченного конуса ; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая

Основные формулы шара:

R – радиус шара

Sсферы=4πR²

Задача 1.

Шар вписан в цилиндр. Площадь поверхности шара равна 111.

Найдите площадь полной поверхности цилиндра.

Решение.

Площадь полной поверхности цилиндра находим по формуле  S ц  = 2 πrh  + 2 πr 2 .

Из рисунка (1) для плоского

сечения видно, что радиус

основания цилиндра ( r ) равен

радиусу вписанного шара ( R ),

а его высота ( h ) равна диаметру

шара (удвоенному радиусу).

Поэтому  S ц  = 2 πR ·2 R  + 2 πR 2  = 6 πR 2 . Величину  πR 2  найдем из формулы поверхности шара  S ш  = 4 πR 2 . Следовательно,  πR 2  =  S ш  / 4 = 111/4. Окончательно находим  S ц  = 6·111 / 4 = 333/2 = 166,5.

Ответ:  166,5

Задача 2

В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

Дополним чертеж осевого сечения радиусом шара и расставим буквы для обозначения отрезков.  Площадь поверхности шара  S ш  = 4 πR 2  = 100π. Отсюда  R 2  = 25 и  R  = 5. В треугольнике  OAB :  OA  =  x  - половина искомой высоты цилиндра;  AB  = 4 - радиус основания цилиндра;  OB  = 5 - радиус шара.  По теореме Пифагора: x 2  + 4 2  = 5 2  ,

x 2  = 25 − 16 = 9;  x  = 3.  h  = 6.

Ответ:  6