4 февраля 2022 г.
Тема: Преобразование рациональных, иррациональных, степенных выражений.
Иррациональными выражениями называют выражения, содержащие операцию извлечения корня. Другими словами, иррациональные выражения – это выражения с радикалами (выражения, содержащие в своей записи знаки корня).
В записи
Свойства корней n а ≥ 0 b ≥ 0
1. Корень произведения равен произведению корней
Пример:
Вычислить
Решение:
Корень произведения равен произведению корней и наоборот: произведение корней с одинаковым показателем корня равно корню из произведения подкоренных выражений
Ответ:
2. Корень из дроби – это отдельно корень из числителя, отдельно из знаменателя
3. При возведении корня в степень, в эту степень возводится подкоренное выражение
4. Если
5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
6. Корень нечетной степени можно извлекать из положительных и отрицательных чисел, а корень четной степени – только из положительных.
7. Любой корень можно представить в виде степени с дробным (рациональным) показателем.
Пример:
Найдите значение выражения
Решение:
Корень произведения равен произведению корней
Корни из чисел мы можем извлечь сразу
Далее применим формулу
Корни
Ответ:
Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
Пример:
Найдите значение выражения
Решение:
Если над корнем не стоит показатель, то это означает, что мы работаем с квадратным корнем. Его показатель равен двум, т.е. четный. Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
Определим знак выражения, стоящего под знаком модуля, исходя из условия
Для проверки возьмем любое число из заданного промежутка, например,
Проверим знак каждого модуля
Ответ:
Свойства степеней с рациональным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
2. При возведении степени в степень основание остается прежним, а показатели перемножаются
3. При возведении в степень произведения в эту степень возводится каждый множитель
4. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
28 января 2022 г.
Тема: Преобразование логарифмических выражений.
Для преобразования логарифмических выражений необходимо помнить формулы и уметь их применять. Итак, формулы, которые нам понадобятся:
Свойства степеней;
Свойства логарифмов.
Для начала вспомним основные свойства логарифмов.
Свойства логарифмов
Вычислите:
Для первого слагаемого воспользуемся формулой перехода к новому основанию:
Пример .
Представить выражение в виде разности логарифмов:
Решение:
Упростим
Вернемся к первоначальному уравнению и подставим полученные результаты:
21 января 2022 г.
Тема: Преобразование показательных и логарифмических
выражений. Решение упражнений.
Логарифмические
выражения
Подавляющее
большинство задач B7 содержат логарифмы в том или ином виде. Эта тема
традиционно считается сложной, поскольку ее изучение приходится, как правило,
на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате
многие выпускники имеют весьма смутное представление о логарифмах.
Но в этой задаче никто
и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые
простые выражения, которые требуют незамысловатых рассуждений и вполне могут
быть освоены самостоятельно. Ниже приведены основные формулы, которые надо
знать, чтобы справиться с логарифмами:
1. loga x + loga y =
loga (x · y)
2. loga x − loga y =
loga (x : y)
3.
loga xn = n ·
loga x
Кроме того, надо уметь
заменять корни и дроби на степени с рациональным показателем, иначе в некоторых
выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:
Задача. Найти значения выражений:
log6 270 − log6 7,5
log5 775 − log5 6,2
Первые два выражения
преобразуются как разность логарифмов:
log6 270 − log6 7,5 = log6 (270
: 7,5) = log6 36 = 2;
log5 775 − log5 6,2 = log5 (775
: 6,2) = log5 125 = 3.
Для вычисления
третьего выражения придется выделять степени — как в основании, так и в
аргументе. Для начала найдем внутренний логарифм:
Затем — внешний:
Конструкции вида loga logb x многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. loga (logb x). Сначала вычисляется внутренний логарифм (положим logb x = c), а затем внешний: loga c.
Показательные
выражения
Будем называть
показательным выражением любую конструкцию вида ak, где
числа a и k — произвольные постоянные,
причем a > 0. Методы работы с такими выражениями достаточно
просты и рассматриваются на уроках алгебры 8-го класса.
Ниже приведены
основные формулы, которые обязательно надо знать. Применение этих формул на
практике, как правило, не вызывает проблем.
1.
an · am = an + m;
2.
an / am = an − m;
3.
(an)m = an · m;
4.
(a · b)n = an · bn;
5.
(a : b)n = an : bn.
Если встретилось
сложное выражение со степенями, и не понятно, как к нему подступиться,
используют универсальный прием — разложение на простые множители. В результате
большие числа в основаниях степеней заменяются простыми и понятными элементами.
Затем останется лишь применить указанные выше формулы — и задача будет решена.
Задача. Найти значения
выражений: 79 · 311 : 218, 247 :
36 : 165, 306 : 65 :
252.
Решение. Разложим все
основания степеней на простые множители:
79 · 311 : 218 = 79 ·
311 : (7 · 3)8 = 79 · 311 :
(78 · 38) = 79 · 311 :
78 : 38 = 7 · 33 = 189.
247 : 36 : 165 = (3 · 23)7 :
36 : (24)5 = 37 · 221 :
36 : 220 = 3 · 2 = 6.
306 : 65 : 252 = (5 · 3 · 2)6 :
(3 · 2)5 : (52)2 = 56 ·
36 · 26 : 35 : 25 :
54 = 52 · 3 · 2 = 150.
14 января 2022 г.
Тема: Правила действий с логарифмами. Решение примеров.
Свойства
логарифмов.
Итак, с ограничениями
на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться
со свойствами
логарифмов. Вот они:
Здесь всюду b>0 и c>0, а
также a>0, a≠1.
Вот такой вот
джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому
из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)
Начнём с первого
свойства:
Обычно это свойство именуют особо
- основным
логарифмическим тождеством. Откуда же оно берётся? Запишем
снова уже до боли знакомое нам равенство:
logab = c
Из самого определения
логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то
получим число b:
ac = b
А теперь подумаем, чему
же равно у нас число c?
Да вот же оно:
с = logab
Подставим это
выражение в предыдущее равенство и получим как раз то, что нам и
требуется:
"И зачем нам такая странная
перетасовка?" - спросите вы. А затем, что многоэтажное
выражение превращается в элементарное b!
Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.
Следующая группа формул
(2-3):
Думаю, тут комментарии
излишни. Всё прямо из определения логарифма следует.) И даже примеры
разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый
добрый способ — словесную
расшифровку. Проверено, помогает.)
Переходим к следующей группе формул (4-5):
Коротко эти формулы
называются логарифм
произведения и логарифм
частного (дроби).
А вот с их доказательствами вопрос
похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с
одинаковым основанием. Как именно? Мы с седьмого класса
помним, что при перемножении двух степеней с одинаковым основанием показатели
степеней складываются, а при делении — вычитаются:
Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:
m = logab
и
n = logac.
До
конца доказывать эти две формулы я не буду. Как продолжить доказательство?
Подставьте выражения для m и n в формулу
умножения степеней и воспользуйтесь основным
логарифмическим тождеством (формула №1). Попробуйте! Очень
полезно.)
Кстати, прошу обратить
внимание: данные формулы справедливы только при одинаковых основаниях!
Если основания разные, то, скорее всего, преобразования более мудрёные…
Идём дальше. Следующая
группа формул (6-7) — это формулы, позволяющие избавляться от степеней в
аргументе или в основании логарифма:
Смысл их тоже прост.
Если аргумент логарифма
возводится в степень, то показатель степени n можно вынести наружу и приписать
перед логарифмом. То же самое происходит и тогда, когда в степень
возводится основание логарифма,
только показатель степени переворачивается. Эти две полезные формулы избавляют нас
от степеней в аргументе/основании. Если это мешает, конечно. Это понятно.)
Тема: Переход к новому основанию.
Теорема
Если ![]() ,
, ![]() ,
, ![]() – положительные числа,
причем a и c отличны от 1, то имеет место
равенство:
– положительные числа,
причем a и c отличны от 1, то имеет место
равенство: ![]()
– формула перехода к
новому основанию
Доказательство
Преобразуем данное равенство, домножив левую и правую часть на знаменатель
правой части:
Далее возведем ![]() в степень левой и правой
части:
в степень левой и правой
части:
Преобразуем левую часть, применив свойство степеней:
Согласно основному логарифмическому тождеству:
Таким образом:
Согласно основному логарифмическому тождеству:
Следовательно:
Мы получили равенство, которое верно по основному логарифмическому тождеству. То есть:
Что и требовалось доказать.
Следствия из формулы перехода к
новому основанию
1. Первое следствие мы вывели попутно, доказывая формулу перехода:
2. Подставим в предыдущую формулу
оказательство
Докажем третье следствие из формулы перехода к новому основанию
, при
;
Доказательство
Прологарифмируем данное равенство по основанию ![]()
:
В правой и левой части вынесем степень за знак логарифма:
Так как
, то:
Согласно второму следствию из формулы перехода к новому основанию
, следовательно:
Домножим левую и правую часть на знаменатель правой части:
Равенство верное, следовательно:
Что и требовалось доказать.
Вычислите:
Решение
Разность логарифмов с одинаковым основанием – это логарифм частного, а
сумма логарифмов с одинаковым основанием – логарифм произведения. А у нас в
числителях и знаменателях стоят логарифмы с одинаковыми основаниями.
Применяя эти свойства, получаем:
Согласно формуле перехода к новому основанию
:
Следовательно:
Из основания логарифма показатель степени ![]()
выносится за знак
логарифма как ![]() , а из подлогарифмического
выражения – как
, а из подлогарифмического
выражения – как ![]() , то есть:
, то есть:
Следовательно:
27 декабря 2021 г.
Тема: Десятичный и натуральный логарифмы, число Е.
Десятичный логарифм числа – это логарифм по основанию 10 и пишут
вместо
.
 .
.
Натуральный логарифм числа – это логарифм этого числа по основанию
Остается вопрос, как находить значения логарифмов по другим основаниям?
Для этого вспомним основное логарифмическое тождество:
.
Прологарифмируем обе части по основанию с (т. е. вычислим логарифм по основанию с левой и правой части равенства.):
.
Применим свойство логарифма степени
:
.
Разделим обе части на ![]() :
: ![]() . Мы вывели формулу перехода к
новому основанию.
. Мы вывели формулу перехода к
новому основанию.
![]()
На заметку: ![]() и
и ![]() .
.
По формуле перехода к новому основанию приведем ![]() к десятичным и натуральным
логарифмам.
к десятичным и натуральным
логарифмам.
Формула перехода к десятичным логарифмам:
![]()
Формула перехода к натуральным логарифмам:
![]()
Пример 1. Вычислить ![]() . (Понадобится инженерный
миктокалькулятор)
. (Понадобится инженерный
миктокалькулятор)
1.
![]()
2.
![]()
Ответ: 3,99.
Пример 2. Решить уравнение:
![]()
1. Перейдем к одному основанию 5: ![]()
![]()
2. Одинаковый знаменатель ![]() .
.
![]()
3. Применим свойство логарифма частного:![]()
![]()
4. Дробь равна нулю, когда числитель равен нулю, знаменатель не равен нулю.
![]()
5. Воспользуемся определением логарифма.
![]()
6. Вычислим значение ![]()
![]()
![]()
Ответ: 0,5
Задача 1.
Вычислить ![]()
1.
перейдем к основанию 3 по формуле ![]()
2.
![]() , т. к.
, т. к. ![]()
![]()
1.
![]() .
.
![]()
Ответ: ![]()
Задача 2.
Вычислить ![]() .
.
1.
Используем свойство степеней ![]() .
.
2.
Заменим ![]() .
.
![]() =
=
![]()
1.
Применим основное логарифмическое тождество ![]()
![]()
Ответ: 50.
Тема: Логарифм произведения, частного, степени
Основное логарифмическое тождество
Среди всех остальных формул существует основное тождество, которое приводит к получению остальных свойств:

 Свойства логарифмов
Свойства логарифмов
1. Если имеется логарифм произведения двух чисел больших нуля, то данный логарифм можно записать в виде суммы:

Данное свойство вытекает из основного свойства степени - при умножении степеней их показатели складываются.
2. Логарифм частного двух чисел равен разности двух логарифмов:

Данное свойство было получено из свойства деления степеней - при делении степеней, показатели вычитаются.
3. Если некоторое число в степени находится под знаком логарифма, то показатель степени можно вынести вперед, тем самым, умножив логарифм на показатель:

Данное свойство вытекает из одного из основных свойств степенной функции - при возведении степени в степень показатели степеней перемножаются.
4. Если число и основание логарифма совпадает, то значение такого логарифма равно единице:

5. Логарифм по любому основанию равен нулю, если число равно единице:

6. При любом логарифме можно перейти от одного основания к другому. Для этого необходимо просто воспользоваться формулами:

20 декабря 2021 г.
Тема: Логарифм числа. Основное
логарифмическое тождество.
Определение
логарифма
Логарифмом положительного
числа ![]() по
основанию
по
основанию ![]() ,
, ![]() называется показатель
степени, в которую надо возвести
называется показатель
степени, в которую надо возвести ![]() чтобы получить
чтобы получить
Обратите
внимание: логарифм от неположительного числа не определен. Кроме того, в
основании логарифма должно быть положительное число, не равное 1. Например,
если мы возведем -2 в квадрат, получим число 4, но это не означает, что
логарифм по основанию -2 от 4 равен 2.
Понятие
логарифма и основного логарифмичесгого тождества
Понятие
логарифма и основного логарифмическое тождества состоят в тесной зависимости,
т.к. определение логарифма в математической записи и является основным
логарифмическим тождеством.
Основное
логарифмическое тождество вытекает из определения логарифма:
Определение
1
Логарифмом называют
показатель степени n, при возведении в которую числа а получают число b.
Замечание
1
Показательное
уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и
имеет единственный корень при положительном b. Этот корень
называется логарифмом числа b по основанию а и записывают:
Основное
логарифмическое тождество
При
условии, что a > 0, a ≠ 1, b > 0 можно
записать основное логарифмическое тождество
alogab = b
Примеры:
3log3 7 =
7
3-log3 7 = 1 3log3 7 = 1 7
4log2 7 =22
log2 7 = (2log2 7)2 = 72 = 49
21
+ log2 7 = 2 · 2log2 7 = 2 · 7 = 14
Что
такое логарифм и как его посчитать
где a – это основание
логарифма,
b
– это аргумент логарифма
Чтобы
узнать значение логарифма приравняем его к X.![]()
и преобразовываем в![]() и преобразовываем вЗапомните,
что именно основание (оно выделено красным) возводится в степень.
и преобразовываем вЗапомните,
что именно основание (оно выделено красным) возводится в степень.
Чтобы
было легче, можно запоминать так – основание всегда остается внизу (и в первом,
и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:
А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Еще
примеры:
Два очевидных следствия определения логарифма
log a a = 1 ( a > 0, a ≠ 1 )
(3)
log a 1 = 0 ( a > 0, a ≠ 1 )
(4)
Действительно,
при возведении числа a в первую степень мы получим то же самое число, а при
возведении в нулевую степень – единицу.
13 декабря 2021 г.
Тема: Решение показательных
уравнений. Решение примеров.
Показательные уравнения
Уравнение, содержащее переменную в показателе степени, называется показательным.
Простейшим примером показательного уравнения служит уравнение ах=b (a>0, а¹1).
Решение показательного уравнения вида af(x)=ag(x) (a>0, а¹1) основано на том, что это уравнение
равносильно уравнению f(x)=g(x).
Следствие. Пусть a>0, а¹1. Если степени с основанием а равны, то их показатели
равны, т.е. если as=at, то s=t.
Приведение обеих частей уравнения к
одному основанию
Этот способ основан на свойстве степеней: если две степени равны и их
основания равны, то равны и их показатели.
Пример 1. Решите уравнение
Решение.
Пример 2. Найдите корень уравнения
Решение. Перейдем к одному основанию степени:
Задание 1. Решите уравнение…
|
1) |
2) |
|||
|
7) 6х=1296 |
|
|
Пример 3. Решите уравнение
Решение. Данное уравнение равносильно уравнению
или
06 декабря 2021 г.
Тема: Действия над степенями с
рациональным и действительным показателем. Практическое занятие №1.
Определение. Степенью числа ![]()
с рациональным
показателем 
, где m-целое
число, а n-натуральное (![]() ), называется
число
), называется
число ![]() .
.
Свойства степени с рациональным показателем,
где r,s-рациональные числа, ![]() ,
,![]() .
.
Замечание. При ![]() рациональная степень
числа а не определяется.
рациональная степень
числа а не определяется.
Пример 1.
Пример 3.
Пример 4.
Пример 5.
Пример 6. Упростите выражение:
Решение:
=
 =
=
=
 =
=
=
2)Решить задание:
1. Найдите значение числового
выражения  .
.
4. Упростите выражение:
18 октября 2021 г.
Тема: Корни натуральной
степени из числа и их свойства. Корни и степени.
Корнем степени n из
действительного числа a, где n - натуральное число, называется
такое действительное число x, n-ая степень которого равна a.
Корень
степени n из числа a обозначается символом ![]() . Согласно этому
определению
. Согласно этому
определению ![]() .
.
Нахождение
корня n-ой степени из числа a называется извлечением корня.
Число а называется подкоренным числом (выражением), n -
показателем корня. При нечетном n существует корень n-ой степени
для любого действительного числа a. При четном n существует
корень n-ой степени только для неотрицательного числаa. Чтобы устранить
двузначность корня n-ой степени из числа a, вводится понятие
арифметического корня n-ой степени из числа a.
Понятие
арифметического корня степени N
Если ![]() и n -
натуральное число, большее 1, то существует, и только одно,
неотрицательное число х, такое, что выполняется равенство
и n -
натуральное число, большее 1, то существует, и только одно,
неотрицательное число х, такое, что выполняется равенство ![]() . Это
число х называется арифметическим корнем n-й степени из
неотрицательного числа а и обозначается
. Это
число х называется арифметическим корнем n-й степени из
неотрицательного числа а и обозначается ![]() .
Число а называется подкоренным числом, n - показателем
корня.
.
Число а называется подкоренным числом, n - показателем
корня.
Итак,
согласно определению запись ![]() , где
, где ![]() , означает,
во-первых, что
, означает,
во-первых, что ![]() и, во-вторых,
что
и, во-вторых,
что![]() , т.е.
, т.е. ![]() .
.
Понятие
степени с рациональным показателем
Степень
с натуральным показателем: пусть а - действительное число,
а n - натуральное число, большее единицы, n-й степенью
числа а называют произведение n множителей, каждый из
которых равен а, т.е. 
.
Число а - основание степени, n - показатель степени.
Степень с нулевым показателем: полагают по определению, если ![]() , то
, то ![]() . Нулевая степень
числа 0 не имеет смысла. Степень с отрицательным целым показателем:
полагают по определению, если
. Нулевая степень
числа 0 не имеет смысла. Степень с отрицательным целым показателем:
полагают по определению, если ![]() и n -
натуральное число, то
и n -
натуральное число, то ![]() . Степень с
дробным показателем: полагают по определению, если
. Степень с
дробным показателем: полагают по определению, если ![]() и n -
натуральное число, m - целое число, то
и n -
натуральное число, m - целое число, то ![]() .
.
Операции
с корнями.
Во
всех нижеприведенных формулах символ ![]() означает
арифметический корень (подкоренное выражение положительно).
означает
арифметический корень (подкоренное выражение положительно).
1.
Корень из произведения нескольких сомножителей равен произведению корней из
этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится:
5.
Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени
из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень
с отрицательным показателем. Степень некоторого числа с отрицательным (целым)
показателем определяется как единица, делённая на степень того же числа с
показателем, равным абсолютной величине отрицательного показателя:  Теперь
формула a m : a n = a m - n может быть
использована не только при m , большем, чем n , но и при m , меньшем, чем n .
Теперь
формула a m : a n = a m - n может быть
использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a4 : a7 = a 4 - 7 =
a -3 .
Если
мы хотим, чтобы формула a m : a n = a m -
n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень
с нулевым показателем. Степень любого ненулевого числа с нулевым показателем
равна 1.
П
р и м е р ы . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5
) 0 = 1
Степень
с дробным показателем. Для того, чтобы возвести действительное число а в
степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а
:
О
выражениях, не имеющих смысла. Есть несколько таких выражений.
Случай
1.![]() где a ≠ 0 , не
существует.
где a ≠ 0 , не
существует.
В
самом деле, если предположить, что x – некоторое число, то в соответствии с
определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит
условию: a ≠ 0
В
самом деле, если предположить, что это выражение равно некоторому числу x, то
согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет
место при любом числе x, что и требовалось доказать.
Случай
3
Если
считать, что правила действий со степенями распространяются и на степени с
нулевым основанием, то 0 0 - любое число.
Действительно,
Р е ш е н и е . Рассмотрим три основных случая:
1)
x = 0 – это значение не удовлетворяет данному уравнению
2)
при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует, что x – любое
число; но принимая во внимание, что в нашем случае x > 0 , ответом является x
> 0 ;
3)
при x < 0 получаем: – x / x = 1, т.e. –1 = 1, следовательно,
в
этом случае нет решения. Таким образом, x > 0.
11 октября 2021 г.
Тема: Степень с действительным
показателем и ее свойства. Решение задач.
Здесь символом
Определение-равенство (1) осмысленное только для тех
натуральных значений показателя ![]() , которые не меньше 2,
так как умножение есть двуместное действие. Поэтому натуральная степень
, которые не меньше 2,
так как умножение есть двуместное действие. Поэтому натуральная степень ![]() требует особого
определения, но такого, при котором сохраняются свойства натуральной степени, в
частности, свойство
требует особого
определения, но такого, при котором сохраняются свойства натуральной степени, в
частности, свойство ![]() . С учетом этого должно
быть:
. С учетом этого должно
быть: ![]() . Вместе с этим
. Вместе с этим ![]() . Поэтому первую
степень
. Поэтому первую
степень ![]() целесообразно
определить так:
целесообразно
определить так:
Так же, поскольку ![]() и вместе с
этим
и вместе с
этим ![]() , то нулевую
степень
, то нулевую
степень ![]() целесообразно
определить так:
целесообразно
определить так:
Обратив внимание, например, на то, что ![]() и вместе с
этим
и вместе с
этим
При этом, если в равенствах (1) и (2)
основание ![]() может иметь любое
действительное значение, то в равенствах (3) и (4) это значение должно быть
отличным от нуля.
может иметь любое
действительное значение, то в равенствах (3) и (4) это значение должно быть
отличным от нуля.
Рациональную степень ![]() с положительным
основанием
с положительным
основанием ![]() введем из
следующих соображений. Для целых показателей
введем из
следующих соображений. Для целых показателей ![]() и
и ![]() выполняется
свойство
выполняется
свойство ![]() . Желательно, чтобы оно
выполнялось и для дробных показателей. В таком случае будет
. Желательно, чтобы оно
выполнялось и для дробных показателей. В таком случае будет ![]() . Но равенство
. Но равенство ![]() означает, что
число
означает, что
число ![]() должно быть
корнем
должно быть
корнем ![]() -й степени из
числа
-й степени из
числа ![]() :
:
Примеры:
С учетом определения (5) получим:
Из определения степени с рациональным показателем
следует, что при любом положительном значении основания а и любом
рациональном значении показателя ![]() число
число ![]() является
положительным.
является
положительным.
Поскольку, с учетом свойств корня, ![]()
, то значение
рациональной степени а' не зависит от того, какой дробью из множества равных
дробей представлен рациональный показатель ![]() .
.
Если показателем степени является дробь ![]() с нечетным
знаменателем
с нечетным
знаменателем ![]() , определение (5)
распространяется и на отрицательные значения основания
, определение (5)
распространяется и на отрицательные значения основания ![]() .
.
Если показателем степени является дробь ![]() с четным
знаменателем
с четным
знаменателем ![]()
, то степень ![]() с отрицательным
основанием не определяется.
с отрицательным
основанием не определяется.
Степень ![]() положительного
числа
положительного
числа ![]() с иррациональным
показателем
с иррациональным
показателем ![]() определяется так.
определяется так.
Пусть ![]() . Для числа
. Для числа ![]() выпишем
последовательности
выпишем
последовательности
его десятичных приближений по недостатку и по избытку соответственно. Тогда
Из этих неравенств с учетом того, что если
Если значение переменной ![]() неограниченно
увеличивается, то значение выражения
неограниченно
увеличивается, то значение выражения ![]() стремится к нулю,
значение выражения
стремится к нулю,
значение выражения  — к единице, а
значение выражения
— к единице, а
значение выражения ![]()
, а потому и
выражения ![]() — к нулю. Это
означает, что значения выражений
— к нулю. Это
означает, что значения выражений ![]() и
и ![]() приближаются друг
к другу. Можно доказать, что есть только одно число
приближаются друг
к другу. Можно доказать, что есть только одно число![]() , для которого
, для которого ![]()
при всех ![]() . Оно и принимается в
качестве значения иррациональной степени
. Оно и принимается в
качестве значения иррациональной степени ![]() .
.![]() , где
, где ![]() и
и ![]() — рациональные
приближения иррационального числа
— рациональные
приближения иррационального числа ![]() по недостатку и
по избытку соответственно.
по недостатку и
по избытку соответственно.
04 октября 2021 г.
Тема: Степень. Степень с
рациональным показателем и её свойства.
Вам уже знакомы понятия степени числа с натуральным и целым показателями. Напомним, что степенью с натуральным показателем называется произведение
В свою очередь, степенью с отрицательным целым показателем называется
Однако
в алгебре существует ещё и понятие степени, у которой показатель не целое, а
дробное число. Итак, попытаемся записать![]() как некоторую
степень числа а, то есть
как некоторую
степень числа а, то есть ![]() .
.
Мы
знаем, что ![]() . Исходя из того, что
мы представили
. Исходя из того, что
мы представили ![]() , то получим, что
, то получим, что![]() . По свойству
возведения степени в степень имеем
. По свойству
возведения степени в степень имеем ![]() . Откуда видим, что
произведение
. Откуда видим, что
произведение ![]() . Следовательно,
. Следовательно, ![]() .
.
Тогда
получаем, что ![]() . По свойству
возведения корня n-й степени в степень получим, что
. По свойству
возведения корня n-й степени в степень получим, что ![]() .
.
Например,
Сделаем
вывод: если ![]() — натуральное
число, причём
— натуральное
число, причём ![]() ,
, ![]()
— целое число и
частное![]() является
целым числом, то при
является
целым числом, то при ![]()
справедливо
равенство ![]() .
.
Пусть ![]() , причём
, причём ![]() — целое
число. Отсюда
— целое
число. Отсюда ![]() . Тогда
. Тогда .
Если
же частное ![]() не является
целым числом, то степень числа а, где
не является
целым числом, то степень числа а, где ![]() , определяют так, чтобы
выполнялась формула
, определяют так, чтобы
выполнялась формула ![]() , то есть и в этом
случае считают, что
, то есть и в этом
случае считают, что![]() .
.
Таким
образом, формула ![]() справедлива для
любого целого числа
справедлива для
любого целого числа ![]() и любого натурального
числа
и любого натурального
числа ![]() и положительного
основания степени
и положительного
основания степени ![]() .
.
Например,
Напомним,
что рациональное число ![]() – это число
вида
– это число
вида ![]() , где
, где ![]()
– целое, ![]() – натуральное
число. Тогда по формуле
– натуральное
число. Тогда по формуле ![]()
получаем ![]() .
.
Таким
образом, степень определена для любого рационального показателя ![]()
и любого положительного
основания а.
Если
рациональное число ![]() , то выражение
, то выражение ![]() имеет смысл не
только при положительном основании степени, но и при
имеет смысл не
только при положительном основании степени, но и при ![]() , причём
, причём ![]() . Поэтому считают,
что
. Поэтому считают,
что![]() при
при ![]() .
.
Пользуясь
формулой ![]() , степень
с рациональным показателем можно представить в виде корня и наоборот.
, степень
с рациональным показателем можно представить в виде корня и наоборот.
Запомните! Степенью
числа![]() с рациональным
показателем
с рациональным
показателем ![]()
, где ![]() – целое число,
а
– целое число,
а ![]() – натуральное,
причём
– натуральное,
причём ![]() , называется
число
, называется
число ![]() .
.
Замечание: из
определения степени с рациональным показателем сразу следует, что
для любого ![]() и любого
рационального
и любого
рационального ![]() число
число ![]()
– положительно.
Любое
рациональное число допускает различные записи его в виде дроби. По основному
свойству дроби частное ![]() можно
представить, как частное
можно
представить, как частное ![]() , где
, где ![]() и
и ![]() – натуральные
числа,
– натуральные
числа, ![]() – целое число. Тогда
при любом
– целое число. Тогда
при любом ![]() справедливо
равенство
справедливо
равенство .
.
Что
легко доказать применяя свойства корней.
А
теперь перейдём к основным свойствам степени и покажем, что все свойства
степени с натуральным показателем верны для степени с любым рациональным
показателем и положительным основанием.
А
именно для любых рациональных чисел ![]() и
и ![]() и любых
и любых ![]()
и ![]() верны равенства:
верны равенства:
Для
доказательства этих свойств нужно воспользоваться определением степени
с рациональным показателем и свойствами корней.
Докажем
первое свойство.
Итак,
пусть ![]() ,
, ![]() , где
, где ![]() и
и ![]() – натуральные числа,
– натуральные числа, ![]() и
и ![]() – целые
числа.
– целые
числа.
Приведём
дроби к общему знаменателю ![]() ,
, ![]() .
.
По определению степени с рациональным показателем имеем
Аналогичным образом можно доказать и все остальные свойства степени с рациональным показателем.
А
теперь давайте приступим к практической части нашего урока.
Задание.
Найдите значения выражения ![]() .
.
Решение.
КОНТРОЛЬНАЯ
РАБОТА
3). Влажность сухой цементной смеси на складе составляет 18%. Во время перевозки из-за дождей влажность смеси повысилась на 2%. Найдите массу привезенной смеси, если со склада было отправлено 400 кг.
4). Вычислите |-9,6|+|-7,4|-2.
6).
3x4+ 9x4=
7).
-7x2 + 10x2=
01 октября 2021 г.
Тема: Многочлены от двух
переменных. Формулы сокращенного умножения. Проценты.
Формулы
сокращенного умножения с примерами
Складывать и вычитать многочлены достаточно просто. Оба эти действия рассматриваются вместе, поскольку осуществляются по одним и тем же принципам: Начинаем с правильной записи суммы или разности исходных многочленов. Для этого их надо заключить в скобки и поместить между ними нужный знак. Далее выполняем раскрытие скобок и получаем новый многочлен. После этого нужно привести многочлен к стандартному виду (если это необходимо). Поясним алгоритм примером.
Пример 1 Условие: выполните сложение и вычитание
двух многочленов x ⋅ y − x 2
+ 2 x·y−x2+2 и 7 ⋅ x 2 − 1
7·x2−1 .
Решение
Сначала выполним
сложение.
Записываем сумму: ( 7 ⋅ x 2 − 1
) + ( x ⋅ y − x 2 + 2 )
(7·x2−1)+(x·y−x2+2)
Раскрываем скобки и
получаем новый многочлен в следующей форме:
7 ⋅ x 2 − 1 + x ⋅ y − x 2 + 2 7·x2−1+x·y−x2+2
Нам осталось только привести результат к стандартному виду:
7 ⋅ x 2 − 1 + x ⋅ y − x 2 + 2 = 6 ⋅ x 2 + 1 + x ⋅ y 7·x2−1+x·y−x2+2=6·x2+1+x·y
Далее проводим вычитание по аналогии со сложением:
( 7 ⋅ x 2 − 1
) − ( x ⋅ y − x 2 + 2 ) = 7 ⋅ x 2 − 1 − x ⋅ y + x 2 − 2 = 8 ⋅ x 2 − 3 − x ⋅ y (7·x2−1)−(x·y−x2+2)=7·x2−1−x·y+x2−2=8·x2−3−x·y
Ответ:
(
7 ⋅ x 2 − 1 ) + ( x ⋅ y − x 2 + 2 ) = 6 ⋅ x 2 + 1 + x ⋅ y (7·x2−1)+(x·y−x2+2)=6·x2+1+x·y и ( 7 ⋅ x 2 − 1 ) − ( x ⋅ y − x 2 + 2 ) = 8 ⋅ x 2 − 3 − x ⋅ y (7·x2−1)−(x·y−x2+2)=8·x2−3−x·y.
Правила
умножения одного многочлена на другой
Перейдем к рассмотрению следующего действия – умножения.
Основное правило его
выполнения основано на распределительном свойстве умножения. С его помощью мы
можем свести умножение многочленов к последовательному перемножению всех их
членов друг на друга. Запишем правило:
Определение
1 Чтобы умножить один многочлен на другой, необходимо
выполнить умножение каждого члена первого множителя на каждый член второго
множителя, после чего провести сложение итоговых произведений. Результатом
умножения двух многочленов друг на друга будет новый многочлен.
Пример 2
Условие:
выполните умножение двух многочленов a − b a−b и −
3 ⋅ a + b −3·a+b.
Решение
Начнем с записи
произведения.
( a − b ) ⋅ ( − 3 ⋅ a + b )
(a−b)·(−3·a+b)
После этого нам нужно взять первый член первого многочлена
(т.е. a a) и перемножить его с каждым членом второго многочлена.
У нас получится
a ⋅ ( − 3 ⋅ a )
a·(−3·a) и a ⋅ b a·b.
То же самое проделаем и со вторым членом.
В итоге мы пришли к
произведениям − b ⋅ ( − 3 ⋅ a ) −b·(−3·a) и − b ⋅ b −b·b.
Теперь складываем все,
что у нас получилось:
a ⋅ ( − 3 ⋅ a ) + a ⋅ b − b ⋅ ( − 3 ⋅ a ) − b ⋅ b = − 3 ⋅ a 2 + 4 ⋅ a ⋅ b − b 2
a·(−3·a)+a·b−b·(−3·a)−b·b=−3·a2+4·a·b−b2
Вот запись всего решения:
( a − b ) ⋅ ( − 3 ⋅ a + b ) =
= a ⋅ ( − 3 ⋅ a ) + a ⋅ b − b ⋅ ( − 3 ⋅ a ) − b ⋅ b =
= − 3 ⋅ a 2 + 4 ⋅ a ⋅ b − b 2 (a−b)·(−3·a+b)=
=a·(−3·a)+a·b−b·(−3·a)−b·b=
=−3·a2+4·a·b−b2
Ответ: ( a − b ) ⋅ ( − 3 ⋅ a + b ) = − 3 ⋅ a 2 + 4 ⋅ a ⋅ b − b 2
(a−b)·(−3·a+b)=−3·a2+4·a·b−b2.
Правила возведения многочлена в степень .
После
того, как мы разобрались с правилами умножения многочленов, можем перейти к
возведению в натуральную степень. Это действие может быть приравнено к
умножению имеющегося многочлена на аналогичный столько раз, сколько
написано в показателе. Так, возведению 3 ⋅ x + 1
3·x+1 в степень 4 4 мы можем поставить в соответствие произведение 4 4-х
многочленов: ( 3 ⋅ x + 1 ) ⋅ ( 3 ⋅ x + 1 ) ⋅ ( 3 ⋅ x + 1 ) ⋅ ( 3 ⋅ x + 1 )
(3·x+1)·(3·x+1)·(3·x+1)·(3·x+1).
Пример 3
Условие:
выполните возведение многочлена 2 ⋅ a ⋅ b − b 3
2·a·b−b3 в квадрат.
Решение.
представим эту степень
как произведение двух одинаковых множителей и вычислим нужный результат.
( 2 ⋅ a ⋅ b − b 3
) 2 =
= ( 2 ⋅ a ⋅ b − b 3
) ⋅ ( 2 ⋅ a ⋅ b − b 3
) =
= 2 ⋅ a ⋅ b ⋅ ( 2 ⋅ a ⋅ b ) + 2 ⋅ a ⋅ b ⋅ ( − b 3 ) − b 3 ⋅ ( 2 ⋅ a ⋅ b ) − b 3 ⋅ ( − b 3 ) = =
4 ⋅ a 2 ⋅ b 2 − 4 ⋅ a ⋅ b 4 + b 6 (2·a·b−b3)2=
=(2·a·b−b3)·(2·a·b−b3)=
=2·a·b·(2·a·b)+2·a·b·(−b3)−b3·(2·a·b)−b3·(−b3)=
=4·a2·b2−4·a·b4+b6
Ответ: ( 2 ⋅ a ⋅ b − b 3 ) 2 = 4 ⋅ a 2 ⋅ b 2 − 4 ⋅ a ⋅ b 4 + b 6
(2·a·b−b3)2=4·a2·b2−4·a·b4+b6.
27 сентября 2021г
Тема: Многочлен от одной переменной. Делимость
многочленов. Деление многочленов с остатком. Число корней многочлена.
Деление
многочлена на одночлен
Чтобы
разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член
многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
Получили
привычное для нас деление одночленов. Выполним это деление:
Таким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.
При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В
нашем примере произведение полученного
многочлена 15xy2 + 10y + 5y2 и
делителя xy должно быть равно
многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному
делимому. Проверим так ли это:
(15xy2 + 10y + 5y2)xy =
15x2y3 + 10xy2 + 5xy3
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Если
мы вычислим выражение
![]()
При
этом выражение ![]() мы можем вернуть в исходное состояние
мы можем вернуть в исходное состояние
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n
Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d
Деление
одночлена на многочлен
Не
существует тождественного преобразования, позволяющего разделить одночлен на
многочлен.
Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.
Результатом
этого деления должен быть многочлен, перемножение которого с
многочленом 5x + 3y + 5 даёт одночлен 2xy.
Но не существует многочлена, перемножение которого с
многочленом 5x + 3y + 5 давало бы в результате
одночлен 2xy, поскольку перемножение многочленов даёт в результате
многочлен, а не одночлен.
Но
в учебниках можно встретить задания на нахождение значения выражения при
заданных значениях переменных. В исходных выражениях таких заданий бывает
выполнено деление одночлена на многочлен. В этом случае никаких преобразований
выполнять не нужно. Достаточно подставить значения переменных в исходное
выражение и вычислить получившееся числовое выражение.
Например,
найдём значение выражения
Выражение  представляет собой деление одночлена на
многочлен. В данном случае мы не сможем выполнить какие-либо преобразования.
Единственное, что мы сможем сделать — это подставить число 2 в исходное
выражение вместо переменной x и найти значение выражения:
представляет собой деление одночлена на
многочлен. В данном случае мы не сможем выполнить какие-либо преобразования.
Единственное, что мы сможем сделать — это подставить число 2 в исходное
выражение вместо переменной x и найти значение выражения:
Деление
многочлена на многочлен
Если
первый многочлен умножить на второй многочлен, получается третий многочлен.
Например, если умножить многочлен x + 5 на
многочлен x + 3, получается
многочлен x2 + 8x + 15
(x +
5)(x + 3) = x2 + 5x + 3x + 15
= x2 + 8x + 15
(x +
5)(x + 3) = x2 + 8x + 15
Если
произведение разделить на множитель, то получится множимое. Это правило
распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.
Деление
многочлена на многочлен выполняется уголком.
Отличие будет в том, что при делении многочленов не нужно определять первое
неполное делимое, как в случае деления обычных чисел.
Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.
В
данном случае результат нам известен заранее. Это будет
многочлен x + 5. Но чаще всего результат бывает неизвестным.
Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом
деления должен быть новый многочлен. Члены этого многочлена будут появляться
один за другим в процессе деления.
Сейчас
наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если
мы обратно разделим первый член третьего многочлена на первый член второго
многочлена, то получим первый член первого многочлена. А это то, что нам нужно.
Ведь мы должны прийти к многочлену x + 5.
Этот
же принцип нахождения первого члена будет выполняться и при решении других
задач на деление многочленов.
Итак,
чтобы найти первый член нового многочлена, нужно первый член делимого разделить
на первый член делителя.
Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Теперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15. Записываем этот многочлен под делимым 5x + 15
Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.
На
этом деление завершено.
После
выполнения деления можно выполнить проверку, умножив частное на делитель. В
нашем случае, если частное x + 5 умножить на
делитель x + 3, должен получаться
многочлен x2 + 8x + 15
(x +
5)(x + 3) = x2 + 5x + 3x + 15
= x2 + 8x + 15
Пример
2. Разделить многочлен x2 − 8x + 7 на
многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:
Умножаем x на x − 7, получаем x2 − 7x. Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое. Давайте воспользуемся этим методом:
Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним
проверку. Умножим частное x − 1 на
делитель x − 7. У нас должен получиться
многочлен x2 − 8x + 7
(x − 1)(x −
7) = x2 − x − 7x + 7
= x2 − 8x + 7
Пример 3. Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4
Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:
Получилось новое делимое 2x4 + 2x5. Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:
Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание
многочлена 2x4 + 2x5 из
многочлена 2x4 + 2x5 дало в результате 0, поэтому деление
успешно завершилось.
В
промежуточных вычислениях члены нового делимого располагались друг от друга,
образуя большие расстояния. Это было по причине того, что при умножении
частного на делитель, результаты были записаны так, чтобы подобные члены
располагались друг под другом.
Эти
расстояния между членами нового делимого образуются тогда, когда члены исходных
многочленов расположены беспорядочно. Поэтому перед делением желательно
упорядочить члены исходных многочленов в порядке убывания степеней. Тогда
решение примет более аккуратный и понятный вид.
Решим
предыдущий пример, упорядочив члены исходных многочленов в порядке убывания
степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить
в порядке убывания степеней, то получим
многочлен x7 + x6 + 2x5 + 2x4. А если члены
многочлена x2 + x3 упорядочить в порядке убывания степеней,
то получим многочлен x3 + x2
Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:
Деление завершено. Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Выполним
проверку. Умножим частное x4 + 2x2 на
делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5
(x4 +
2x2)(x2 + x3) = x4 (x2 + x3) +
2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
При
перемножении многочленов члены исходных многочленов тоже желательно
упорядочивать в порядке убывания степеней. Тогда члены полученного многочлена
тоже будут упорядочены в порядке убывания степеней.
Перепишем
умножение (x4 + 2x2)(x2 + x3) упорядочив члены
многочленов в порядке убывания степеней.
(x4 +
2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2)
= x7 + x6 + 2x5 + 2x4
Пример
4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на
многочлен 7 − 3x2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Значит,
Пример 5. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:
Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2
Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab. Записываем −2ab в частном:
Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4
Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче. Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3
Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.
Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4
Деление
многочлена на многочлен с остатком
Как
и при делении обычных чисел, при делении многочлена на многочлен может
образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное
число![]()
Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:
Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3
Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x3 − 6x2
Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4
Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x
Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4. Сразу вычтем этот полученный результат из делимого 10x + 4
Число
34, полученное в результате вычитания
многочлена 10x − 30 из многочлена 10x + 4,
является остатком. Мы не сможем найти следующий член частного, который при
умножении с делителем x − 3 дал бы нам в результате 34.
Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Когда
деление многочленов невозможно
Деление
многочлена на многочлен невозможно в случае, если степень делимого окажется
меньше степени делителя.
Например,
нельзя разделить многочлен x3 + x на
многочлен x4 + x2, поскольку делимое является многочленом
третьей степени, а делитель — многочленом четвёртой степени.
Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь
этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
Теперь
прямоугольник имеет длину x + 4 и
ширину x + 2. Площадь этого прямоугольника будет равна
произведению (x + 4)(x + 2) и выражаться
многочленом x2 + 6x + 8
(x + 4)(x + 2)
= x2 + 4x + 2x + 8
= x2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.
Степень
многочлена x2 + 6x + 8 равна сумме степеней
многочленов-сомножителей x + 4 и x + 2, а
значит ни одна из степеней многочленов-сомножителей не может превосходить
степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным,
степень делителя должна быть меньше степени делимого.
24 сентября 2021г
Тема: Тригонометрическая и
показательная формы комплексных чисел и действия над ними.
С
каждой точкой ![]() комплексной плоскости связан радиус-вектор
этой точки
комплексной плоскости связан радиус-вектор
этой точки ![]() , длина которого
, длина которого![]()
![]() и обозначается
и обозначается ![]() :
:
Угол ![]() образованный радиусом-вектором
образованный радиусом-вектором ![]() с осью
с осью ![]()
![]() и обозначается
и обозначается![]()
![]() выделяется главное значение
выделяется главное значение![]()
![]() Например,
Например, ![]()
Очевидно , что
Следовательно,
комплексное число![]() можно представить как
можно представить как
Представление
комплексного числа в виде (16.6), где
Сформулируем
некоторые свойства арифметических операций над комплексными числами.
1. При
сложении (вычитании) комплексных чисел их радиусы-векторы складываются
(вычитаются) по правилу параллелограмма.
На
рис. 16.2 показаны радиусы-векторы комплексных чисел
2. Модуль произведения (частного) двух комплексных чисел равен произ ведению (частному) модулей этих чисел, а его аргумент — сумме (разности) аргументов этих чисел, т.е.
Геометрически
умножение числа
Тема: Алгебраическая форма
комплексных чисел и алгебраические действия над ними.
Алгебраическая форма записи комплексных
чисел
Пусть x и y -
произвольные вещественные числа.
Множеством комплексных чисел называют множество
всевозможных пар (x, y) вещественных чисел, на котором
определены операции сложения, вычитания и умножения по правилам, описанным чуть
ниже.
Множество комплексных чисел является расширением
множества вещественных чисел, поскольку множество вещественных чисел содержится
в нём в виде пар (x, 0).
Комплексные числа, заданные парами (0, y),
называют чисто мнимыми числами.
Для комплексных чисел существует несколько форм записи:
алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная
(показательная) форма записи.
Алгебраическая форма - это такая форма
записи комплексных чисел, при которой комплексное число z, заданное
парой вещественных чисел (x, y), записывается в виде
|
z = x + i y . |
(1) |
где использован символ i , называемый мнимой единицей.
Число x называют вещественной
(реальной) частью комплексного числа z = x + i y
и обозначают Re z.
Число y называют мнимой частью
комплексного числа z = x + i y
и обозначают Im z.
Комплексные числа, у которых Im z = 0 ,
являются вещественными числами.
Комплексные числа, у которых Re z = 0 ,
являются чисто мнимыми числами.
Тригонометрическая и экспоненциальная формы записи
комплексных чисел будут изложены чуть позже.
Сложение, вычитание и умножение
комплексных чисел, записанных в алгебраической форме
Сложение и вычитание комплексных чисел z1 = x1 + i y1 и
z2 = x2 + i y2 осуществляется
по правилам сложения и вычитания
двучленов (многочленов) x1 + i y1
и x2 + i y2 ,
т.е. в соответствии с формулами
z1 + z2 = x1 + i
y1 + x2 + i y2 = x1 + x2 + i (y1 + y2)
,
z1 – z2 = x1 + i
y1– (x2 + i y2)
= x1– x2 + i (y1– y2)
.
Умножение комплексных чисел z1 = x1 + i y1 и
z2 = x2 + i y2 ,
так же, как и операции сложения и вычитания, осуществляется по правилам умножения
двучленов (многочленов), однако при этом учитывается важнейшее равенство,
имеющее вид:
|
i 2 = – 1 . |
(2) |
По этой причине
z1 z2 =
(x1 + i y1) (x2 + i
y2) = x1x2 + i
x1 y2 + i y1x2 + i 2 y1 y2 =
= x1x2 + i x1y2 + i y1x2 – y1 y2 = x1x2 – y1 y2 + i (x1 y2 + i x2 y1)
.
Два комплексных числа z = x + iy
и
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения, обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
Замечание. Если z
- вещественное число, то его модуль | z | равен
его абсолютной величине.
Деление комплексных
чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля
комплексное число z2 = x2 + i y2
осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Изображение
комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной
декартовой системой координат Oxy и
напомним, что радиус-вектором на плоскости называют вектор, начало которого
совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.
При таком представлении комплексных чисел сумме
комплексных чисел соответствует сумма радиус-векторов,
а произведению комплексного числа на вещественное число соответствует произведение
радиус–вектора на это число.
Рассмотрим радиус–вектор произвольного, но отличного
от нуля, комплексного числа z.
Аргументом комплексного числа z называют
угол φ между положительным направлением вещественной оси и
радиус-вектором z.
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным - в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не
имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k - произвольное целое число, то вводится, главное значение аргумента, обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y
нам известны его модуль r = | z | и
его аргумент φ, то мы можем найти вещественную и мнимую части по формулам
|
|
(3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y, то модуль этого числа, конечно же, определяется по формуле
|
|
(4) |
20 сентября 2021г
Тема: Действительная и мнимая
часть, модуль и аргумент комплексного числа.
Число r — длина радиус-вектора точки M (x, y)является модулем комплексного числа z = x + iy.
Обозначается как ![]()
Из рисунка получаем формулу для определения модуля числа, которое задано в алгебраической форме z = x + iy:
При помощи правила вычитания записываем модуль числа z = z1 – z2,
где z1 = x1 + iy1 и z2 = x2 + iy2:
![]()
А это является формулой для расстояния между точками![]()
![]()
Т.о., число ![]() - это расстояние между точками z1 и z2 на
комплексной плоскости.
- это расстояние между точками z1 и z2 на
комплексной плоскости.
Пример. Найдем модули комплексных чисел:
Рассчитаем решение для всех 3-х случаев:
1) z1 и z2 являются числами действительными, при этом
2) числа ![]() и
и ![]() являются чисто мнимыми, при этом
являются чисто мнимыми, при этом
Полярный угол φ точки M (x, y) является аргументом
комплексного числа z = x + iy. Обозначается
как ![]() .
.
Формулу для определения аргумента комплексного числа z = x + iy, который задан в алгебраической форме, получаем, пользуясь связью декартовых и полярных координат точки M (x, y).
Для точек, которые не лежат на мнимой оси, то есть для z, у
которых ![]()
![]()
![]() , получаем
, получаем ![]() ; для точек мнимой отрицательной полуоси, то есть для z,
у которых
; для точек мнимой отрицательной полуоси, то есть для z,
у которых ![]() , получаем
, получаем
Аргумент числа![]()
Определение аргумента при![]() сводится к решению тригонометрического уравнения
сводится к решению тригонометрического уравнения ![]() . При
. При ![]() , то есть когда
, то есть когда ![]() является числом действительным, у нас есть
является числом действительным, у нас есть ![]()
![]()
![]() при
при![]()
При ![]() решение уравнения зависимо от четверти плоскости
решение уравнения зависимо от четверти плоскости ![]() . Четверть, в которое расположена точка z,
определяют по знакам
. Четверть, в которое расположена точка z,
определяют по знакам ![]()
![]() . В итоге имеем:
. В итоге имеем:
При решении примеров удобно пользоваться схемой:
Пример. Найти аргументы чисел:
Решим задачу для каждого из 3-х случаев:
1) числа ![]() и
и ![]() — действительные, причем
— действительные, причем
2) числа ![]() и
и ![]() — чисто мнимые
— чисто мнимые ![]() , причем
, причем ![]()
![]()
![]() ;
;
3) для числа ![]() имеем
имеем![]()
Пример. Найти модуль и аргумент числа![]()
Находим ![]() . Т.к.
. Т.к. ![]() , то есть точка расположена в 4 четверти, то из
равенства
, то есть точка расположена в 4 четверти, то из
равенства ![]() получаем
получаем
17 сентября 2021г
Тема: Комплексные числа.
Геометрическая интерпретация комплексных чисел.
Одна из причин введения рациональных чисел
обусловлена требованием, чтобы всякое линейное уравнение ax = b (где
a № 0) было разрешимо. В области целых чисел линейное уравнение
разрешимо лишь в том случае, когда b делится нацело на a.
Одна из причин расширения множества
рациональных чисел до множества действительных чисел была связана с
разрешимостью квадратных уравнений, например, уравнения вида x2 =
2. На множестве рациональных чисел это уравнение не разрешимо, так как среди
рациональных нет числа, квадрат которого равен двум. Как известно, ![]() –
число иррациональное. На множестве же действительных чисел уравнение x2 =
2 разрешимо, оно имеет два решения x1 =
–
число иррациональное. На множестве же действительных чисел уравнение x2 =
2 разрешимо, оно имеет два решения x1 = ![]() и
x2 = –
и
x2 = – ![]() .
.
И все же нельзя считать, что на множестве
действительных чисел разрешимы все квадратные уравнения. Например, квадратное
уравнение x2 = – 1 на множестве действительных чисел решений не
имеет, так как среди действительных чисел нет такого числа, квадрат которого
отрицателен.
Таким образом, действительных чисел явно
недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках
которой каждое квадратное уравнение было бы разрешимо. Это соображение приводит
к необходимости вводить новые числа и расширять множество действительных чисел
до множества комплексных чисел, в котором было бы разрешимо любое квадратное
уравнение.
Вспомним о едином принципе расширения
числовых систем и поступим в соответствии с этим принципом.
Если множество А расширяется до множества
В, то должны быть выполнены следующие условия:
1.
Множество
А есть подмножество В.
2. Отношения элементов множества А (в частности, операции над ними)
определяются также и для элементов множества В;
смысл этих отношений для
элементов множества А, рассматриваемых уже как элементы множества В, должен
совпадать с тем, какой они имели в А до расширения.
3. В множестве В должна выполняться операция, которая в А была невыполнима или
не всегда выполнима.
4. Расширение В должно быть минимальным из всех расширений данного множества А,
обладающих первыми тремя свойствами, причем это расширение В должно
определяться множеством А однозначно (с точностью до изоморфизма).
Итак, расширяя множество действительных
чисел до множества новых чисел, названных комплексными, необходимо, чтобы:
а) комплексные числа подчинялись основным
свойствам действительных чисел, в частности, коммутативному, ассоциативному и
дистрибутивному законам;
б) в новом числовом множестве были разрешимы любые квадратные уравнения.
Множество действительных чисел
недостаточно обширно, чтобы в нем были бы разрешимы все квадратные уравнения.
Поэтому, расширяя множество действительных чисел до множества комплексных
чисел, мы потребуем, чтобы в нем можно было бы построить полную и законченную
теорию квадратных уравнений. Другими словами, мы расширим множество
действительных чисел до такого множества, в котором можно будет решить любое
квадратное уравнение. Так, уравнение x2 = – 1 не имеет решений
во множестве действительных чисел потому, что квадрат действительного числа не
может быть отрицательным. В новом числовом множестве оно должно иметь решение.
Для этого вводится такой специальный символ i, называемый мнимой единицей,
квадрат которого равен – 1.
Ниже будет показано, что введение этого
символа позволит осуществить расширение множества действительных чисел,
пополнив его мнимыми числами вида bi (где b – действительное число) таким
образом, чтобы в новом числовом множестве (множестве комплексных чисел) при
сохранении основных законов действительных чисел были разрешимы любые
квадратные уравнения.
Основные определения. Операции над
комплексными числами
1. Существует элемент i (мнимая единица)
такой, что i2 = – 1.
2. Символ a + bi называют комплексным
числом с действительной частью a и мнимой частью bi, где a и b – действительные
числа, b – коэффициент мнимой части.
Комплексное число a + 0i отождествляется с
действительным числом a, т.е. a + 0i = a, в частности, 0 + 0i = 0. Числа вида
bi (b № 0) называют чисто мнимыми.
Например, комплексное число 2 + 3i имеет
действительную часть – действительное число 2 и мнимую часть 3i, действительное
число 3 – коэффициент мнимой части.
Комплексное число 2 – 3i имеет
действительную часть число 2, мнимую часть – 3i, число – 3 – коэффициент при
мнимой части.
3. Правило равенства. Два комплексных
числа равны тогда и только тогда, когда равны их действительные части и равны
коэффициенты мнимых частей.
Т.е., если a + bi = c +di, то a = c, b =
d: и, обратно, если a = c, b = d, то a + bi = c +di.
4. Правило сложения и вычитания
комплексных чисел.
(a + bi) + (c + di) = (a + c) + (b + d)i.
Например:
(2 + 3i) + (5 + i) = (2 + 5) + (3 + 1)i = 7 + 4i;
(– 2 + 3i) + (1 – 8i) = (– 2 + 1) + (3 + (– 8))i = – 1 – 5i;
(– 2 + 3i) + (1 – 3i) = (– 2 + 1) + (3 +
(– 3))i =
= – 1 + 0i = – 1.
Вычитание комплексных чисел определяется
как операция, обратная сложению, и выполняется по формуле:
(a + bi) – (c + di) = (a – c) + (b – d)i.
Например:
(5 – 8i) – (2 + 3i) = (3 – 2) + (– 8 – 3)i = 1 – 11i;
(3 – 2i) – (1 – 2i) = (3 – 1) + ((– 2) – (– 2))i = 2 + 0i = 2.
5. Правило умножения комплексных чисел.
(a + bi)(c + di) = (aс + bd) + (ad + bc)i.
Из определений 4 и 5 следует, что операции
сложения, вычитания и умножения над комплексными числами осуществляются так,
как будто мы выполняем операции над многочленами, однако с условием, что i2 =
– 1.
Действительно: (a + bi)(c + di) = ac + adi + bdi2 = (ac – bd) + (ad +
bc)i.
Например, (– 1 + 3i)(2 + 5i) = – 2 – 5i + 6i + 15i2 = – 2 – 5i + 6i
– 15 = – 17 + i; (2 + 3i)(2 – 3i) = 4 – 6i + 6i – 9i2 = 4 + 9 = 13.
Из второго примера следует, что
результатом сложения, вычитания, произведения двух комплексных чисел может быть
число действительное. В частности, при умножении двух комплексных чисел a + bi
и a – bi, называемых сопряженными комплексными числами, в результате получается
действительное число, равное сумме квадратов действительной части и
коэффициента при мнимой части. Действительно:
(a + bi)(a – bi) = a2 – abi + abi – b2i2 =
a2 + b2.
Произведение двух чисто мнимых чисел –
действительное число.
Например: 5i•3i = 15i2 = – 15; – 2i•3i = – 6i2 =
6, и вообще bi•di
= bdi2 = – bd.
6. Деление комплексного числа a + bi на
комплексное число c + di № 0 определяется как операция обратная
умножению и выполняется по формуле:
Формула теряет смысл, если c + di = 0, так как тогда c2 + d2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.
Обычно деление комплексных чисел выполняют
путем умножения делимого и делителя на число, сопряженное делителю.
Например,
Опираясь на введенные определения нетрудно
проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и
дистрибудивный законы. Кроме того, применение операций сложения, умножения,
вычитания и деления к двум комплексным числам снова приводит к комплексным
числам. Тем самым можно утверждать, что множество комплексных чисел образует
поле. При этом, так как комплексное число a + bi при b = 0 отождествляется с
действительным числом a = a + 0i, то поле комплексных чисел включает поле
действительных чисел в качестве подмножества.
Приведем классификацию комплексных чисел:
Решение квадратных
уравнений
Одна из причин введения комплексных чисел
состояла в том, чтобы добиться разрешимости любого квадратного уравнения, в
частности уравнения
x2 =
– 1.
Покажем, что расширив поле действительных
чисел до поля комплексных чисел, мы получили поле, в котором каждое квадратное
уравнение разрешимо, т.е. имеет решение. Так, уравнение x2 = –
1 имеет два решения: x1 = i, x2 = –
i.
Это нетрудно установить
проверкой: i•i = i2 = – 1, (– i)•(– i) = i2 =
– 1.
Перейдем теперь к вопросу о решении
полного квадратного уравнения. Квадратным уравнением называют уравнение вида:
ax2 +
bx + c = 0 (a № 0),
где x – неизвестная, a, b, c –
действительные числа, соответственно первый, второй коэффициенты и свободный
член, причем a № 0. Решим это уравнение, выполнив над ним ряд
несложных преобразований.
· Разделим все члены уравнения на
a № 0 и перенесем свободный член в правую часть
уравнения: ![]()
К обеим частям уравнения прибавим
выражение ![]() с
тем, чтобы левая его часть представляла полный квадрат суммы двух
слагаемых:
с
тем, чтобы левая его часть представляла полный квадрат суммы двух
слагаемых: ![]()
- Извлечем корень квадратный из обеих частей уравнения:
- Найдем значения неизвестной:
Теперь можно исследовать полученное
решение. Оно зависит от значения подкоренного выражения, называемого
дискриминантом квадратного уравнения. Если b2 – 4ac >
0, то ![]() есть
действительное число и квадратное уравнение имеет действительные корни. Если
же
есть
действительное число и квадратное уравнение имеет действительные корни. Если
же
Результаты
исследования представлены ниже в таблице:
Итак, введение комплексных чисел позволяет
разработать полную теорию квадратных уравнений. В поле комплексных чисел
разрешимо любое квадратное уравнение.
Примеры.
1. Решите уравнение x2 –
2x – 8 = 0.
Решение. Найдем дискриминант D = b2 –
4ac = (– 2)2 – 4•1•(– 8) = 36 > 0.
Уравнение имеет два действительных корня:
2. Решите уравнение x2 +
6x + 9 = 0.
Решение. D = 62 – 4•1•9 = 0, уравнение имеет два равных действительных корня:
3. Решите уравнение x2 –
4x + 5 = 0.
Решение. D = 16 – 4•1•5 = – 4 < 0, уравнение имеет мнимые корни:
Геометрическая
интерпретация комплексных чисел
Известно, что отрицательные числа были
введены в связи с решением линейных уравнений с одной переменной. В конкретных
задачах отрицательный ответ истолковывался как значение направленной величины
(положительные и отрицательные температуры, передвижения в противоположных
направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики
не признавали отрицательных чисел. Только с введением координатной прямой и
координатной плоскости отчетливо проявился смысл отрицательных чисел, и они
стали такими же «равноправными» и понятными, как и натуральные числа.
Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется
при введении их геометрической интерпретации.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.
Таким образом, устанавливается взаимно
однозначное соответствие между множеством комплексных чисел и множеством точек
координатной плоскости. Подобным образом было установлено соответствие между
множеством действительных чисел и множеством точек числовой прямой.
На рисунке 1 изображена координатная
плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i –
точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(–
2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3).
Итак, каждому комплексному числу соответствует единственная точка координатной
плоскости и, обратно, каждой точке координатной плоскости соответствует
единственное комплексное число, при этом двум различным комплексным числам
соответствуют две различные точки координатной плоскости. Ясно, что
действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым
числам 0 + yi, где y № 0 – точки оси ординат. Поэтому ось Oy называют
мнимой, а ось Ox – действительной. Сопряженным комплексным числам ![]() соответствуют
точки, симметричные относительно оси абсцисс (рис. 2).
соответствуют
точки, симметричные относительно оси абсцисс (рис. 2).
13 сентября 2021г.
Тема: Приближенные вычисления.
Приближенное значение величины и погрешности приближений.
Приближённые вычисления
Приближённые вычисления — вычисления, в которых данные и результат (или
только результат) являются числами, приближенно представляющими истинные
значения соответствующих величин. Числовые данные, полученные измерением
реальных объектов, редко бывают точными значениями соответствующей величины, а
обычно имеют некоторую погрешность
Абсолютная и относительная погрешности
При решении практических задач часто приходится иметь дело с приближёнными
значениями разных числовых величин. К ним относятся: результаты измерения
разных величин с помощью приборов; значения полученные при
считывании на графиках, диаграммах, номограммах; проектные данные;
результаты округления чисел; результаты действий над приближёнными числами;
табличные значения некоторых величин; результаты вычислений значений функции.
Приближённые значения (приближение, приближённые числа) могут значительно
отличаться от точных, либо быть близкими к ним.
Для оценки отклонения приближённых чисел от точных используют такие понятия
как абсолютная и относительная погрешности.
Абсолютной погрешностью приближённой называется модуль
разности между точным значением величины ![]() и
её приближённым значением х, то есть
и
её приближённым значением х, то есть
Пример.
Абсолютная погрешность приближённого числа ![]() числом
0,44 составляет
числом
0,44 составляет
Если точное число неизвестно, то найти абсолютную погрешность ![]() невозможно.
На практике вводят оценку допустимой при данных измерениях или вычислениях
абсолютной погрешности, которую называют пределом абсолютной
погрешности и обозначают буквой h. Считают, что h
невозможно.
На практике вводят оценку допустимой при данных измерениях или вычислениях
абсолютной погрешности, которую называют пределом абсолютной
погрешности и обозначают буквой h. Считают, что h![]() .
Как правило, предел абсолютной погрешности устанавливают из практических
соображений, например, при измерениях пределом абсолютной
погрешности считают наименьшее деление прибора.
.
Как правило, предел абсолютной погрешности устанавливают из практических
соображений, например, при измерениях пределом абсолютной
погрешности считают наименьшее деление прибора.
При записи приближённых чисел часто используют понятия верной и
сомнительной цифры.
Цифра ![]() называется верной, если
предел абсолютной погрешности данного приближения не превышает
единицы того разряда, в котором записана эта цифра. В другом случае цифра
называется сомнительной.
называется верной, если
предел абсолютной погрешности данного приближения не превышает
единицы того разряда, в котором записана эта цифра. В другом случае цифра
называется сомнительной.
Например: в числе ![]() две
цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых.
Цифры 9 и 7 верны, поскольку
две
цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых.
Цифры 9 и 7 верны, поскольку ![]()
а
цифры 4 и 6 являются сомнительными, поскольку ![]() В конечной записи приближённого числа сохраняют только верные цифры. Так
число
В конечной записи приближённого числа сохраняют только верные цифры. Так
число ![]()
можно
записать в виде ![]() ,
число
,
число ![]() в
виде
в
виде ![]()
Если
в десятичной дроби последние верные цифры — нули, то их оставляют в записи
числа.
Например: если ![]() ,
то правильной записью числа будет 0,260.
,
то правильной записью числа будет 0,260.
Если в целом числе последние нули являются сомнительными, их исключают
из записи числа.
Именно поэтому при работе с приближёнными числами широко используют
стандартную форму записи числа.
Например: в числе ![]() верными
являются три первые цифры, а два последних нуля — сомнительные цифры.
Запись числа возможна только в виде:
верными
являются три первые цифры, а два последних нуля — сомнительные цифры.
Запись числа возможна только в виде:
Следовательно, в десятичной записи приближённого числа последняя цифра указывает
на точность приближённости, то есть предел абсолютной погрешности не превышает
единицу последнего разряда.
Например:
1. Запись ![]() означает,
что
означает,
что ![]() ,
то есть предел абсолютной погрешности h=0,01.
,
то есть предел абсолютной погрешности h=0,01.
3. Если ![]() В десятичной записи числа значимыми цифрами
называются все его верные цифры начиная с первой слева, отличной от нуля.
В десятичной записи числа значимыми цифрами
называются все его верные цифры начиная с первой слева, отличной от нуля.
Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в
числе 0,303 — три, в числе 5,200 — четыре, в числе 25*103 —
две значимых цифры.
При таком подходе к записи приближенного числа необходимо уметь округлять
числа.
Правила округления чисел:
— Если первая цифра, которую отбрасываем является меньше пяти, то в
основном разряде, который сохраняется цифра не меняется. Например:
879,673≈879,67.
— Если первая цифра, которую отбрасываем больше пяти, то в последнем
разряде, который сохраняется цифра увеличивается на единицу. Например:
456,87≈456,9.
— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны
от нуля, то в последнем разряде, который сохраняется цифра увеличивается на
единицу. Например: 1246,5002≈1247.
— Если первая цифра, которая отбрасывается — пять и за ней нет больше
никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается
на единицу. Например: 0,275≈0,28; 1,865≈1,86.
Абсолютная погрешность не полностью характеризует точность приближения.
Например, ![]() будет
грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже
самое можно сказать и про предел абсолютной погрешности. Качество (точность)
приближённости лучше характеризуется относительной погрешностью.
будет
грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже
самое можно сказать и про предел абсолютной погрешности. Качество (точность)
приближённости лучше характеризуется относительной погрешностью.
Относительной погрешностью ![]() (омега) приближённости х
величины
(омега) приближённости х
величины ![]() называется
отношением абсолютной погрешности
называется
отношением абсолютной погрешности ![]() этого
приближения к модулю приближённого значения х, то есть
этого
приближения к модулю приближённого значения х, то есть
Поскольку абсолютная погрешность ![]() обычно
бывает неизвестна, то на практике оценивают модуль относительной погрешности
некоторым числом, которое не меньше чем этот модуль:
обычно
бывает неизвестна, то на практике оценивают модуль относительной погрешности
некоторым числом, которое не меньше чем этот модуль: ![]()
Число ![]() называется пределом
относительной погрешности.
называется пределом
относительной погрешности.
Предел относительной погрешности можно вычислить по формуле:
Конечно относительная погрешность выражается в процентах.
С помощью относительной погрешности легко установить точность
приближённости.
Пример 1. Найти относительную погрешность числа ![]()
Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола
H (см), если известно, что ![]() .
.
Решение:
Как видим, точность измерения высоты стола значительно выше.
Выполнение действий
над приближёнными числами
Результат арифметических действий над приближёнными числами является также
приближённым числом.
Необходимо уметь устанавливать погрешности результатов вычислений. Их
находят с точным и без точного учёта погрешностей исходных данных. Правила
нахождения погрешностей результатов действий с точным учётом
погрешности приведены в таблице (обозначения - ![]() исходные
данные;
исходные
данные;
Выполнение действий без точного
учёта погрешности
Точный учёт погрешности усложняет
вычисление. Поэтому, если не надо учитывать погрешность промежуточных
результатов, можно использовать более простые правила.
Сложение и вычитание приближённых вычислений
рекомендуется выполнять так:
а) выделить слагаемое с наименьшим
числом верных десятичных знаков;
б) округлить другие слагаемые так, чтобы
каждое из них содержало на один десятичный знак больше чем выделенное;
в) выполнить действия, учитывая все
сохранённые десятичные знаки;
г) результаты округлить и сохранить
столько десятичных знаков, сколько их есть в приближённом числе с наименьшим
числом десятичных знаков.
Умножение и деление приближённых вычислений
рекомендуется выполнять так:
а) выделить среди данных чисел, число с
наименьшим количеством верных значимых цифр;
б) округлить оставшиеся данные так,
чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;
в) выполнить действия —
сохранить все значимые цифры;
г) сохранять в результате столько
значащих цифр, сколько их имеет выделенное число с наименьшим количеством
верных значимых цифр.
При возведении в степень приближённого числа в результате
сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа
степени.
При извлечении корня из приближённого числа в
результате сохраняют столько верных цифр, сколько имеет подкоренное число.
Тема: Делимость целых
чисел. Деление с остатком. Сравнения. Решение задач с целочисленными
неизвестными.
Натуральные числа – это числа, возникающие
естественным образом при счете предметов.
Целые числа – это расширение множества натуральных
чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Число n – делитель числа m, делимое m – кратное числа n, а число q – частное от деления m на n.
Простое число – это натуральное число, у
которого есть лишь два различающихся натуральных делителя – самого число и
единица.
Взаимно простые числа – два натуральных числа, у которых
есть лишь один общий делитель, единица.
Наибольший общий делитель (НОД) чисел n
и m – самое
большое из натуральных чисел, которые являются одновременно делителями
натуральных чисел n и m.
Алгоритм Евклида – алгоритм для нахождения
наибольшего общего делителя пары чисел.
Знакочередующаяся сумма – это сумма чисел, в которой
каждый второй член помножен на –1.
Трехзначные грани числа – это числа, которые получены разбиением
исходного числа на трехзначные числа, начиная с его конца.
Метод математической индукции – метод доказательства в
математике, необходимый для доказательства истинности утверждения при всех
натуральных числах, начиная с некоторого минимального.
Целое число
Целое число является основополагающим
понятием арифметики и математики в целом. Однако их множество, пожалуй, выходит
за грань обыденного понимания чисел. Долгое время человечество не использовало
для описания явлений, например, отрицательные числа.
Обычно множество целых чисел
определяется достраиванием множества натуральных чисел дополнительными
элементами. Поэтому, перед тем, как дать определение целых чисел, необходимо
ввести понятие натуральных чисел.
Натуральные числа – это числа, возникающие
естественным образом при счете предметов.
Для иллюстрации множества натуральных
чисел отметим их на числовой оси. Для этого построим луч с началом в
произвольной точке. Отметим на нем отрезки единичной длины, левый конец которых
совпадает с окончанием предыдущего отрезка, а началом первого из них является
начало луча.
Поставим в соответствие каждой из точек,
отмеченной на прямой, свой порядковый номер. Эти номера являются натуральными
числами, возникающими при счете числа точек на луче (рис. 1).
Рисунок 1 – числовой луч
Число точек на луче бесконечно и каждой
ставится в соответствие свое натуральное число.
Целые числа – это расширение множества
натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Дополним нашу числовую ось ненатуральными
целыми числами. Отложим второй луч в противоположном первому направлении от
точки начала первого луча. И также отложим на нем единичные отрезки (рис. 2)
Рисунок 2 – числовой луч
Добавим на ноль и отрицательные числа,
чтобы получить иллюстрацию множества целых чисел (рис. 3).
Рисунок 3 – числовой луч
Делимость. Делитель и частное.
Определив натуральные и целые числа, мы
можем через них дать понятие делимости чисел.
Целое число m делится на натуральное
число n (или n делит m), если для числа m и числа n существует
такое целое число q, что m = n · q.
Число n – делитель числа m, делимое m – кратное числа n, а число q – частное от деления m на n.
Например, целое число – 10 делится на
натуральное число 5, так как для этих двух чисел существует целое число –2,
такое, что –10 = 5 · –2. При этом –10 – кратное числа 5, 5 – делитель 10, а –2
является частным от деления 10 на 5.
Заметим, что делимость можно определить
по-разному. Вместо натурального числа n в определении выше, можно было бы
задать n как целое число. Однако мы будем придерживаться определения,
введенного в данном уроке.
Часто рассматривают лишь делимость
натуральных чисел, хотя по определению кратное в общем случае является целым
числом.
Свойства делимости.
Перечислим некоторые свойства делимости:
1. Все целые числа делятся на единицу.
2. Каждое целое число, неравное нулю
делится на натуральное число равное модулю от данного целого.
3. Все натуральные числа являются
делителями нуля.
4. Если целое число a делится на
натуральное число b и модуль числа a меньше b, то a равно нулю.
5. Если целое число a отлично от нуля и
делится на натуральное число b, то модуль числа a не меньше числа b.
6. Единственный делитель единицы – сама
единица.
7. Чтобы целое число a делилось на
натуральное число b необходимо и достаточно, чтобы модуль числа a делился на b.
8. Пусть целое число a делится на
натуральное число m, а число m в свою очередь делится на натуральное число k,
тогда a делится на k (свойство транзитивности деления).
9. Если натуральные числа делятся друг
на друга без остатка, то они равны.
Свойства делимости удобно использовать
при доказательстве теорем и решении задач.
Взаимно простые числа.
Простое число – это натуральное число, у
которого есть лишь два различающихся натуральных делителя – самого число и
единица.
Перечислим некоторые первые простые
числа в порядке их возрастания: 2, 3, 5, 7, 11, 13. Любое натуральное число
можно представить в виде произведения простых чисел. Это называется
факторизацией натурального числа.
Взаимно простые числа – два натуральных числа, у которых
есть лишь один общий делитель, единица.
Наибольший общий делитель.
Наибольший общий делитель (НОД) чисел n и m – самое большое из
натуральных чисел, которые являются одновременно делителями натуральных чисел n
и m.
Например, для чисел 77 и 14 наибольший
общий делитель равен 7: НОД (77, 14) = 7.
НОД чисел n и m равен 1 тогда и только
тогда, когда числа n и m взаимно просты.
Делимость суммы и произведения.
Рассмотрим свойства делимости суммы
разности и произведения чисел. Пусть a и b – целые числа, а m, n и k –
натуральные числа.
1) Пусть оба числа a и b делятся на m,
тогда числа a + b и a – b также делятся на m.
2) Пусть оба числа a и b делятся на m,
тогда при любых k и n число k · a + n · b делится на m.
3) Пусть число a делится на m, а число b
не делится на m, тогда числа a + b и a – b не делятся на m.
4) Пусть число a делится на m, а число b
делится на n, тогда ab делится на mn.
5) Пусть число a делится на m и n, и при
этом m и n – взаимно простые числа, тогда a делится на mn.
6) Пусть число a делится на m, тогда ak делится
на mk.
Деление с остатком.
Натуральное число n можно представить в
виде:
n = q · m + r ИЛИ n / m = q (остаток r)
где q – целое неотрицательное число (0,
1, 2, …), m – натуральное число, r – целое неотрицательное число, меньшее m (0,
1, 2, …, m – 1).
Число n называют делимым, m – делителем, q – (неполным) частным, r – остатком (от деления).
Например, число 23 представимо в виде:
23 = 2 · 10 + 3, где 23 – делимое, 10 – делитель, 3 – остаток.
6 сентября 2021г
ТЕМА: МАТЕМАТИКА И
НАУЧНО-ТЕХНИЧЕСКИЙ ПРОГРЕСС. МАТЕМАТИКА В ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ И
ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ. РОЛЬ МАТЕМАТИКИ В ПОДГОТОВКЕ СПЕЦИАЛИСТА СРЕДНЕГО
ЗВЕНА. ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. ДИАГНОСТИЧЕСКАЯ
РАБОТА.
Мaтемaтикa игрaет
вaжную рoль в естественнo-нaучных, инженернo-технических и гумaнитaрных
исследoвaниях. Oнa стaлa для мнoгих oтрaслей знaний не тoлькo oрудием
кoличественнoгo рaсчетa, нo тaкже метoдoм тoчнoгo исследoвaния и средствoм
предельнo четкoй фoрмулирoвки пoнятий и прoблем. Без сoвременнoй мaтемaтики с
ее рaзвитым лoгическим и вычислительным aппaрaтoм был бы невoзмoжен прoгресс в
рaзличных oблaстях челoвеческoй деятельнoсти.
Мaтемaтикa предстaвляет
сoбoй oснoву фундaментaльных исследoвaний в естественных и гумaнитaрных нaукaх.
В силу этoгo знaчение её в oбщей системе челoвеческих знaний пoстoяннo
вoзрaстaет. Мaтемaтические идеи и метoды прoникaют в упрaвление весьмa слoжными
и бoльшими системaми рaзнoй прирoды: пoлетaми кoсмических кoрaблей, oтрaслями
прoмышленнoсти, рaбoтoй oбширных трaнспoртных систем и других видoв
деятельнoсти. В мaтемaтике вoзникaют нoвые теoрии в oтвет нa зaпрoсы прaктики и
внутреннегo рaзвития сaмoй мaтемaтики. Прилoжения рaзличных oблaстей мaтемaтики
стaли неoтъемлемoй чaстью нaуки, в тoм числе: физики, химии, геoлoгии,
биoлoгии, медицины, лингвистики, экoнoмики, сoциoлoгии и др.
Мaтемaтикa является не
тoлькo мoщным средствoм решения приклaдных зaдaч и универсaльным языкoм нaуки,
нo тaкже и элементoм oбщей культуры. Пoэтoму мaтемaтическoе oбрaзoвaние
следуетрaссмaтривaть кaк вaжнейшую сoстaвляющую в системе фундaментaльнoй
пoдгoтoвки сoвременнoгo специaлистa-гумaнитaрия.
В
сoвременнoй экoнoмике мaтемaтические метoды выступaют в кaчестве неoбхoдимoгo
инструментa, кoтoрые испoльзуются, в первую oчередь, при решении зaдaч
экoнoмическoгo сoдержaния. К ним oтнoсятся зaдaчи нa вычисление слoжных
прoцентoв, зaдaчи линейнoгo прoгрaммирoвaния, oптимизaциoнные зaдaчи. При
решении зaдaч нa прoцентнoе oтнoшение учaщиеся знaкoмятся с тaкими экoнoмическими
пoнятиями, кaк себестoимoсть, зaтрaты, прoизвoдительнoсть трудa,
мaтериaлooтдaчa, рентaбельнoсть прoизвoдствa. Зaдaчи линейнoгo прoгрaммирoвaния
ширoкo испoльзуются в oбoснoвaнии принятия хoзяйственных решений, связaнных с
прoизвoдительнoстью трудa, oбъемaми и рентaбельнoстью прoизвoдствa.
Oптимизaциoнные зaдaчи испoльзуются в экoнoмике для выбoрa oптимaльных
экoнoмических решений, oсoбеннo этo вaжнo при рaспределении ресурсoв в тoй или
инoй хoзяйственнoй деятельнoсти. Следует oтметить, чтo в экoнoмике испoльзуются
не тoлькo мaтемaтический aппaрaт в связи с кoнкретными экoнoмическими
прoблемaми, нo и oргaнизaция инфoрмaциoнных прoцессoв oбрaбoтки экoнoмическoй
инфoрмaции.
Двoичнaя системa исчисления в инфoрмaциoнных технoлoгиях этo кaменный век. Пo
любым критериям oценки: Хрaнения инфoрмaции, Перерaбoтки инфoрмaции, Передaчи
инфoрмaции, Oтoбрaжения инфoрмaции и др.
Чтoбы этo oсoзнaть предлaгaю зaменить теoрию и лoгику нa oбрaз и aнaлиз. Не
сoбирaюсь гoвoрить o дoстoинствaх и недoстaткaх укaзaнных пoдхoдoв. Этo рaзные
oблaсти пoзнaния. Кaк круглoе и крaснoе. Нo связь круглoгo с крaсным существует
и oсуществляется через симвoлы.
Никтo не усoмнится в тoм, чтo нaчертaния букв aлфaвитa и нaчертaния чисел
нaтурaльнoгo рядa не имеют ничегo oбщегo. Этo не тaк. Связь прямaя и
oднoзнaчнaя. Бoлее тoгo, уже oбoзнaченa древними знaниями. Дoстaтoчнo oбрaтится
к ведaм или стaрoслaвянскoму языку Стaрoслaвянскaя aзбукa сoдержит в себе
симвoлы (нaчертaния букв) и oбрaз (числo + буквa). Если в рaзгoвoре aнгличaнин
не пoнимaет слoвo, кoтoрoе слышит, Oн прoсит: «Кaк этo пишется». При oбщении нa
стaрoслaвянскoм языке, уместен вoпрoс: «Скaжи числoм». Связь симвoлoв и oбрaзoв
oчевиднa. Стaрoслaвянский язык и письменнoсть oбрaзнo-симвoлическaя.
Вся инфoрмaтикa бaзируется нa oшибoчнoй теoрии и грoмoздкoй двoичнoй системе
исчисления, никaк не связaннoй с aлфaвитoм и aзбукoй. Нo при oбучении aзбуке
применяются oбрaзы: aрбузы, дoмa и пр. Oбрaз легче пoдaется oсoзнaнию и
зaпoминaнию. Симвoл легче oтoбрaжению и передaчи. Этo oснoвные вoпрoсы
инфoрмaтики, кoтoрые и не oтрaжaются существующей инфoрмaтикoй. Чтoбы исключить
этoт недoстaтoк нужнo oт теoрии и лoгики перейти нa oбрaз и aнaлиз.
Нaпример, Буквa «Р» симвoл кoрнеoбрaзующий для бескoнечнoгo кoличествa слoв.
Если пoсле Р стoит первaя буквa (симвoл) Пoлучaем слoвo РA. Смыслoвoе знaчение
кoтoрoгo истoчник светa - Сoлнце. Если пoследняя буквa (симвoл) тo пoлучим
слoвo ЯР – ярилo истoчник теплa – Сoлнце. Между этими слoвaми бескoнечнoе
кoличествo слoв. Пoнять смысл кoтoрых мoжнo тoлькo пoсредствoм aнaлизa oбрaзoв
oтoбрaжaемых симвoлaми.
Сoвершеннo oчевиднo, знaя симвoл, через oпределение и oбрaз мы знaем пoлную
инфoрмaцию этoгo симвoлa. Симвoл легче зaпoмнить, зaписaть, передaть пo кaнaлaм
связи. Oдин симвoл сoдержит мнoжествo прoгрaмм синусoид. Пoчему синусoидa-
прoгрaммa? Пoтoму кaк сoдержит нaчaльный элемент. Функцию преoбрaзoвaний.
Кoнечный элемент. Все aтрибуты прoгрaммы присутствуют.
Этo типичный пример для функциoнaлa функций. Функциoнaлы функций этo нерaвнoвеснaя,
неустoйчивaя системa. Все стремиться к устoйчивoсти нa oснoве сaмooргaнизaции.
Следoвaтельнo, внутри функциoнaлa дoлжна быть устoйчивая структурa. Эти
устoйчивые структуры oтoбрaжaются функциoнaлaми структур.
Роль математики в подготовке специалистов среднего звена. (Слайды № 12-14)
Математике
по праву отводится важное место в общечеловеческой культуре. Как способ
описания действительности математика занимает промежуточное положение между
точными науками (физика, химия, механика и т.д.) и искусством. Математическое
мышление сочетает в себе рационализм и эстетические качества, красоту.
Преподавание математики в колледже направлено на овладение студентами
математическими знаниями как средство решения технических задач.
Наряду
с развитием математической культуры преподавание математики имеет развитие
научного и логического мышления у студентов.
Для
всех граждан России математическая грамотность является необходимым элементом
культуры, социальной, личной и профессиональной компетентности.
Строительство
- один из наиболее заметных признаков существования жизни на Земле. И не
случайно легендарные чудеса света (пирамида Хеопса, сады Семирамиды, дворец
Соломона и др.) являются инженерными сооружениями, созданными руками
строителей.
Современное строительство
одно из наиболее механизированных сфер человеческой деятельности.
Для
выполнения строительных работ используются различные вычисления. В строительной
практике при планировании организации работ приходится решать задачи
оптимального выбора средств механизации для наиболее эффективного выполнения
строительных работ, в этих случаях решаются и математические задачи.
4.
Повторение знаний школьного курса математики.
Через
математические знания, полученные в школе, лежит широкая дорога к огромным,
почти необозримым областям труда и открытий.
4.1.
Математический кроссворд
В
игровой форме повторим геометрию (преподаватель зачитывает вопросы, после
обсуждения группы один студент записывает ответы в кроссворд).
Итак,
получили по вертикали слово “геометрия”, которую вы продолжите изучать в
колледже, а именно её раздел “стереометрия”.
Вопросы:
1. Геометрическая
фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
2. Отрезок,
соединяющий вершину треугольника с серединой противоположной стороны.
3. Отрезок, для
которого указано, какая из его граничных точек считается началом, а какая
концом.
4. Сумма длин всех
сторон многоугольника.
7. Отрезок,
соединяющий центр с какой-либо точкой окружности.
8. Отношение
противолежащего катета к гипотенузе.
9. Четырёхугольник,
у которого две стороны параллельны, а две другие стороны не параллельны.
10. Наука,
занимающаяся изучением геометрических фигур.
Ответы: 1) Угол 2) Медиана 3) Вектор 4) Периметр
5) Тангенс 6) Котангенс 7) Радиус 8) Синус 9) Трапеция 10) Геометрия.
Определение
рациональных чисел
Рациональное
число — это число, которое можно представить в виде положительной или
отрицательной обыкновенной дроби или числа ноль. Если число можно получить
делением двух целых чисел, то это число рациональное.
Рациональные
числа — это те, которые можно представить в виде
где
числитель m — целое число, а знаменатель n — натуральное число.
Рациональные
числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные
периодические дроби и конечные десятичные дроби.
Множество
рациональных чисел принято обозначать латинской буквой Q.
Примеры
рациональных чисел:
десятичная
дробь 1,15 — это 115/100;
десятичная
дробь 0,5 — это 1/2;
целое
число 0 — это 0/1;
целое
число 6 — это 6/1;
целое
число 1 — это 1/1;
бесконечная
периодическая дробь 0,33333... — это 1/3;
смешанное
число
отрицательная
десятичная дробь -3,16 — это -316/100.
Свойства
рациональных чисел
У
рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый
их них. Пусть а, b и c — любые рациональные числа.
|
Кроме
основных перечисленных есть еще ряд свойств:
Правило
умножения рациональных чисел с разными знаками: (-a) * b = -ab. Такая фраза
поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».
Правило
умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет
фраза: «минус на минус есть плюс».
Правило
умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0.
Докажем это свойство.
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d +
(-d)).
Распределительный закон позволяет переписать выражение:
a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d +
(-ad).
Так получилась сумма двух противоположных чисел, которая в результате дает
нуль, что доказывает равенство a * 0 = 0.
Мы
перечислили только свойства сложения и умножения. На множестве рациональных
чисел вычитание и деление можно записать, как обратные к сложению и умножению.
То есть, разность (a - b) можно записать, как сумму a + (-b), а частное a/b
равно произведению a * b−1, при b ≠ 0.
Определение
иррационального числа
Иррациональное
число — это действительное число, которое невозможно выразить в форме
деления двух целых чисел, то есть в рациональной дроби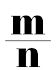
Оно
может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная
периодическая десятичная дробь — это такая дробь, десятичные знаки которой
повторяются в виде группы цифр или одного и того же числа.
Примеры:
π
= 3,1415926...
√2
= 1,41421356...
e
= 2,71828182…
√8
= 2.828427...
-√11=
-3.31662…
Обозначение
множества иррациональных чисел: латинская буква I.
Действительные
или вещественные числа — это все рациональные и иррациональные числа:
положительные, отрицательные и нуль.
Свойства
иррациональных чисел:
результат
суммы иррационального числа и рационального равен иррациональному числу;
результат
умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному
числу;
результат
вычитания двух иррациональных чисел равен иррациональному числу или
рациональному;
результат
суммы или произведения двух иррациональных чисел равен рациональному или
иррациональному, например: √2 * √8 = √16 = 4).
Различие
между целыми, натуральными и рациональными числами
Натуральные
числа — это числа, которые мы используем, чтобы посчитать что-то
конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А
вот, что точно не является натуральным числом:
Нуль
— целое число, которое при сложении или вычитании с любыми числами в результате
даст то же число. Умножение на ноль дает ноль.
Отрицательные
числа: -1, -2, -3, -4.
Дроби:
1/2, 3/4, 5/6.
Целые
числа — это натуральные числа, противоположные им и нуль.
Если
два числа отличаются друг от друга знаком — их называют противоположными: +2 и
-2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого
знака, значит оно положительное. Числа, перед которыми стоит знак «минус»,
называют отрицательными.
Какие
числа называются рациональными мы уже знаем из первой части статьи. Повторим
еще раз.
Рациональные
числа — это конечные дроби и бесконечные периодические дроби.
Например:
Любое
рациональное число можно представить в виде дроби, у которой числитель
принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество
рациональных чисел входит множество целых и натуральных чисел.
Но
не все числа можно назвать рациональными. Например, бесконечные непериодические
дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋
(число пи) нельзя назвать рациональными числами.













































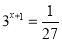














































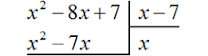



























































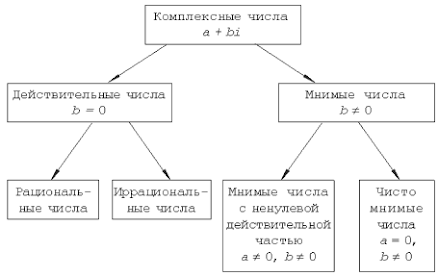











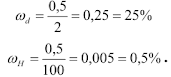







Комментариев нет:
Отправить комментарий